辅导班签到表(竖版)备课讲稿.doc 3页

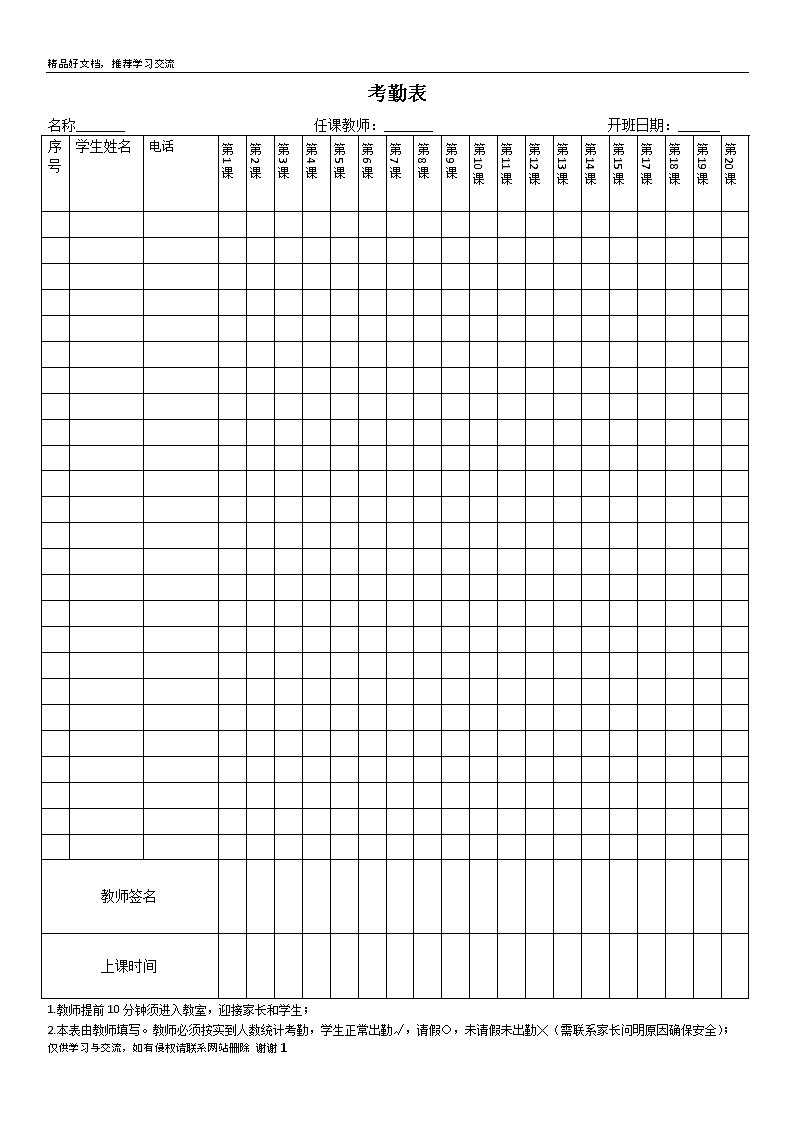
'精品好文档，推荐学习交流考勤表名称_______任课教师：_______开班日期：______序号学生姓名电话第1课第2课第3课第4课第5课第6课第7课第8课第9课第10课第11课第12课第13课第14课第15课第17课第18课第19课第20课教师签名上课时间1.教师提前10分钟须进入教室，迎接家长和学生；2.本表由教师填写。教师必须按实到人数统计考勤，学生正常出勤√，请假○，未请假未出勤╳（需联系家长问明原因确保安全）；仅供学习与交流，如有侵权请联系网站删除谢谢3 精品好文档，推荐学习交流3.教师必须严格按照课时排配进度授课，不要拖后或提前；4.教师必须在倒数第5次课协助学校做好升班续费工作，班级升班率至少达到80%以上。初等代数研究课后习题20071115033数学院07（1）杨明1、证明自然数的顺序关系具有对逆性与全序性，即（1）对任何，当且仅当时，.（2））对任何，在，，中有且只有一个成立.证明：对任何，设，（1）“”，则,使，,“”，则,使，,综上对任何，（2）由（1）与不可能同时成立，假设与同时成立，则,使且，与B为有限集矛盾，与不可能同时成立，综上，对任何，在，，中有且只有一个成立..2、证明自然数的加法满足交换律.证明：对任何设M为使等式成立的所有b组成的集合先证，设满足此式的组成集合k，显然有1+1=1+1成立，设，，则，，取定，则，设，则对任何，3、证明自然数的乘法是唯一存在的证明：唯一性：取定，反证：假设至少有两个对应关系，对，有，设是由使成立的所有的组成的集合，设则，，即，仅供学习与交流，如有侵权请联系网站删除谢谢3 精品好文档，推荐学习交流仅供学习与交流，如有侵权请联系网站删除谢谢3'