管理运筹学教学课件PPT存储论.ppt 43页

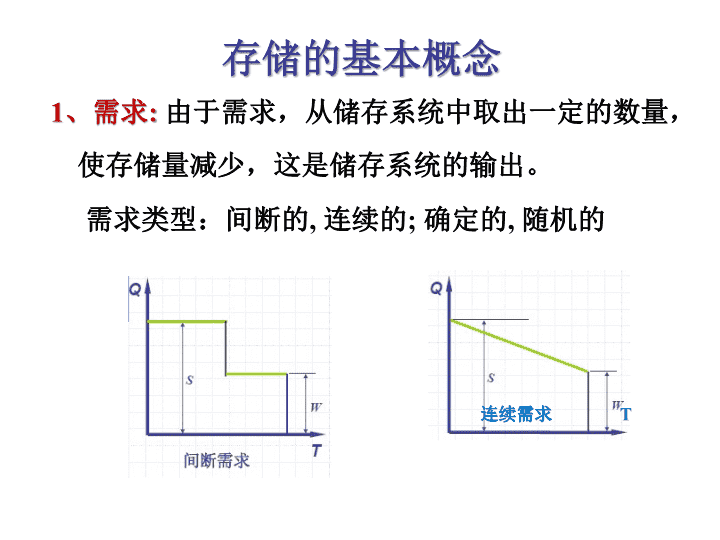
'第十三章存储论§1经济订购批量存储模型§2经济生产批量模型§3允许缺货的经济订购批量模型§4允许缺货的经济生产批量模型§5经济订购批量折扣模型§6需求为随机的单一周期的存储模型§7需求为随机的订货批量、再订货点模型 1915年，哈里森提出最佳订购批量公式，随后威尔逊推广应用。20世纪40年代后，人们日益重视库存问题，因为库存构成了企事业单位收支平衡中显著的部分，一些公司由于缺乏对库存量的控制而失败，从而促使存储理论的发展，运筹学增添了一个分支—存储论。一般来说，货物保管一年所需的全部费用大约是或物价格的20%左右（包括资金利息），超量的库存占用大量的流动资金，使流动资金冻结于停滞的存储环节，是现代企业家所忌讳的，现代企业管理追求“零库存”。 存储的基本概念1、需求:由于需求，从储存系统中取出一定的数量，使存储量减少，这是储存系统的输出。需求类型：间断的,连续的;确定的,随机的需求连续需求T 存储的基本概念2、补充(订货和生产)由于需求增加，存储量必须加以补充，这是存储的输入（订货或自行生产）批量：每一批补充数量周期：两次补充之间的时间提前期：(拖后期):补充存储的时间 3、存储总费用构成存储费=单位存储费×库存量：资金利息、仓库保管，储存物资变质损失订货费=每次订货费×订货次数：每次订货的手续费、电话费、出差费等生产准备费=每次生产准备费×生产次数：每次生产的准备、结束费货物成本费=货物价格×需求量：货物本身价格，或是与产品数量相关的可变费用缺货费=单位缺货费×缺货量：缺货损失，停工待料或未履行合同罚款。 年需求量D为常数当存储降至零时，可以得到立即补充；不允许缺货；订货批量Q；每次订货费为c3，单位物资单位时间的存储费为c1。各种参数（D、c3、c1）均为常数§1经济订购批量存储模型经济订货批量Q*(EOQ--EconomicOrderQuantity)模型假设 t0QR时间库存量Q’物资耗用速率R为单位时间内的库存耗用量。一个周期t内的耗用量Rt数值上等于周期开始时的库存量Q，即Q=Rt。§1经济订购批量存储模型 一个周期内的平均库存量为：设t´时刻的库存量为Q´，有Q´=Q-Rt´，则一个周期t内的总库存量为一年内的总费用=存储费+订货费+货物成本费求极小值§1经济订购批量存储模型 求极值得使总费用最小订购批量为这是经济订购批量公式，也称哈里森-威尔逊公式。单位时间内的存储费用=单位时间内的订货费用=§1经济订购批量存储模型 周123456789101112总计平均每周需求（箱）30003080296029502990300030203000298030303000299036003000§1经济订购批量存储模型例1.益民食品批发部是个中型的批发公司，它为附近200多家食品零售店提供货源。批发部的负责人为了减少存储的成本，他选择了某种品牌的方便面进行调查研究，制定正确的存储策略。下面为过去12周的该品牌方便面的需求数据。 §1经济订购批量存储模型 §1经济订购批量存储模型订货周期T0=一年的总费用 经济生产批量模型也称不允许缺货、边生产边消耗模型，这也是一种确定型的存储模型。它的存储状态如上图。存储量时间t生产时间不生产时间平均存储量最高存储量p-dd§2经济生产批量模型 这种存储模型的假设：1.需求率（单位时间的需求量）为d2.生产率（单位时间的产量）为p，生产量为Q；3.不允许缺货；4.单位产品单位时间的存储费c1；5.每次的生产准备费c3；6.每期初进行补充。不能得到立即补充，生产需一定时间。§2经济生产批量模型 生产时间：最高存储量：平均存储量：一年存储费：一年的生产准备费用:一年的总费用TC为：§2经济生产批量模型 使TC达最小值的最佳生产量每个周期所需时间为时，经济生产批量模型趋于经济订购批量模型。§2经济生产批量模型 例1.有一生产和销售图书馆设备的公司，经营一种图书馆专用书架，预测估计该书架今年一年的需求量为4900个。存储一个书架一年的费用为1000元。这种书架的生产能力为每年9800个，组织一次生产的费用为500元。为了降低成本，该公司如何组织生产？要求求出最优的生产量，相应的周期，最少的年度费用，每年的生产次数。解：从题可知，年需求量D=4900，年需求率d=4900.年生产率p=9800,c1=1000,c3=500，代入公式可得§2经济生产批量模型 §2经济生产批量模型 这种模型的存储状态图为：时间存储量oSQ-S最大缺货量最大存储量T不缺货时间t1缺货时间t2§3允许缺货的经济订购批量模型 这种存储模型的假设：1.需求率（单位时间的需求量）为d；2.允许缺货，且最大缺货量为S；3.单位货物单位时间的存储费c1；4.每次的订货费c3；5.单位时间缺少一个单位货物所支付缺货费c2；6.当缺货量达到S时进行补充，且很快补充到最大存储量。§3允许缺货的经济订购批量模型 平均存储量=周期总存储量/周期时间=（不缺货时的存储量+缺货时的存储量）/周期时间不缺货的时间:总周期时间：把后两个公式代入第一个公式得到：§3允许缺货的经济订购批量模型 平均缺货量：周期中的缺货时间：一年总费用=存储费+订货费+缺货损失费§3允许缺货的经济订购批量模型 对TC求偏导数：最优订货量：最大缺货量：§3允许缺货的经济订购批量模型 例2：假设例1中图书馆设备公司不生产书架，只销售书架。其销售的书架靠订货提供而且都能及时供货。该公司一年的需求量为4900个，一个书架一年的存储费用为1000元，每次订货费为500元，每年的工作日为250天。允许缺货，设一个书架缺货一年的缺货费为2000元。求一年总费用最低的最优每次订货量及相应的周期，相应的最大缺货量，同期中缺货的时间，不缺货的时间，每年的订购次数，一年的总费用。§3允许缺货的经济订购批量模型 解：最优订购批量最大缺货量为周期所需时间周期缺货时间§3允许缺货的经济订购批量模型 周期中不缺货时间为每年订购次数为年度总费用§3允许缺货的经济订购批量模型 此模型与经济生产批量模型相比，放宽了假设条件：允许缺货。这种模型的存储状态图为：此模型与经济生产批量模型相比，放宽了假设条件：允许缺货。这种模型的存储状态图为：时间OSV最大缺货量最大存储量Tt1t2t3t4p-dd§4允许缺货的经济生产批量模型 所谓货物单价有“折扣”是指供应方采取的一种鼓励用户多订货的优惠政策，即根据订货量的大小规定不同的货物单价。如所谓零售价、批发价和出厂价。因为不同订货量，单价不同，导致总费用也不同。因此，在订货批量的模型中总费用可以由三项构成，即有式中p为当订货量为Q时的单位货物的单价。§5经济订货批量折扣模型 例4.图书馆设备公司从厂家购进阅览桌用于销售，每个阅览桌500元，每个阅览桌存储一年的费用为阅览桌价格的20%，每次订货费200元，预测这种阅览桌每年需求300个。厂商为了促销规定：如果一次订购量达到或超过50个，每个阅览桌为480元；如达到或超100个，售价475元。请决定最优订货批量.解：已知D=300个/年，c3=200/次Q<50时，p1=500元，c1‘=500*20%=100（元/个年）50≤Q<100时，p2=480元，c1‘’=480*20%=96（元/个年）100≤Q时，p3=475元，c1‘’‘=475*20%=95（元/个年）§5经济订货批量折扣模型 Q<50时，50≤Q<100时，100≤Q时，§5经济订货批量折扣模型TC是关于Q的分段函数。由微积分知识可知，TC的最小值只可能在函数导数不存在的点、区间的端点和驻点达到。 §5经济订货批量折扣模型（为驻点）（为区间端点）（为区间端点）比较上面三个数值，得一年的总费用最少为147600元，因此，最佳订货批量为Q＊=50。计算TC得 报童问题：报童每天销售报纸的数量是一个随机变量，每日售出d份报纸的概率P(d)(根据以往的经验)是已知的。报童每售出一份报纸赚k元，如果报纸未能售出，每份赔h元，问报童每日最好准备多少报纸？如果订货量Q选得过大，那么报童就会因不能售出报纸造成损失；如果订货量Q选得过小，那么报童就要因缺货失去销售机会而造成机会损失。§6需求为随机的单一周期存储模型 解：已知报童售出d份报纸的概率为P(d),由概率论知又知报童因报纸未能售出而造成每份损失h元，因缺货而造成机会损失每份k元，则当订货量为Q时，其上述两项损失的期望值之和EL为其中前一项是供大于求时(Q≥d)报童因报纸未能售出而造成损失的期望值；后一项是供不应求时(Q≤d)报童因缺货而造成机会损失的期望值。§6需求为随机的单一周期存储模型 设报童订购报纸的最优量为Q＊，这时其两种损失的期望值之和为最小，即Q＊应满足(1)EL(Q＊)≤EL(Q＊+1)(2)EL(Q＊)≤EL(Q＊-1)从(1)式有§6需求为随机的单一周期存储模型 化简得即从(2)式有化简得§6需求为随机的单一周期存储模型 即由(1)、(2)两式推导出满足下面不等式的Q＊是这两种损失的期望值之和最小的订报量§6需求为随机的单一周期存储模型 例5.某报亭出售某种报纸，每售出一百张可获利15元，如果当天不能售出，每一百张赔20元。每日售出该报纸份数的概率P(d)根据以往经验如下表所示。试问报亭每日订购多少张该种报纸能使其赚钱的期望值最大。销售量（百张）567891011概率P(d)0.050.100.200.20.250.150.05§6需求为随机的单一周期存储模型 解：要使其赚钱的期望值最大，也就是使其因售不出报纸的损失和因缺货失去销售机会的损失的期望值之和为最小。有另有故当Q=8时，不等式成立.因此,最优订报量为每天800张。（不断尝试）§6需求为随机的单一周期存储模型 §6需求为随机的单一周期存储模型把公式改写成公式（13.43）既适用于离散型随机变量也适用于连续型随机变量。如果只考虑连续型随机变量，公式（13.43）又可以改写为 例6.某书店拟在年前出售一批新年挂历。每本可盈利20元，如年前不能售出，必须削价处理,每本挂历要赔16元。根据经验，市场需求量服从均匀分布，最低需求550本，最高需求1100本，该书店应订购多少新年挂历，使损失期望值为最小？解：由题意知挂历服从区间[550，1100]分布，k=20，h=16，则其需求量小于Q＊的概率为则由公式（13.44）得由此求得Q＊=856（本），并从5/9可知，这时有5/9的概率挂历有剩余。§6需求为随机的单一周期存储模型 由于需求为随机变量，无法求得周期和订货点。下面给出最优解的近似方法。具体求解步骤如下：1.设全年的需求量近似为D，利用经济订货批量存储模型求出（每次的）最优订货量Q＊。2.制定出服务水平，即制定m天里出现缺货的概率，也即不出现缺货概率为1。利用下式求订货点rP(m天里需求量r)=1存储的(r，Q)策略r为最低存储量，即订货点。对库存量H随时进行检查，当H>r时不补充；当H≤r时进行补充，每次补充的数量为Q。§7需求为随机的订货批量、订货点模型 例8.某装修材料公司经营某品牌地砖，直接从厂家进货。由于与厂家较远，合同规定，在填写订货单后一个星期，厂家把地砖运到公司。根据以往的数据统计分析，在一个星期里此种地砖的需求量服从以均值=850箱，方差=120箱的正态分布。每次订货费为250元，每箱地砖成本48元，存储一年的存储费用为成本的20%。公司规定的服务水平为允许由于存储量不够造成的缺货情况为5%。公司应如何制定存储策略，使得一年的总费用为最少？解：首先求出最优订货批量Q＊。已知每年的平均需求量D=850×52=44200箱/年，c1=9.6元/箱年，c3=250元，得§7需求为随机的订货批量、订货点模型 每年约订货44200/1517≈29次。由服务水平，得P(一个星期的需求量r)=1=10.05=0.95进一步，有查标准正态分布表，得进一步，有r=1047。安全存储量（防止缺货）为r=1047850=197箱。这样的存储策略下，在订货期有95%的概率不会缺货。§7需求为随机的订货批量、订货点模型'