数学：2.3《解三角形的实际应用举例-三角函数模型的应用》课件PPT(北师大版必修5).ppt 18页

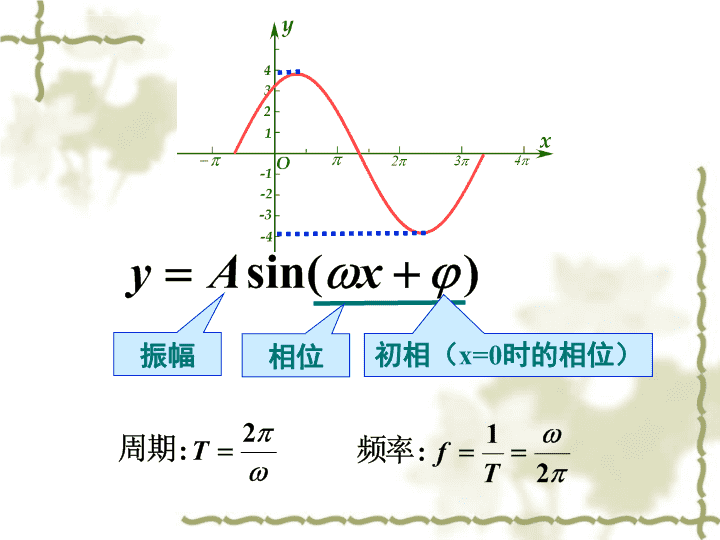
'数学：２．３《解三角形的实际应用举例－三角函数模型的应用》课件PPT（北师大版必修5） 三角函数模型的简单应用 振幅初相（x=0时的相位）相位 例1．如图：点O为作简谐运动的物体的平衡位置，取向右的方向为物体位移的正方向，若已知振幅为3cm，周期为3s，且物体向右运动到距离平衡位置最远时开始计时。（1）求物体对平衡位置的位移x（cm）和时间t(s)之间的函数关系；（2）求物体在t=5s时的位置。 例2．如图：一个半径为3m的水轮，水轮圆心O恰在水面上，已知水轮每分钟转动4圈，水轮上点P在下列位置开始计时。（1）将点P距离水面的高度z(m)表示为时间t(s)的函数;(2)点P第一次达到最高点大约需要多长时间？P0（A）点P在A点时开始计时；（B）点P在B点时开始计时；（C）点P在C点时开始计时；（D）点P在D点时开始计时。P 解：不妨设水轮沿逆时针方向旋转，如图建立平面直角坐标系。设是以Ox为始边，OP0为终边的角。由OP在ts内所转过的角为可知，以Ox为始边，OP为终边的角为，故P点的纵坐标为，则 （A）点P在A点时开始计时，则所求函数关系式为令，得，则，故，所以，当k=0时，t=。故点P第一次到达最高点需要s （B）点P在B点时开始计时，令，得，则，故，所以，当k=0时，t=0。故点P第一次到达最高点需要0s则所求函数关系式为 （C）点P在C点时开始计时，令，得，则，故，所以，当k=0时，t=。故点P第一次到达最高点需要s则所求函数关系式为 （D）点P在D点时开始计时，令，得，则，故，所以，当k=0时，t=。故点P第一次到达最高点需要s则所求函数关系式为 （A）点P在A点时开始计时；（B）点P在B点时开始计时；（C）点P在C点时开始计时；（D）点P在D点时开始计时。 变题：将圆心O上移2米，其余不变，试求解。 圣米切尔山涨潮落潮 潮汐对轮船进出港口产生什么影响？某港口在某季节每天的时间与水深关系表：时刻0：003：006：00水深/米5.07.55.0时刻9：0012：0015：00水深/米2.55.07.5时刻18：0021：0024：00水深/米5.02.55.0例3： A=2.5,h=5,T=12;由，得所以，这个港口的水深与时间的关系可以近似描述为：解：以时间为横坐标，水深为纵坐标，在直角坐标系中画出散点图，根据图象，可以考虑用函数来刻画水深与时间之间的对应关系.从数据和图象可以得出：由x=0时y=5，得；故即，由图可知；所以 由上述关系式易得港口在整点时水深的近似值：时刻0：001：002：003：004：005：00水深5.0006.2507.1657.57.1656.250时刻6：007：008：009：0010：0011：00水深5.0003.7542.8352.5002.8353.754时刻12：0013：0014：0015：0016：0017：00水深5.0006.2507.1657.57.1656.250时刻18：0019：0020：0021：0022：0023：00水深5.0003.7542.8352.5002.8353.754 小结： '