新人教版九年级上册24.1.4_圆周角课件PPT(精).ppt 24页

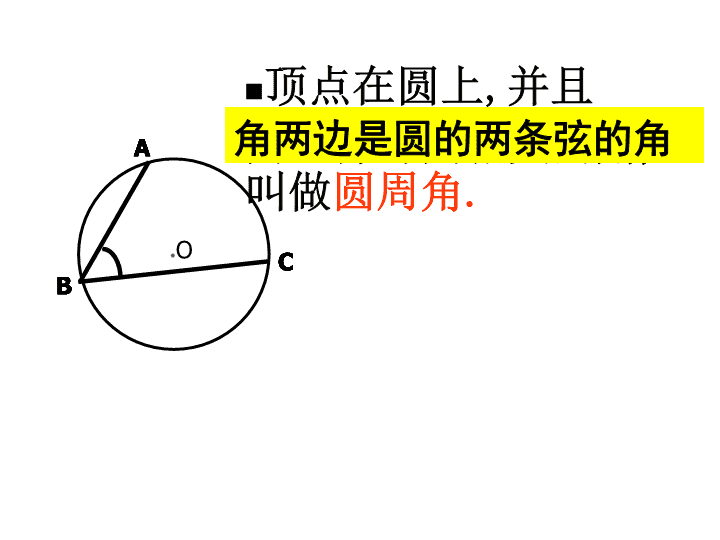
'24.1.4圆周角 一.复习引入:1.圆心角的定义?.OBC在同圆（或等圆）中，如果圆心角、弧、弦、弦心距有一组量相等，那么它们所对应的其余三组量都分别相等。答:顶点在圆心的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦、弦心距四组量之间关系的一个结论，这个结论是什么？ 顶点在圆上,并且两边都与圆相交的角,叫做圆周角.●OBACBACBACBACBACBAC角两边是圆的两条弦的角 辩一辩图中的∠CDE是圆周角吗?CDECDECDECDE 类比圆心角探知圆周角在同圆或等圆中,同弧或等弧所对的圆心角相等.在同圆或等圆中,同弧或等弧所对的圆周角有什么关系？为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.你会画同弧所对的圆周角和圆心角吗? 如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.●OABC●OABC●OABC 圆周角和圆心角的关系教师提示:注意圆心与圆周角的位置关系. 圆周角和圆心角的关系1.首先考虑一种特殊情况：当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角，∴∠AOC=∠B+∠A.∵OA=OB，●OABC∴∠A=∠B.∴∠AOC=2∠B.即∠ABC=∠AOC.同弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型. 如果圆心不在圆周角的一边上,结果会怎样?2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为1的情况?过点B作直径BD.由1可得:●O∴∠ABC=∠AOC.同弧所对的圆周角等于它所对的圆心角的一半.ABCD∠ABD=∠AOD,∠CBD=∠COD,圆周角和圆心角的关系●OABC 圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为1的情况?过点B作直径BD.由1可得:●O∴∠ABC=∠AOC.同弧所对的圆周角等于它所对的圆心角的一半.D∠ABD=∠AOD,∠CBD=∠COD,ABC●OABC 综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:同弧所对的圆周角等于它所对的圆心角的一半.●OABC●OABC●OABC即∠ABC=∠AOC. 如图所示，∠ADB、∠ACB、∠AOB分别是什么角？它们有何共同点？∠ADB与∠ACB有什么关系？同弧所对的圆周角相等.(等弧)思考:相等的圆周角所对的弧相等吗?在同圆或等圆中都等于这条弧所对的圆心角的一半.圆周角定理: 1.如图,在⊙O中,∠BOC=50°,求∠A的大小.●OBAC解:∠A=∠BOC=25°.ABOC如图,AB是直径,则∠ACB=＿＿＿＿90o半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径。 2.试找出下图中所有相等的圆周角。ABCD12345678∠2=∠7∠1=∠4∠3=∠6∠5=∠8 3：已知⊙O中弦AB的长等于半径，求弦AB所对的圆心角和圆周角的度数。OAB圆心角为60度圆周角为30度或150度。 4.如图，∠A是圆O的圆周角，∠A=40°，求∠OBC的度数。 例:如图，AB是⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D.求BC,AD,BD的长.106 练习:如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.ABOCD40° 练习：1、圆周角的两个特征：（1），（2）。2、在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的。3、如图，AB是⊙O的直径，∠AOD是圆心角，∠BCD是圆周角，若∠BCD=25°，则∠AOD=。顶点在圆上两边都与圆相交一半130° 4、如图，AB是⊙O的直径=，∠A=30°，则∠BOD=。5、如图，OA、OB、OC都是⊙O的半径，∠AOB=2∠BOC，∠ACB与∠BAC的大小有什么关系？为什么？60° 6、如图，A、B、C、D是⊙O上的四个点，且∠BCD=100°，求∠BOD（所对的圆心角）和∠BAD的大小。 这节课你有什么收获和体会，和大家一起分享一下吧！ 小结：1、圆周角的定义；2、圆周角定理及证明；3、圆周角定理的运用。作业：必做P88N3、5;P90N13,14 圆周角当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角有何特点?它们的大小有什么关系?.●OBACBACBACBACBACBACBACDEDE顶点在圆上,并且两边都与圆相交的角,叫做圆周角.'