最新图形折叠问题课件PPT.ppt 47页

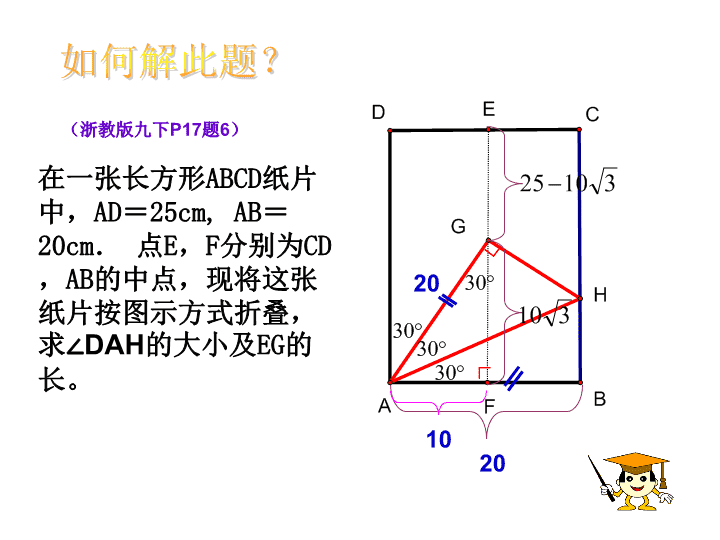
'图形折叠问题 在一张长方形ABCD纸片中，AD＝25cm,AB＝20cm．点E，F分别为CD，AB的中点，现将这张纸片按图示方式折叠，求∠DAH的大小及EG的长。（浙教版九下P17题6）如何解此题？201020 图形折叠问题既考查学生的动手能力，又考查了想象能力，往往与全等、相似、面积、对称性质联系在一起．涉及到画图、测量、猜想证明、归纳等问题，它与代数、几何均有联系．此类题目对于考查学生注重知识形成的过程，领会研究问题的方法有一定的作用，也符合新课改的教育理论。 例2、有一个数学活动，其具体操作过程是：第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）．请解答以下问题：（1）如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论．图1图2p（1）△BMP是等边三角形．证明：连结AN,∵EF垂直平分AB∴AN＝BN.由折叠知:AB＝BN∴AN＝AB＝BN∴△ABN为等边三角形∴∠ABN＝60°∴∠PBN＝30°又∵∠ABM＝∠NBM＝30°，∠BNM＝∠A＝90°∴∠BPN＝60°,∠MBP＝∠MBN＋∠PBN＝60°∴∠BMP＝60°∴∠MBP＝∠BMP＝∠BPM＝60°∴△BMP为等边三角形． 例2、（2）在图2中，若AB＝a，BC＝b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP？图1图2pab （3）设矩形ABCD的边AB＝2，BC＝4，并建立如图3所示的直角坐标系.设直线BM/为y=kx，当∠M/BC＝60°时，求k的值.此时，将△ABM′沿BM′折叠，点A是否落在EF上（E、F分别为AB、CD中点）？为什么？例2、第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2）．图1图2图3 A/H2 例3.（2007年济宁市）如图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE.过B点折纸片使D点叠在直线AD上，得折痕PQ.(1)求证：△PBE∽△QAB；(2)你认为△PBE和△BAE相似吗？如果相似给出证明，如不相似请说明理由；(3)如果沿直线EB折叠纸片，点A是否能叠在直线EC上？为什么？ 例4.如图，长方形ABCD沿AE折叠，使D落在边BC上的F点处，如果∠BAF=60°，则∠DAE=ABCDFE根据折叠的规律：可证△ADE≌△AFE,从而∠DAE=∠FAE=(90°--60°)÷2=15°15°60°15°15° ABCDFE透过现象看本质:折叠轴对称实质轴对称性质：ADEF1.图形的全等性：重合部分是全等图形，对应边角相等.2.点的对称性：对称点连线被对称轴（折痕）垂直平分.由折叠可得：1.△AFE≌△ADE2.AE是DF的中垂线 例5.如图，折叠长方形的一边AD，点D落在BC边的点F处，已知AB=8cm,BC=10cm,求EC的长分析：设EC=x,则EF=DE=8-x.在Rt△ABF中，AF=AD=10，AB=8，所以BF=6，FC=4Rt△POE∽Rt△BPA解得EC=3(cm)ABCDFE81010643 例6.（08浙江宁波）如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸的短边长为a.（1）如图2，把这张标准纸对开得到的“16开”张纸按如下步骤折叠：第一步将矩形的短边AB与长边AD对齐折叠，点B落在AD上的点B’处，铺平后得折痕AE；第二步将长边AD与折痕AE对齐折叠，点D正好与点E重合，铺平后得折痕AF．则AD:AB的值是，AD,AB的长分别是，．ABCDFEB’4开2开8开16开图1图2a（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个比值；若不相等，请分别计算它们的比值．相等，比值为 例7.（2007年台州市）如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边BC折叠，使点B落在边OA的点D处．已知折痕        ，且            (1)判断△OCD与△ADE是否相似？请说明理由；(2)求直线CE与x轴交点P的坐标；P6X8X3X4X10X5X5X 关键是找出对称点，并画出来。依线翻折 例8.08湖州已知：在矩形AOBC中，OB=4,OA=3．分别以OB,OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是边BC上的一个动点（不与B,C重合），过F点的反比例函数的图象与AC边交于点E．请探索：是否存在这样的点F，使得将△CEF沿EF对折后，C点恰好落在OB上？若存在，求出点F的坐标；若不存在，请说明理由．（,3）(4,)3 例9.在平面直角坐标系中，正方形ABCO的边长为6，两边OA、OC分别落在坐标轴上，点E在射线BC上，且BE=2CE，将△ABE沿直线AE翻转，点B落在点B1处。（1）请在图中作出点B1及翻转后图形.0CBAyx0CBAyEB1（2）对于图1，若E在BC上，求点B1的坐标。两种情况F利用相似，列出方程求解E0CBAyB1x图1图264a6-a46 例10.（07湖北荆门）如图1，在平面直角坐标系中，有一张矩形纸片OABC，已知O(0，0)，A(4，0)，C(0，3)，点P是OA边上的动点(与点O、A不重合)．现将△PAB沿PB翻折，得到△PDB；再在OC边上选取适当的点E，将△POE沿PE翻折，得到△PFE，并使直线PD、PF重合．(1)设P(x，0)，E(0，y)，求y关于x的函数关系式，并求y的最大值；图1解：(1)由已知PB平分∠APD，PE平分∠OPF，且PD、PF重合，则∠BPE=90°．∴∠OPE＋∠APB=90°．又∠APB＋∠ABP=90°，∴∠OPE=∠PBA．∴Rt△POE∽Rt△BPA．∴y=(0＜x＜4)∴即xy4-x3 (2)如图2，若翻折后点D落在BC边上，求过点P、B、E的抛物线的函数关系式；图2(2)由已知，△PAB、△POE均为等腰直角三角形，可得P(1，0)，E(0，1)，B(4，3)．故该抛物线上存在两点Q(4，3)、(5，6)满足条件．则∴y= 例11.直线分别与x轴、y轴交于B、A两点.把△AOB以直线AB为轴翻折，点O落在平面上的点C处，再把△BOC以直线BC为轴翻折得△BCE，求点E的坐标. 由（1）知OA＝1，OB＝，∴∠OBA＝30°.∵△ABC和△ABO关于AB成轴对称，　∴BC＝BO＝，∠CBA=∠OBA＝30°.∴∠CBO＝60°.过点C作CM⊥x轴于M，如图，则在Rt△BCM中，. 图形翻折实际上是轴对称变换，变换前后的对应线段相等、对应角相等。常常与角平分线、中线、线段中垂线、等腰三角形的高相联系。解决翻折的动态几何问题关键是结合直角三角形或全等三角形或相似三角形的有关知识，全面寻找图形运动过程中的不变量。 ABCD例12.（08山东东营）：将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去上方的小三角形．将纸片展开，得到的图形是（）C 例13．将正方形纸片两次对折，并剪出一个菱形小洞后展开铺平，得到的图形是（）C 例14.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（　　）EDCBADCBAFEDCBAA．4B．6C．8D．10６６４２２C４４ 图形折叠问题中题型的变化比较多，但是经过研究之后不难发现其中的规律，从今天我们对矩形折叠情况的讨论中可以得到以下几点经验：1．图形的翻折部分在折叠前和折叠后的形状、大小不变，是全等形；2．图形的翻折部分在折叠前和折叠后的位置关于折痕成轴对称；3．解决折叠问题时，要抓住图形之间最本质的位置关系，从而进一步发现其中的数量关系；4．充分挖掘图形的几何性质，将其中的基本的数量关系，用方程的形式表达出来，并迅速求解，这是解题时常用的方法之一。 谢谢大家，欢迎批评指正！ 五色入五脏，五味入五脏30 青绿色---酸味的食物对肝有益，比如：黄瓜红色------苦味的食物对心有益，比如：红枣、榴莲黄色------甜味的食物对脾有益，比如：大豆、地瓜白色------辣味的食物对肺有益，比如：杏仁、山葯、洋葱黑色------咸味的食物对肾有益，比如：葡萄、茄子31 配制三色或三味以上的混合果汁葡萄山葯汁（2：1）；苦瓜蜂蜜汁。32 人体饮食健康的最大敌人食盐和味精。因此一定要控制食盐和味精的摄入量。食盐每天的摄入量最高是6克，味精不放或少放。33 酸------肝，苦-----心，甜-----脾，辣------肺、咸------肾，34 眼睛如果，你的眼睛，经常发花、眼角干涩、看不清东西。这就说明，肝脏功能开始衰落，是肝病的先兆。这时，你可以按一按，肝脏的四周，如果发现有发胀的感觉。你要及时就医，还要注意生活上用眼卫生。有时，用眼不当，也会影响到肝脏健康。35 耳朵如果，你的耳朵，老是嗡嗡作响，声音也听不太清楚。这就说明，肾功能正在逐步衰弱，是肾衰的重要信号。这时，你如果还出现阵阵的脚痛与尿频等症状，更是证明肾衰的开始。特别是，那么一些工作过于劳累的人，尤其要注意做到劳逸结合，少饮酒，少吃姜、辣椒等刺激性强的食物。36 鼻子如果，你感觉到鼻子的嗅觉不灵敏，还出现经常的咳嗽，甚至有时呼吸困难。这说明，肺脏功能正在逐步衰弱，是肺衰的重要信号。这时，你首先就要注意饮食，立即戒烟，或者控制吸烟量，注意不要和经常吸烟的人在一起！平时，多注意吃新鲜瓜果和蔬菜，注意加强体育锻炼，防止肺部并发症的发生。37 嘴唇如果，你嘴唇感觉到麻木，身体日渐消瘦。这说明，胰脏功能正在逐步衰弱，是胰脏失调的先兆。原因是你的饮食失调、饥饱不当所致。由于胰脏不好，就会殃及胃。当你的胃，受到损害时，你的嘴唇，就会明显地变得干燥、麻木。这时，你一定要调整饮食，还要注意到不要吃生冷、油腻的食品。38 舌头如果，你舌头味觉感觉迟钝，尝不出味道，而且还伴随心悸、梦多、失眠等症状。这说明，你的心脏功能受到损害，心脏衰弱的先兆。原因可能是你操劳过度所致。特别是，当你觉得口中干涩，舌苔厚重，尝不出食物的滋味一系列症状时，这时特别要警惕心脏发生病变39 五色可以协调人的容颜美青色应肝,酸味入肝,所以面色发青的人,不宜多服青色及味酸的食物赤色应心,苦味入心,故而要想面色红润,可补以红色,味苦的食物,如西红市,橘子.红苹果黄色应脾,甘味入脾,所以容颜缺少明黄色的,可辅以黄色,味甘的食物,如胡萝卜,蛋黄一类.白色应肺,辛味入肺,故想肌肤美白,可常食白色,辛味的食物,如牛奶,豆浆一类黑色应肾,咸味入肾,所以面黑者应少吃黑色及咸味食40 五味过量。五味适量，对五脏有补益作用，但是如果五味会打乱人体平衡，损伤脏器，招致疾病。《彭祖摄生养性论》中说：“五味不得偏耽，酸多伤脾，苦多伤肺，辛多伤肝，甘多伤肾，咸多伤心。”《内经》中也说：“多食咸，则脉凝泣而变色；多食苦，则皮槁而毛拔；多食辛，则筋急而爪枯；多食酸，则肉胝皱而唇揭；多食甘，则骨痛而发落，此五味之所伤也。”41 酸多伤脾酸味可以补肝，过多的酸味食物会引起肝气偏胜，就会克伐脾胃(木克土)。由于脾主肌肉，其华在唇，酸味的东西吃得过多，就会使肌肉角质变厚，即“肉胝皱”，嘴唇也会失去光泽，并往外翻，即“唇揭”。同时还常出现饭量减少，饭后胃胀，大便稀，言语低微等脾气虚的症状。42 甘多伤肾甘味可以补脾，过多的甘味食物会引起脾气偏胜，就会克伐肾脏(土克水)。由于肾主骨藏精，其华在发，因此甜味的东西吃多了就会使头发失去光泽、脱落。同时还常出现腰膝酸软、耳鸣耳聋等肾精虚的症状。43 咸多伤心咸味可以补肾，过多的咸味食物会引起肾气偏胜，就会克伐心脏(水克火)。由于心主血，咸味的东西吃多了，就会影响气血的生发和运行，使血脉凝滞，脸色变黑。同时还常出现心悸、气短、胸痛等症状。44 苦多伤肺苦味可以补心，过多的苦味食物会引起心气偏胜，就会克伐肺脏(火克金)。由于肺主皮毛，苦味的东西吃多了皮肤就会枯槁，毛发就会脱落，即“皮槁而毛拔”。同时还常出现咳嗽、咳痰等肺气虚的症状。45 辛多伤肝辛味可以补肺，过多的辛味食物会引起肺气偏胜，就会克伐肝脏(金克木)。由于肝藏血，主筋，辛味的东西吃多了，会导致肝血不足，筋脉失血，爪甲失荣。同时还常出现头晕目眩、面色无华、视物模糊等肝血虚的症状。46 五官、五味、五脏、五色、五行对应五指口--甜----脾---黄---土---拇指目--酸----肝---青---木---食指舌--苦----心---赤---火---中指耳--咸----肾---黑---水---无名指鼻--辛----肺---白---金----小指47'