最新湘教版数学八年级下册(新)-课件：2.3《中心对称与中心对称图形》(共31张PPT)课件PPT.ppt 51页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。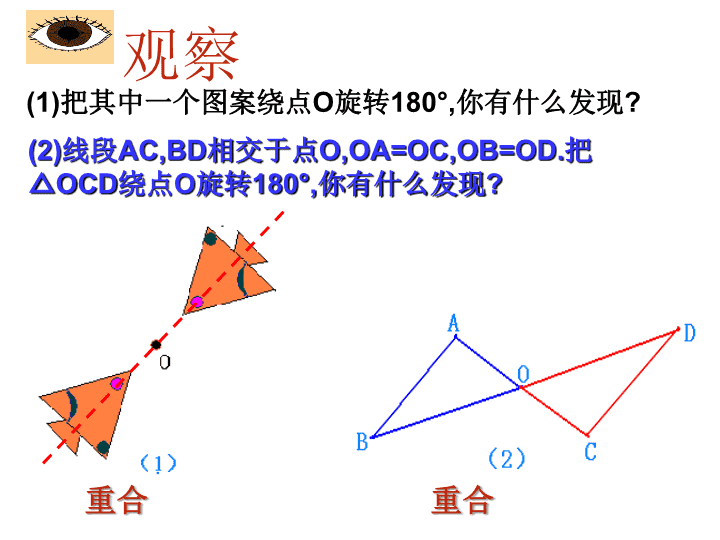　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅湘教版数学八年级下册(新)-课件：2.3《中心对称与中心对称图形》(共31张PPT) (1)把其中一个图案绕点O旋转180°,你有什么发现?重合重合观察(2)线段AC,BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你有什么发现? 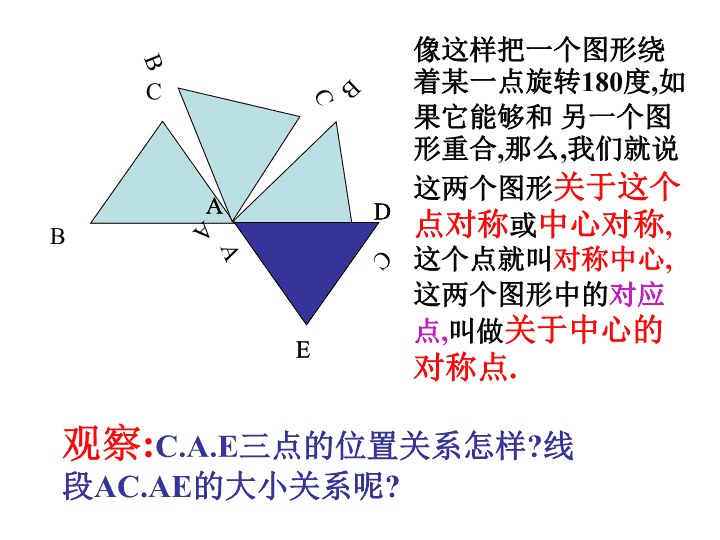ACBACBACBADE像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.观察:C.A.E三点的位置关系怎样?线段AC.AE的大小关系呢?ADE 想一想中心对称与轴对称有什么区别?又有什么联系?轴对称中心对称有一条对称轴---直线有一个对称中心---点图形沿对称轴对折(翻折1800)后重合图形绕对称中心旋转1800后重合对称点的连线被对称轴垂直平分对称点连线经过对称中心,且被对称中心平分 AA′B′BO2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法灵活运用，体会内涵以点O为对称中心,作出点A的对称点A′;以点O为对称中心,作出线段AB的对称线段点A′B′点A′即为所求的点 例1(2)如图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。 例1（3）已知四边形ABCD和点O，画四边形A′B′C′D′，使它与已知四边形关于这一点对称。ABA’C’B’D’DOC四边形A１B１C１D１即为所求的图形。 画一个与已知四边形ABCD中心对称图形。（1）以顶点A为对称中心；（2）以BC边的中点为对称中心。提高练习DABCEFGMDABCO．N 如图，已知△ABC与△A’B’C’中心对称，求出它们的对称中心O。ABCA’B’C’深入理解 解法一：根据观察，B、B’应是对应点，连结BB’，用刻度尺找出BB’的中点O，则点O即为所求（如图）ABCA’B’C’O O解法二：根据观察，B、B’及C、C’应是两组对应点，连结BB’、CC’，BB’、CC’相交于点O，则点O即为所求（如图）。ABCA’B’C’ 深入理解你用什么方法识别两个图形是否关于某点中心对称？A"CC"ABB" 方法1：将其中一个图形绕某一点旋转180度，如果能够与另一个完全重合，那么它们关于这一点中心对称。方法2：如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称. （1）这些图形有什么共同的特征？旋转一定的角度可以和自身重合（2）这些图形的不同点在哪？分别绕旋转中心旋转多少度可以和原图形重合？第一个图形的旋转角度为120°或240°，第二个图形的旋转角度为72°或144°或216°或288°。后三个图形的旋转角度都为180°，第二，三个是轴对称图形。后三个图形都是旋转1800后能与自身重合复习与思考 O如果一个图形绕一个点旋转180°后，能和原来的图形互相重合，那么这个图形叫做中心对称图形；这个点叫做它的对称中心；互相重合的点叫做对称点.观察与发现BACD图中_________是中心对称图形对称中心是______点O点A的对称点是______点D的对称点是______ABCD点C点B （1）（2）（3）（4）旋转图形（1）旋转图形（2）旋转图形（3）旋转图形（4）下列图形是中心对称图形吗？点击跳转问题与讨论 返回旋转 返回旋转 返回旋转 旋转 都是中心对称图形 观察图形，并回答下面的问题：（１）哪些只是轴对称图形？（２）哪些只是中心对称图形？（３）哪些既是轴对称图形，又是中心对称图形？（１）（３）（２）（４）（５）（６）（3）（4）（6）（1）（2）（5）巩固提高 2.在①线段、②角、③等腰三角形、④等腰梯形、⑤平行四边形、⑥矩形、⑦菱形、⑧正方形和⑨圆中，是轴对称图形的有______________,是中心对称图形的有____________,既是轴对称图形又是中心对称图形的有____________.①⑤⑥⑦⑧⑨①②③④⑥⑦⑧⑨①⑥⑦⑧⑨B巩固提高 在26个英文大写正体字母中，哪些字母是中心对称图形？哪些字母是轴对称图形？ABCDEFGHIJKLMNOPQRSTUVWXYZ 工农业生产旋转的物体必须具有稳定性，而中心对称的设计恰恰满足了旋转物体的这一需求。因而在工农业生产制作转动工具时，都不可避免地考虑应用中心对称的设计，小的如日常生活中单车、闹钟内的齿轮，电风扇的扇叶；大的如推动飞机、轮船的轮桨，风力发电用的风车等等。另外，在日常使用的一些生活工艺品（如：地毯、挂毯），也不难发现中心对称的影子！ 名称中心对称中心对称图形定义把一个图形绕着某一个点旋转180,如果他能够与另一个图形重合，那么就说这两个图形关于这点对称，这个点叫做对称中心,两个图形关于点对称也称中心对称，这两个图形中的对应点叫做关于中心的对称点如果一个图形绕着一个点旋转180后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心性质①两个图形可完全重合；②对应点连线都经过对称中心，并且被对称中心平分①是一个特殊的图形②对应点连线都经过对称中心，并且被对称中心平分区别①两个图形的关系②对称点在两个图形上①具有某种性质的一个图形②对称点在一个图形上联系若把中心对称图形的两部分分别看作两个图形，则它们成中心对称，若把中心对称的两个图形看作一个整体，则成为中心对称图形。小结中心对称与中心对称图形有什么区别与联系？ ☆知识巩固2、中心对称有何性质？1什么叫中心对称和中心对称图形？（2）关于中心对称图形的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。（1）关于中心对称图形的两个图形是全等形。3、在下列图形中，是中心对称图形的是（）C 4、下列美丽的图案，既是轴对称图形又是中心对称图形的个数是()A.1个B.2个C.3个D.4个5、画出△ABC关于点O的中心对称图形．C分析：中心对称就是旋转180°，关于点O成中心对称就是绕O旋转180°，因此，我们连AO、BO、CO并延长，取与它们相等的线段即可得到． 第二章　信号分析与信息论基础2.1　确知信号分析2.2　随机信号分析2.3　信息及信息的度量2.4　信道统计特性 本章教学内容及要求信号通过系统的过程。确定信号的时域和频域分析。傅立叶变换关系式，傅立叶变换的主要运算特性，常用信号的付立叶变换。卷积定义式，时域卷积定理，频域卷积定理。信号的能量和能量谱密度；信号的功率和功率谱密度。信号的表达方法，信号通过线性系统传输后的变化及表达。信息及信息量、信道模型、随参信道传输媒质的特点、信道容量计算。 2.1　确知信号分析信号是通过电的某一物理量（如电压或电流）表示出的与时间t之间的函数关系。确知信号：能用函数表达式准确表示出来的信号。它与时间的关系是确知的。随机信号：与上述相反。通信中传输的信号及噪声都是随机信号。2.1.1　周期信号与非周期信号周期信号：满足条件s(t)=s(t+T0)-∞＜t＜∞，T0＞0非周期信号：不满足上述条件。功率信号：信号在（0，T）内的平均功率S(式2-2)值为一定值。能量信号：当T→∞时，式(2-3)是绝对可积的。 2.1.2　信号的傅里叶变换傅里叶变换：式(2-7)傅里叶反变换：式(2-6)式（2-8）是傅里叶变换的指数形式，傅里叶变换是一个连续函数，称为频谱密度函数，简称频谱函数。典型的连续时间信号：1.Sa(t)信号（抽样信号）：Sa(t)=sin(t)/t波形特点：偶函数；零值点（±nπ）；(0~∞)的积分为π/22.单位阶跃信号：U(t)=0(t<0);U(t)=1(t>0);3.单位冲激信号：∫例：（1）阶跃信号构成矩形脉冲信号：　g(t)=u(t)-u(t-t0)（2）阶跃信号构成符号函数：Sgn(t)=2u(t)-1 常用信号的傅里叶变换：矩形函数（图2-1）的傅里叶变换见式（2-9），其频谱函数见图（2-2）。冲激函数的傅里叶变换。余弦函数的傅里叶变换。傅里叶变换的性质：时移特性：频移特性：时域卷积与频域卷积时域卷积：Γ[f1(t)*f2(t)]=F1(ω)F2(ω)频域卷积：Γ[f1(t)f2(t)]=(1/2π)[F1(ω)*F2(ω)] 例：已知　Γ[f(t)]=F(ω)求　　Γ[f(t)COSω0t]=?解：Γ[COSω0t]=π[δ(ω-ω0)+δ(ω+ω0)]冲激强度为π，根据卷积定理：Γ[f(t)COSω0t]=（1/2π)F(ω)*{π[δ(ω-ω0)+δ(ω+ω0)]}=(1/2)[F(ω-ω0)+F(ω+ω0)]2.1.3　信号通过线性系统线性系统：输出信号与输入信号满足线性关系（允许有延迟）。f0(t)=Kfi(t-td)（2-13）该系统传递函数：H(ω)=式（2-14）线性不失真系统的幅频特性|H(ω)|是与ω无关的常数，相频特性则是ω的线性函数。 2.2　随机信号分析2.2.1高斯平稳随机过程1、随机过程的一般概念通信过程中的随机信号和噪声均可归纳为依赖于时间参数t的随机过程。这种过程的基本特征是，它是时间t的函数，但在任一时刻观察到的值却是不确定的，是一个随机变量。2、随机过程的定义定义：随机过程是依赖于时间参量t变化的随机变量的总体或集合；也可以叫做样本函数的总体或集合。习惯用ξ(t)表示。3、随机过程的统计特性的描述设ξ(t)表示一个随机过程，则在任意一个时刻t1上，ξ(t1)是一个随机变量。显然，这个随机变量的统计特性，可以用概率分布函数或概率密度函数去描述。 4、随机过程的数字特征随机过程的数字特性，比如，随机过程的数学期望、方差及相关函数等。1）数学期望随机过程ξ(t)的数学期望被定义为可把t1直接写成t。随机过程的数学期望被认为是时间t的函数。数学期望的物理意义：信号或噪声的直流功率。2）方差随机过程的方差定义为方差的物理意义：信号或噪声交流功率。 3）自相关函数5、平稳随机过程狭义平稳概念：所谓平稳随机过程，是指它的任何n维分布函数或概率密度函数与时间起点无关。也就是说，如果对于任意的n和τ，随机过程ξ(t)的n维概率密度函数满足：则称ξ(t)是平稳随机过程。6、广义平稳过程广义平稳概念：若一个随机过程的数学期望及方差与时间无关，而其相关函数仅与τ有关，则称这个随机过程为广义平稳随机过程。用途：a、用来判断广义平稳；b、用来求解随机过程的功率谱密度及平均功率。 通信系统中的信号及噪声，大多数可视为平稳的随机过程。因此，研究平稳随机过程有很大的实际意义。7、自相关函数我们已经知道，平稳随机过程的自相关函数和时间t无关，而只与时间间隔τ有关，即：R(τ)＝E{ξ(t)ξ(t+τ)}自相关函数的性质：1）R(0)为ξ(t)的均方值(平均功率)。自相关函数在τ=0处的数值等于该过程的平均功率(包括直流功率和交流功率)。2）对偶性R(τ)＝R(－τ)即自相关函数是τ的偶函数。 证明：3）当τ＝0时,自相关函数取最大值，即R(0)≥R(τ)4）5)8、功率谱密度：付氏变换沟通了确定信号时域和频域的关系，那么为什么随机过程在频率域中要讨论功率谱密度，而不讨论付氏变换呢？主要原因有二。1)、对于随机过程来说，它由许许多多个样本函数来构成,所以我们无法求其付氏变换，可以说,随机过程不存在付氏变换。 2)、随机过程属于功率信号而不属于能量信号，所以我们讨论功率谱密度。对于任意的功率信号f(t)的功率谱为：9、高斯分布概率密度函数由f(x)的表达式可画出图形9、高斯分布和高斯过程高斯分布这个概念在通信中是经常出现的。而在一般情况下，噪声都可以认为具有高斯分布的形式。由信息论的观点来说，如果是连续信源，当信号的功率一定时，信号幅度的概率密度函数服从高斯分布时，载 荷的信息量最大，即有效性最好；另一方面，如果是起伏噪声，当噪声功率Ｎ一定时，幅度呈现高斯分布的噪声对通信系统的影响也最为恶劣。因此，在系统设计中，常以高斯噪声为着眼点来考虑信噪比、带宽等问题。因此，高斯分布是通信系统的统计分析中最常见、最重要的一种分布。高斯过程定义：通俗地讲，在任意时刻t去观察随机过程，若其随机变量的概率分布都满足高斯分布,这个随机过程就是高斯过程。2.2.2窄带高斯噪声任何通信系统都有发送机和接收机，为了提高系统的可靠性，即输出信噪比，通常在接收机的输入端接有一个带通滤波器，信道内的噪声构成了一个随机过程，经过该带通滤波器之后，则变成了窄带随机过程。 窄带条件：中心频率为ω0，带宽为△f，当△ω<<ω0时，就可认为满足窄带条件。若随机过程的功率谱满足该条件则称为窄带随机过程。若带通滤波器的传输函数满足该条件则称为窄带滤波器。随机过程通过窄带滤波器传输之后变成窄带随机过程。（图2-7）（图2-8）窄带过程的数学表示1、用包络和相位的变化表示由窄带条件可知,窄带过程是功率谱限制在ω0附近的很窄范围内的一个随机过程,从示波器观察(或由理论上可以推知):这个过程中的一个样本函数(一个实现)的波形是一个频率为ω0且幅度和相位都做缓慢变化的余弦波。所以可以表示成： 2.3.1通信系统的统计模型（图2-12）信源：通信的起点。输出消息（包括文字、符号、声音、图像、数据等）。信源编码器：将消息变为信号（提高信号传输效率）。信道编码器：信号处理的设备（提高信号传输的的可靠性）。干扰源：即噪声源。2.3.2信息的定义从统计学的信息指的是消息中包含的不确定性。2.3.3信息的度量信息的度量，与信息发生的概率成反比。如果一个事件发生的概率是1，这是一个必然事件，那么它的信息量就是0。离散信源信息量I=loga(1/P(x))=-loga(P(x))(2-58)2.3　信息及信息的度量 P(x)为事件发生的概率，若a=2，信息量单位为比特（bit）;若a=e，信息量单位为奈特（nit）;若a=10，信息量单位为哈特莱。式（2-59）求信息量总和例2-1、例2-2、例2-3。2.3.4离散信源的平均信息量如离散信息信号序列发生的概率如下所示。符号xix1x2……xn符号发生概率P(xi)P(x1)P(x2)……P(xn)这样每个符号的平均信息量（也称为熵）为H（x） 可以证明，当每个符号等概率出现时，平均信息量最大。式（2-62）例2-4。2.3.5连续信源的平均信息量当连续信源出现的概率密度为f(x)时，连续信源的平均信息量为即为连续信源的熵，又称为相对熵。例2-5。 2.4.1离散信道的信道容量信道容量：信道在理想状态下（无差错传输或差错率等于零）的最大传信速率，通常用C表示。条件熵定义（2-67）（2-68）互信息量定义（2-69）（2-70）无损信道：H（x/y)=0,I(x,y)=H(x)=H(y)全损信道：H（x/y)=H(x)Rt=RB[H(x)-H(x/y)]=Ht(x)-Ht(x/y)(bit/s)(2-71)实际信息传输速率Rt的最大值记为C，即C=maxRt=max[Ht(x)-Ht(x/y)](2-72)例2-6、2-7。2.4　信道统计特性 2.4.2　连续信道的信道容量香农信道容量公式：C=Blog2(1+s/(n0B))(bit/s)(2-78)式中，B为信道带宽（Hz)，S为信号功率（W），n0为噪声单边功率谱密度（W/Hz)，N=n0B为噪声功率（W）。上式成立的条件是：信号为高斯分布（此时信息熵最大），噪声为高斯白噪声。香农信道容量公式告诉我们以下重要结论：①C随S/N增大而增大；②当n0→0时C→∞，即无干扰信道的信道容量为无穷大；③C随着B的增大而增大，但不能无限增大，即当B→∞时，C→1.44(S/n0)④C一定时，B与S/N可以互换； ⑤若信源信息速率Rb≤C，则理论上可以实现无差错传输。若Rb＞C，则不可能实现无差错传输。信道容积Vc的概念信号体积Vs≤信道容积Vc时才能实现通信'