高等数学课件PPT10 223页

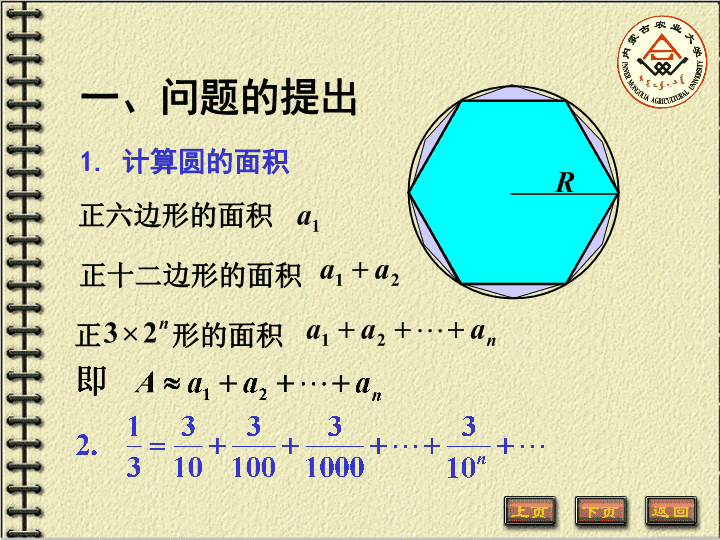
'第十章 一、问题的提出1.计算圆的面积正六边形的面积正十二边形的面积正形的面积 二、级数的概念1.级数的定义:(常数项)无穷级数一般项部分和数列级数的部分和 2.级数的收敛与发散: 余项无穷级数收敛性举例：Koch雪花.做法：先给定一个正三角形，然后在每条边上对称的产生边长为原边长的1/3的小正三角形．如此类推在每条凸边上都做类似的操作，我们就得到了面积有限而周长无限的图形——“Koch雪花”． 观察雪花分形过程第一次分叉：依次类推播放 周长为面积为第次分叉： 于是有结论：雪花的周长是无界的，而面积有界．雪花的面积存在极限（收敛）． 解 收敛发散发散发散综上 解 三、基本性质结论:级数的每一项同乘一个不为零的常数,敛散性不变.结论:收敛级数可以逐项相加与逐项相减. 证明类似地可以证明在级数前面加上有限项不影响级数的敛散性. 证明 注意收敛级数去括弧后所成的级数不一定收敛.收敛发散 四、收敛的必要条件证明级数收敛的必要条件: 注意1.如果级数的一般项不趋于零,则级数发散;发散2.必要条件不充分. 讨论 8项4项2项2项项由性质4推论,调和级数发散. 五、小结常数项级数的基本概念基本审敛法 思考题 思考题解答能．由柯西审敛原理即知． 练习题 练习题答案 观察雪花分形过程第一次分叉：依次类推 观察雪花分形过程第一次分叉：依次类推 观察雪花分形过程第一次分叉：依次类推 观察雪花分形过程第一次分叉：依次类推 观察雪花分形过程第一次分叉：依次类推 观察雪花分形过程第一次分叉：依次类推 一、正项级数及其审敛法1.定义:这种级数称为正项级数.2.正项级数收敛的充要条件:定理部分和数列为单调增加数列. 证明即部分和数列有界3.比较审敛法 不是有界数列定理证毕.比较审敛法的不便:须有参考级数. 解由图可知 重要参考级数:几何级数,P-级数,调和级数. 证明 4.比较审敛法的极限形式:设å¥=1nnu与å¥=1nnv都是正项级数,如果则(1)当时,二级数有相同的敛散性;(2)当时，若收敛,则收敛;(3)当时,若å¥=1nnv发散,则å¥=1nnu发散; 证明由比较审敛法的推论,得证. 解原级数发散.故原级数收敛. 证明 收敛发散 比值审敛法的优点:不必找参考级数.两点注意: 解 比值审敛法失效,改用比较审敛法 级数收敛. 二、交错级数及其审敛法定义:正、负项相间的级数称为交错级数. 证明 满足收敛的两个条件,定理证毕. 解原级数收敛. 三、绝对收敛与条件收敛定义:正项和负项任意出现的级数称为任意项级数.证明 上定理的作用：任意项级数正项级数 解故由定理知原级数绝对收敛. 四、小结正项级数任意项级数审敛法1.2.4.充要条件5.比较法6.比值法7.根值法4.绝对收敛5.交错级数(莱布尼茨定理)3.按基本性质; 思考题 思考题解答由比较审敛法知收敛.反之不成立.例如：收敛,发散. 练习题 练习题答案 一、函数项级数的一般概念1.定义: 2.收敛点与收敛域: 函数项级数的部分和余项(x在收敛域上)注意函数项级数在某点x的收敛问题,实质上是数项级数的收敛问题.3.和函数:(定义域是?) 解由达朗贝尔判别法原级数绝对收敛. 原级数发散.收敛;发散; 二、幂级数及其收敛性1.定义:2.收敛性: 证明 由(1)结论几何说明收敛区域发散区域发散区域 推论 定义:正数R称为幂级数的收敛半径.幂级数的收敛域称为幂级数的收敛区间.规定问题如何求幂级数的收敛半径? 证明 由比值审敛法, 定理证毕. 例2求下列幂级数的收敛区间:解该级数收敛该级数发散 发散收敛故收敛区间为(0,1]. 解缺少偶次幂的项级数收敛, 级数发散,级数发散,级数发散,原级数的收敛区间为 三、幂级数的运算1.代数运算性质:(1)加减法(其中 (2)乘法(其中柯西乘积 (3)除法(相除后的收敛区间比原来两级数的收敛区间小得多)2.和函数的分析运算性质: (收敛半径不变) (收敛半径不变) 解两边积分得 解收敛区间(-1,1), 常用已知和函数的幂级数 四、小结2.幂级数的收敛性:收敛半径R3.幂级数的运算:分析运算性质1.函数项级数的概念: 思考题幂级数逐项求导后，收敛半径不变，那么它的收敛域是否也不变？ 思考题解答不一定.例它们的收敛半径都是1,但它们的收敛域各是 练习题 练习题答案 一、泰勒级数上节例题存在幂级数在其收敛域内以f(x)为和函数问题:1.如果能展开,是什么?2.展开式是否唯一?3.在什么条件下才能展开成幂级数? 证明 泰勒系数是唯一的,逐项求导任意次,得泰勒系数 问题定义泰勒级数在收敛区间是否收敛于f(x)?不一定. 可见在x=0点任意可导, 证明必要性 充分性 证明 二、函数展开成幂级数1.直接法(泰勒级数法)步骤: 例1解由于M的任意性,即得 例2解 例3解 两边积分得 即牛顿二项式展开式注意: 双阶乘 2.间接法根据唯一性,利用常见展开式,通过变量代换,四则运算,恒等变形,逐项求导,逐项积分等方法,求展开式.例如 例4解 三、小结1.如何求函数的泰勒级数;2.泰勒级数收敛于函数的条件;3.函数展开成泰勒级数的方法. 思考题什么叫幂级数的间接展开法？ 思考题解答从已知的展开式出发,通过变量代换、四则运算或逐项求导、逐项积分等办法,求出给定函数展开式的方法称之. 练习题 练习题答案 一、近似计算两类问题:1.给定项数,求近似值并估计精度;2.给出精度,确定项数.关健:通过估计余项,确定精度或项数. 常用方法:1.若余项是交错级数,则可用余和的首项来解决;2.若不是交错级数,则放大余和中的各项,使之成为等比级数或其它易求和的级数,从而求出其和.例1解 余和: 例2解其误差不超过. 二、计算定积分解法逐项积分展开成幂级数定积分的近似值被积函数 第四项取前三项作为积分的近似值,得例3解收敛的交错级数 三、求数项级数的和1.利用级数和的定义求和:(1)直接法;(2)拆项法;(3)递推法.例4解 2.阿贝尔法(构造幂级数法):(逐项积分、逐项求导)例4解 例5解 四、欧拉公式复数项级数: 复数项级数绝对收敛的概念三个基本展开式 揭示了三角函数和复变数指数函数之间的一种关系.欧拉公式 五、小结１、近似计算,求不可积类函数的定积分，２、微分方程的幂级数的解法．(第十二节介绍)求数项级数的和，欧拉公式的证明； 思考题利用幂级数展开式,求极限 思考题解答将上两式代入 原式= 练习题 练习题答案 一、问题的提出问题: 解得和函数：因为该级数每一项都在[0,1]是连续的，例1考察函数项级数和函数的连续性． 结论问题 二、函数项级数的一致收敛性定义 xyo几何解释: 例2解余项的绝对值 例3研究例1中的级数在区间(0,1]内的一致收敛性.解对于任意一个自然数 因此级数在(0,1)内不一致连续．说明:从下图可以看出:但虽然函数序列在(0,1)内处处在(0,1)内各点处收收敛于敛于零的“快慢”程度是不一致的． (1,1)1小结一致收敛性与所讨论的区间有关． 定理　（魏尔斯特拉斯(Weierstrass)判别法）一致收敛性简便的判别法： 证 例4证明级数 证 三、一致收敛级数的基本性质定理1证 (1)(2)同样有 (3)由(1)、(2)、(3)可见, 定理2(4) 证 根据极限定义，有即 定理3(5) 注意:级数一致收敛并不能保证可以逐项求导.例如，级数逐项求导后得级数所以原级数不可以逐项求导． 定理4幂级数的一致收敛性 定理5 证于是 四、小结1、函数项级数一致收敛的定义；2、一致收敛级数的判别法——魏尔斯特拉斯判别法；4、幂级数的一致收敛性．3、一致收敛级数的基本性质； 练习题 练习题答案第十章习题课 常数项级数函数项级数一般项级数正项级数幂级数三角级数收敛半径R泰勒展开式数或函数函数数任意项级数泰勒级数在收敛级数与数条件下相互转化一、主要内容 1、常数项级数级数的部分和定义级数的收敛与发散 性质1:级数的每一项同乘一个不为零的常数,敛散性不变.性质2:收敛级数可以逐项相加与逐项相减.性质3:在级数前面加上有限项不影响级数的敛散性.性质4:收敛级数加括弧后所成的级数仍然收敛于原来的和.级数收敛的必要条件:收敛级数的基本性质 常数项级数审敛法正项级数任意项级数1.2.4.充要条件5.比较法6.比值法7.根值法4.绝对收敛5.交错级数(莱布尼茨定理)3.按基本性质;一般项级数4.绝对收敛 定义2、正项级数及其审敛法审敛法(1)比较审敛法 (2)比较审敛法的极限形式 定义正、负项相间的级数称为交错级数.3、交错级数及其审敛法 定义正项和负项任意出现的级数称为任意项级数.4、任意项级数及其审敛法 5、函数项级数(1)定义(2)收敛点与收敛域 (3)和函数 (1)定义6、幂级数 (2)收敛性 推论 定义:正数R称为幂级数的收敛半径.幂级数的收敛域称为幂级数的收敛区间. a.代数运算性质:加减法(其中(3)幂级数的运算 乘法(其中除法 b.和函数的分析运算性质: 7、幂级数展开式(1)定义 (2)充要条件(3)唯一性 (3)展开方法a.直接法(泰勒级数法)步骤:b.间接法根据唯一性,利用常见展开式,通过变量代换,四则运算,恒等变形,逐项求导,逐项积分等方法,求展开式. (4)常见函数展开式 (5)应用a.近似计算b.欧拉公式 二、典型例题例1解 根据级数收敛的必要条件，原级数收敛． 解根据比较判别法，原级数收敛． 解从而有 原级数收敛；原级数发散；原级数也发散． 例２解即原级数非绝对收敛． 由莱布尼茨定理： 所以此交错级数收敛，故原级数是条件收敛． 例３解两边逐项积分 例4解 例5解 测验题 测验题答案 '