- 2.21 MB
- 2022-04-29 14:37:19 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'3磨削几何学与动力学3.1引言与车削、铣削等加工方法相比,磨削时参与加工的磨粒多,每个磨粒几何形状各异,每个磨粒相对于工件的位置和方向是随机的。因此,研究磨削几何学不可能象研究切削几何学那样有着固定的角度,只能采用平均的方法或统计的方法。
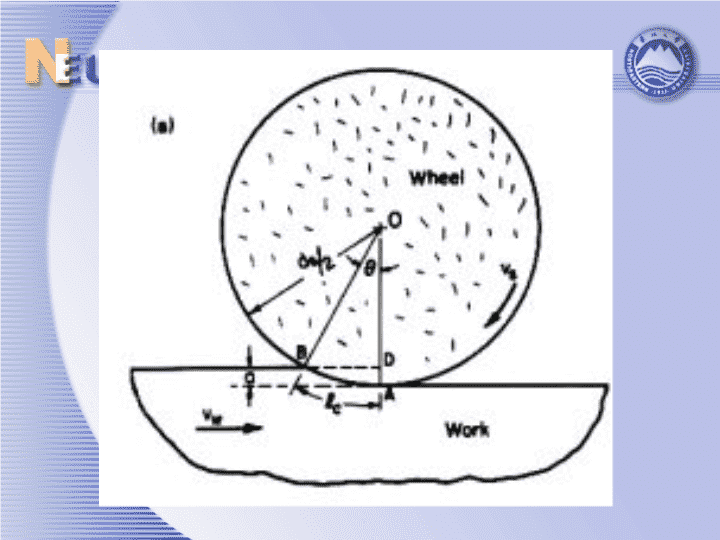
3.2砂轮-工件的几何接触长度平面、外圆和内圆磨削的几何特征如图所示。对于平面磨削,直径为的砂轮以速度旋转,并以速度相对工件移动,砂轮对工件的切深为a。外圆磨削和内圆磨削的情况与此类似,只是相对工件的运动速度是由工件的转动而不是移动形成的。
平面磨削的砂轮切深等于机床的向下进给量,而内外圆磨削的砂轮切深则等于工件转一转径向进给速度实现的径向进给量()。内外圆磨削的磨削深度一般为2~20m,平面磨削磨削深度一般为10~50m。通常砂轮速度为30m/s,在一些特殊场合也可达更高,对难加工材料则可能使用较低的砂轮速度。工件进给速度要低于砂轮速度。在我国,砂轮速度与工件速度的比值通常为60~100。在国外,平面磨削中的比值通常在100~200的范围内,而内外圆磨削则在50~100的范围内。
砂轮切入工件会产生一个接触作用区域,这一接触区域的弧长用表示。如不计砂轮和工件的运动和变形,各种磨削形式的接触弧长可以统一表示为:对于平面磨削有:
因为,而且对小角度近似可得到:由于未计运动和变形,因此参数通常被称为静态接触长度。实际上是将接触弧长用弦长AB表示。
在外圆磨削和内圆磨削中,如果同样象平面磨削那样将内外圆磨削的接触长度近似为弦长AB。这时有:由外圆磨削几何学得到:对于内圆磨削,则有
所以平面磨削、外圆磨削和内圆磨削可以用同一种简单统一的形式表达:其中称为“砂轮当量直径”,被定义为:分母中的加号用于外圆磨削,减号用于内圆磨削,而对于平面磨削因,因此有。
外圆磨削中砂轮当量直径总是小于。对于内圆磨削,当量直径总是大于。一般由于磨削条件的不同,磨削接触长度将在0.1mm~10mm的范围内变化。
3.3磨粒切削路径为分析切削几何,把砂轮的作用比拟为铣刀,而把切刃看作是铣刀刀齿。在该理想化砂轮上,切刃沿砂轮圆周方向以间隔L均匀排列。这时平面磨削(相当于卧轴平面铣削)的情况如下图所示。
外圆磨削中如下图所示。
磨削区中当砂轮速度和工件进给速度方向相反时,称这种磨削方式为逆磨(up-grinding);两方向若相同则称为顺磨(down-grinding)。设逆磨时切刃在F’点与工件开始接触,经过曲线路径到达A’点;顺磨时切刃则从A’点到F’点。相对于工件而言的切削路径FBCA是砂轮圆周速度和工件进给速度的切向速度合成的一条摆线。前一个切刃的切削路径沿工件表面平移的距离AA等于转过相邻切刃间隔时间内的工件平移量s,可用工件进给速度乘以两次连续切削间隔时间()的乘积表示,即:
对于平面磨削,相对于原点在B点的固定于工件上的X-Y坐标系,当砂轮转过角时,在原点的切刃沿摆线轨迹在水平方向的运动为(式中“+”号用于逆磨,“-”号用于顺磨):而在垂直方向为:
由于很小,上式可以简化为:消掉以后可得磨粒切削路径方程为:即用抛物线方程近似代替摆线方程。
对外圆和内圆磨削也可导出和平面磨削相似的切削路径方程,其摆线路径可以用抛物线方程近似:对外圆磨削:
对内圆磨削:式中有两个符号的地方,上面的符号用于逆磨,下面的符号用于顺磨。对于平面磨削,用代入即可。
由切削路径方程可以求出平面磨削切削路径FBA的长度。因为在各种情况下FB的长度可认为等于转过相邻磨粒时间内的进给量s的一半,切削路径总长度可表示为:其中
最后可得:因为为小角度,其二次量与一次量比较可以忽略不计,另外与弧长AB对应的可以近似等于弦长,所以有:
或写成由于Vw与Vs相比很小,在总切削路径长度中s/2占的比例很小并可忽略不计,这时得到:一般情况下,可以认为切削路径长度就等于接触长度。
3.4磨粒最大切削深度(未变形切削厚度)一个切刃的最大切削深度(未变形切屑厚度)用表示。对于一个切刃均匀等距地分布在外圆周表面的理想砂轮而言,的表达式可以由其抛物线形切削路径求出。但这一分析过程非常复杂,并且其物理含义也不明确。为方便计,可将各种磨削的切削路径用一段圆弧来近似。这意味着工件进行间断地运动,在一个切刃进行切削时工件是静止不动的,而在下一个切刃开始切入之前则突然移动一个距离OO。对于平面磨削,该最大未变形切屑厚度对应于AC的长度,所以有:
为计算未变形切屑厚度,我们需要知道两连续切刃的间隔L。我们经常通过测量砂轮地貌获得单位砂轮面积上的切刃数C,并需要导出一个换算公式。如果每一切刃的平均有效切削宽度为,砂轮圆周任一周线上的切刃数K等于砂轮周长与有效切削宽度乘积的C倍,即由于,所以。
有效平均宽度取决于最大未变形切屑厚度和它垂直于切削路径的截面形状。为简化计,将未变形切屑厚度看成矩形,其宽度假定和平均未变形切屑厚度成比例:对于的情况,平均未变形切屑厚度是最大切削厚度的一半,所以
综合后可得
3.5磨粒未变形切削厚度的另一种分析方法另一种计算未变形切屑厚度的近似方法是基于切刃产生的切屑的体积和去除率间的平衡。单位时间内产生的切屑数和每一切屑体积的乘积等于体积去除率,即其中是砂轮宽度上单位时间作用的切刃数,是每一切屑体积,是体积去除率。对于形状切屑及的情况,切屑体积是切屑平均截面积和长度的积:
因此得对于矩形截面切屑,综合后可得对于三角形截面切屑,令r为切削路径任意点处切屑宽度与厚度之比,则未变形切屑可看成一三棱锥,此时,切屑体积为
此时最大未变形切屑厚度为:比较两式,可以看出后者数值略大,但影响因素及其影响趋势是相同的。
3.6不均匀的砂轮地貌前面在推导单颗磨粒的未变形切屑厚度时,我们有过砂轮表面的磨粒是“等高、等间距”的假设,但对于实际的砂轮,上述假设是过于理想化了,只能看作是一种平均的结果。据观察研究,砂轮表面的磨粒在周向和轴向上服从以某数值为中心的均匀分布,在径向上服从某参数的正态分布。因此在砂轮表面上,有的磨粒由于高度低而可能不产生切削作用。即并不是砂轮表面的每一个磨粒都会产生切削作用的,那些能够产生切削作用的磨粒称为有效磨粒。
平面磨削中砂轮地貌不均匀的影响如上图所示。当三个不均匀间隔、不等高度的磨粒依次对工件进行切削时,其切深分别为a0、a1、a2,图中a0>a1,对应砂轮中心在O1处的磨刃突出高度比前一个磨刃低δ1,因此该磨刃的未变形切削厚度相应地要小δ1,即
3.7往复磨削
3.8其他几种磨削形式3.8.1砂轮表面倾斜的斜平面磨削
3.8.2轮廓磨削(成形磨削)
3.8.3角度磨削
3.8.4螺旋槽磨削
3.8.5端面磨削
3.8.6立轴平面磨削
3.8.7切断磨削'