《期中必修1复习2》课件PPT(人教版必修1) 41页

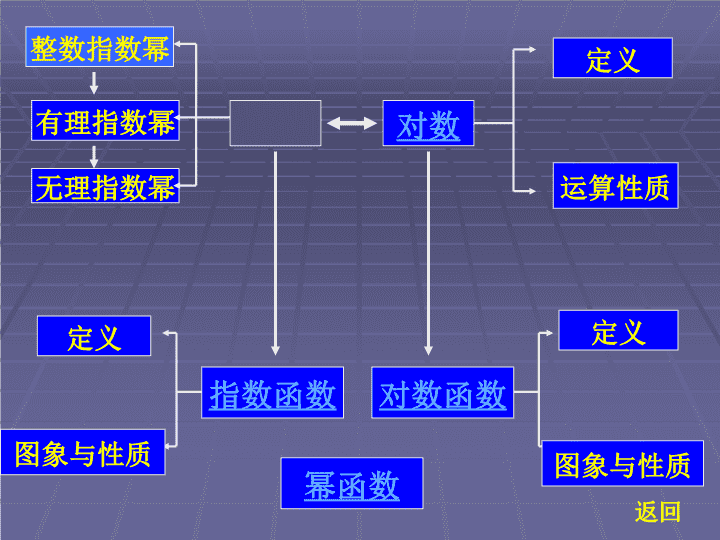
'期中必修１复习第二课时 第二章基本初等函数Ⅰ指数函数对数函数幂函数 整数指数幂有理指数幂无理指数幂指数对数定义运算性质指数函数对数函数幂函数定义图象与性质定义图象与性质返回 （一）指数幂与根式运算1.指数幂的运算性质 2.a的n次方根如果　　　，(n>1,且n),那么x就叫做a的n次方根．(1)当n为奇数时，a的n次方根为,其中(2)当n为偶数时，a>0时，a的n次方根为　　；a<0时，a的n次方根不存在． 3.根式！根式　　对任意实数a都有意义，！当n为正奇数时，　　　　，！当n为正偶数时， 4.分数指数幂(1)正数的分数指数幂：(2)零的正分数指数幂为零，零的负分数指数幂没有意义 (a>0，)！负数和零没有对数.！常用关系式：（二）对数的概念及运算1.概念 (1)(2)(3)(a>0,且a≠1,M>0,N>0)2.对数运算性质 3.几个重要公式(换底公式) 图象a>100时,y>1;x<0时,00时,01指数函数的图像与性质 图象性质对数函数y=logax(a＞0,且a≠1)a＞10＜a＜1定义域:(0,+∞)值域:R过点(1,0),即当x＝1时,y＝0在(0,+∞)上是增函数在(0,+∞)上是减函数yx0yx0(1,0)(1,0)当x>1时，y>0当x=1时，y=0当01时，y<0当x=1时，y=0当00 a>1a>111RR(0,+∞)(0,+∞)(0,1)(1,0)01X<0X>001y<0y>0增函数增函数 xoy 指数函数与对数函数（互为反函数） 指数函数与对数函数（互为反函数） {x︳x＞且x≠}例1求定义域(1)y=log(5x-1)(7x-2)的定义域是(2)y=的定义域是题型一：求定义域 例2比较下列各题中两数值的大小(1)1.72.5,1.73.(2)0.8-0.1,0.8-0.2(3)(4)题型二：比较大小（单调性的应用） 比较两个幂的形式的数大小的方法:(1)对于底数相同指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断.(2)对于底数不同指数相同的两个幂的大小比较,可以利用比商法来判断.(3)对于底数不同指数也不同的两个幂的大小比较,则应通过中间值来判断.常用的中间值是0，11和0. 例3比较下列各组数中两个值的大小：(1)log23.4,log28.5;(2)log0.31.8,log0.32.7;(4)log67,log76;(3)log3,log20.8. 比较大小的方法(1)利用函数单调性(同底数)(2)利用中间值（如:0,1.）(3)变形后比较(4)作差比较 题型三：图像过定点（2）函数恒过定点(1,3)则b=___.例4（1）函数恒过定点________. 例5（1）满足不等式的x的取值范围是_________.（2）解不等式题型四：解不等式（单调性的应用）（3）解不等式（4）解不等式（5）解不等式 例6（1）已知3lg(x－3)＜1,求x的范围.（2）已知logm5>logn5,试确定m和n的大小关系. 题型五：函数奇偶性的判断 题型六：综合问题 换元法 3.函数y=xα叫做幂函数，其中x是自变量，α是常数. 第三章函数的应用函数与方程函数模型及其应用 y=f(x)的图像与x轴的交点的横坐标叫做该函数的零点。即f(x)=0的解。方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点（一）函数的零点与方程的根 结论xy0ab..零点存在定理(1)函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线：(2)f(a)·f(b)<0函数y=f(x)在区间(a,b)内至少有一个零点； 一元二次方程ax2+bx+c=0（a>0）的根的分布一般情况两个根都小于K两个根都大于K一个根小于K，一个根大于Kyxkkk一个根正，一个根负f(k)<0f(0)<0,正根大f(0)<0且 一元二次方程ax2+bx+c=0（a>0）的根的分布一般情况两个根有且仅有一个在（k.k)内12x1∈(m,n)x2∈(p,q)两个根都在（k.k)内21yxkk12kk12mnpqf(k)f(k)<012 对于在区间上连续不断且的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).二分法概念xy0ab 用二分法求方程近似解的步骤:,给定精确度；⑴确定区间[a,b],验证⑵求区间(a,b)的中点；⑶计算若f()=0，则就是函数的零点；②若，则令b=()；此时零点③若，则令a=(此时零点)；⑷判断是否达到精确度：即若|a-b|<,则得到零点近似值为a(或b);否则重复⑵~⑷总结提炼 选初始区间取区间中点中点函数值为零结束是定新区间否区间长度小于精确度否是 （二）函数模型及其应用不同增长的函数模型函数模型应用实例 祝同学们期中考试取得好成绩！'