微波技术课件PPT88934693.ppt 13页

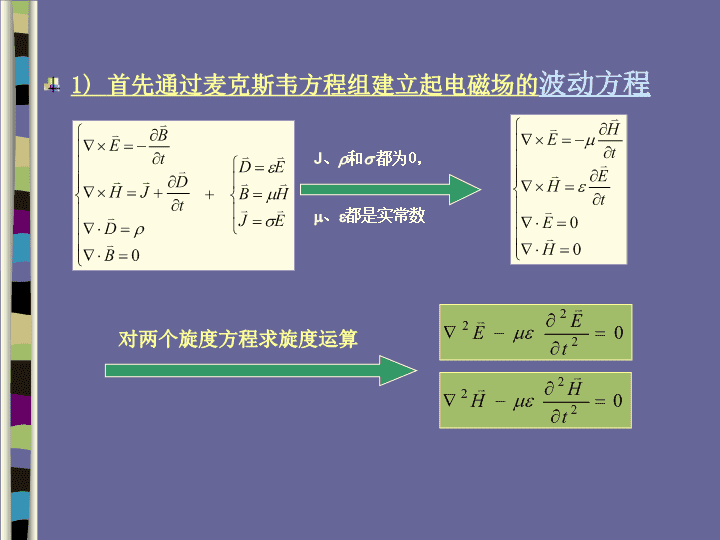
'第三章规则波导波导通常专指——波导管广义地指——能够引导电磁波传播的装置比如双导线、同轴线、微带线、介质传输线等均可称为波导。也可以统称为传输线。其作用都是导引电磁波沿一定方向传播被导引的电磁波称为导行波，这些传输线称导波系统，简称导波规则波导指沿轴向方向，横截面的形状、尺寸，以及填充介质的分布状态和电参数均不变化的无限长的直波导。 §3-1波动方程与导行波为使问题更简单化并考虑实用性，作如下假设：波导内壁是理想导电面（＝）波导内为理想介质（、为实数常数）波导内为无源区域(ρ=0,J=0)，且远离波源。波导中的场随时间作简谐变化，可用复数形式表示波导无限长研究波导中的电磁场问题，实质上就是求满足波导内壁边界条件的Maxwell方程组 1)首先通过麦克斯韦方程组建立起电磁场的波动方程J、和都为0，、都是实常数对两个旋度方程求旋度运算 2)时间和空间变量分离对于简谐场，可用复矢量形式表示 坐标系的选择采用广义的正交（柱）坐标系（u,v,z）此时可将场量分解为横向分量和纵向分量，纵向和横向变量分离其中，E(u,v)仅是横向坐标(u,v)的函数，它表示电场在波导横截面内的分布状态，称为分布函数，Z(z)仅是坐标z的函数，它表示电场沿z轴的分布规律，称为传播因子。 将Laplace算子分离为横向和纵向两部分h1和h2与坐标z无关，且h3＝1已知广义正交坐标系下，其中： 利用变量分离对复矢量波动方程处理应为常数是传播常数，=+j理想：＝0,=j令亥姆霍兹方程 §3-1波动方程与导行波——导行电磁波通过对纵向坐标z，进行分离变量。由此可以得到两个方程。是传播常数，=+j；理想：＝0,=j，此时理想：Kc2＝k2-2K＝KC时，=0，波不再沿z轴传播，称截止状态;KC称为截止波数Kc大小与波导横截面的形状、尺寸，以及所传输的波型有关。(1)一个是关于z的二阶常微分方程,其通解就是导行波的一般形式。 (2)另一方程是E和H关于u，v两个变量的二阶偏微分方程将E和H两个空间矢量（都有u,v,z三个分量）分解为6个分量，得到标量形式亥姆霍兹方程6个分量不是完全独立的,因为需满足Maxwell方程中的两个旋度方程若将两个纵向分量Ez和Hz作为独立变量，再利用麦克斯韦方程中的旋度关系,就可以导出各横向分量与纵向分量之间的关系。 将场量写出纵向和横向分量应满足Maxwell旋度方程横向分量与纵向分量之间的关系取式(1)两端的横向分量：同理，取式(2)两端的横向分量，可得： 式(4)两端同时用z叉乘 整理得：两边同除以Kc2类似可得： 若波导是无耗的，即＝j，kc2=k2-2,则可见，只要求出Ez和Hz，则场的横向分量即可求出，每一种波型的场的分布状态也就求出来了。'