最新斯托克斯定理课件PPT.ppt 33页

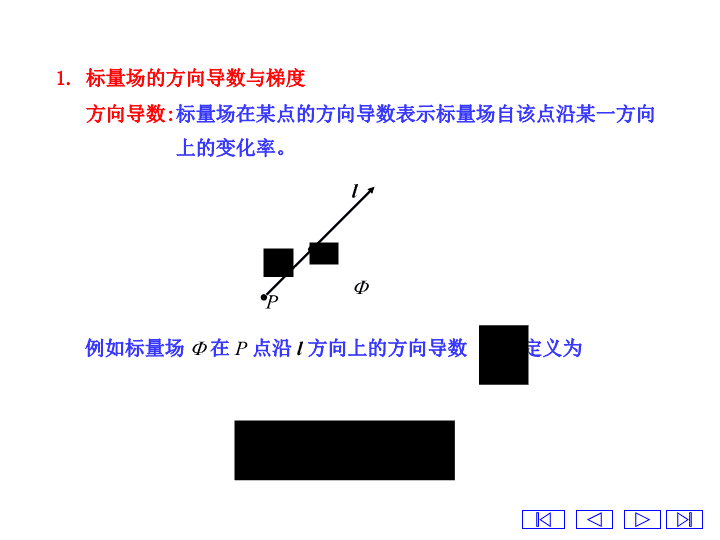
'斯托克斯定理 1.标量场的方向导数与梯度方向导数:标量场在某点的方向导数表示标量场自该点沿某一方向上的变化率。例如标量场在P点沿l方向上的方向导数定义为Pl 梯度:标量场在某点梯度的大小等于该点的最大方向导数，梯度的方向为该点具有最大方向导数的方向。可见，梯度是一个矢量。在直角坐标系中，标量场的梯度可表示为式中grad是英文字母gradient的缩写。若引入算符，它在直角坐标系中可表示为则梯度可表示为 因此散度可用算符表示为高斯定理或者写为从数学角度可以认为高斯定理建立了面积分和体积分的关系。从物理角度可以理解为高斯定理建立了区域V中的场和包围区域V的闭合面S上的场之间的关系。因此，如果已知区域V中的场，根据高斯定理即可求出边界S上的场，反之亦然。 环量：矢量场A沿一条有向曲线l的线积分称为矢量场A沿该曲线的环量，以表示，即3.矢量场的环量与旋度可见，若在闭合有向曲线l上，矢量场A的方向处处与线元dl的方向保持一致，则环量>0；若处处相反，则<0。可见，环量可以用来描述矢量场的旋涡特性。 由物理学得知，真空中磁感应强度B沿任一闭合有向曲线l的环量等于该闭合曲线包围的传导电流强度I与真空磁导率0的乘积。即式中电流I的正方向与dl的方向构成右旋关系。由此可见，环量可以表示产生具有旋涡特性的源的强度，但是环量代表的是闭合曲线包围的总的源强度，它不能显示源的分布特性。为此，需要研究矢量场的旋度。 旋度：旋度是一个矢量。若以符号rotA表示矢量A的旋度，则其方向是使矢量A具有最大环量强度的方向，其大小等于对该矢量方向的最大环量强度，即式中rot是英文字母rotation的缩写，en为最大环量强度的方向上的单位矢量，S为闭合曲线l包围的面积。上式表明，矢量场的旋度大小可以认为是包围单位面积的闭合曲线上的最大环量。 直角坐标系中旋度可用矩阵表示为或用算符表示为应该注意，无论梯度、散度或旋度都是微分运算，它们表示场在某点附近的变化特性，场中各点的梯度、散度或旋度可能不同。因此，梯度、散度及旋度描述的是场的点特性或称为微分特性。函数的连续性是可微的必要条件。因此在场量发生不连续处，也就不存在前面定义的梯度、散度或旋度。 斯托克斯定理同高斯定理类似，从数学角度可以认为斯托克斯定理建立了面积分和线积分的关系。从物理角度可以理解为斯托克斯定理建立了区域S中的场和包围区域S的闭合曲线l上的场之间的关系。因此，如果已知区域S中的场，根据斯托克斯定理即可求出边界l上的场，反之亦然。或者写为 散度处处为零的矢量场称为无散场，旋度处处为零的矢量场称为无旋场。4.无散场和无旋场两个重要公式：左式表明，任一矢量场A的旋度的散度一定等于零。因此，任一无散场可以表示为另一矢量场的旋度，或者说，任何旋度场一定是无散场。右式表明，任一标量场的梯度的旋度一定等于零。因此，任一无旋场一定可以表示为一个标量场的梯度，或者说，任何梯度场一定是无旋场。 5.格林定理设任意两个标量场及，若在区域V中具有连续的二阶偏导数，如下图示。SV,那么，可以证明该两个标量场及满足下列等式根据方向导数与梯度的关系，上式又可写成式中S为包围V的闭合曲面，为标量场在S表面的外法线en方向上的偏导数。上两式称为标量第一格林定理。 基于上式还可获得下列两式：上两式称为标量第二格林定理。设任意两个矢量场P与Q，若在区域V中具有连续的二阶偏导数，那么，可以证明该矢量场P及Q满足下列等式式中S为包围V的闭合曲面，面元dS的方向为S的外法线方向，上式称为矢量第一格林定理。 基于上式还可获得下式：此式称为矢量第二格林定理。无论何种格林定理，都是说明区域V中的场与边界S上的场之间的关系。因此，利用格林定理可以将区域中场的求解问题转变为边界上场的求解问题。此外，格林定理说明了两种标量场或矢量场之间应该满足的关系。因此，如果已知其中一种场的分布特性，即可利用格林定理求解另一种场的分布特性。格林定理广泛地用于电磁理论。 6.矢量场的唯一性定理位于某一区域中的矢量场，当其散度、旋度以及边界上场量的切向分量或法向分量给定后，则该区域中的矢量场被惟一地确定。已知散度和旋度代表产生矢量场的源，可见唯一性定理表明，矢量场被其源及边界条件共同决定的。 若矢量场F(r)在无限区域中处处是单值的，且其导数连续有界，源分布在有限区域V中，则当矢量场的散度及旋度给定后，该矢量场F(r)可以表示为7.亥姆霍兹定理式中可见，该定理表明任一矢量场均可表示为一个无旋场与一个无散场之和。矢量场的散度及旋度特性是研究矢量场的首要问题。 8.正交曲面坐标系已知矢量A在圆柱坐标系和球坐标系中可分别表示为式中a,b,c均为常数，A是常矢量吗？圆柱(r,,z)yzxP00=0r=r0z=z0Oxzy=000球(r,,)r=r0=0P0O直角(x,y,z)zxyz=z0x=x0y=y0P0O 任务二用拍痧为“患者”实施康复治疗聊城职业技术学院康复教研室学习情境一：用刮痧为“患者”实施康复治疗 1.课前预习2.案例导入3.模拟治疗4.总结评价5.布置作业6.见习实习教学活动设计 一、课前预习同学们通过查阅相关资料，小组学习，已经初步掌握拍痧的基本知识。这次课我们的教学目标是1.说出拍痧的概念；2.阐明拍痧疗法的作用机理；3.描述拍痧的操作要领；4.分析判断适应症和禁忌症；5.概括拍痧法注意事项。熟练为“患者”实施拍痧治疗。知识目标技能目标 二、案例导入案例：耿某，男，46岁。患白塞氏三联证，皮肤不像皮样、内粘膜重度溃疡、说话别人听不懂、偏瘫行动困难、胳膊伸不开、手指不会动、高血压。学习任务：1.该病人的中医诊断是什么？2.该病人可以用拍痧治疗吗？如可以，如何进行治疗？如不可以，应采取什么治疗方法？ 三、模拟治疗步骤一：诊断、辨证通过拍痧起到化湿热解毒之功。本案例患者的中医诊断为狐惑病。本病案患者患有白塞氏综合征，和中医的狐惑病相似，多由感受湿热毒气，或因热病后期，余热未尽，或脾虚湿浊之邪内生等致湿热毒邪内蕴，病及血分，毒瘀互结。可以用拍痧治疗。 三、模拟治疗步骤二：拍痧准备1.选择工具：橡胶式拍痧掌。（拍痧工具主要有竹条式拍痧棒和橡胶式拍痧掌，灵活选用。）2.消毒：橡胶式拍痧掌的消毒、术者手指消毒（75%乙醇棉球涂擦）、施术部位消毒（在所选穴位上用75%乙醇棉球从中心向外圈试擦）。 三、模拟治疗步骤二：拍痧准备3.选择体位：根据所拍部位的变化，不断变化体位。（选择体位以术者能正确取穴、便于手法操作，同时患者感觉舒适为原则。临床常用体位有卧位和坐位。卧位又可分为仰卧位、侧卧位、俯卧位，坐位又可分为仰靠坐位、侧伏坐位、俯伏坐位。） 三、模拟治疗步骤三：模拟治疗手执一只橡胶拍痧掌对全身的皮肤施拍，施拍力度灵活掌握，在身体的某一点施拍至出痧后，随即挨着排的往下移动着拍下去，这样一点不漏地一直拍到全身出透痧(也可局部施治)。 三、模拟治疗步骤四：拍痧后给予患者健康指导从拍完这天起需15天为吸收恢复期,15天后即可完全恢复正常。一疗程大约需要25-30天，视不同病症决定需要几个疗程可治疗痊愈。 四、总结、评价拍痧是中国古老的保健、治病方法之一，其具体方法就是用手掌或借助工具反复拍打身体患病部位直至出“痧”程度，从而达到治病、保健的目的。应严格掌握其适应症、禁忌症和注意事项。根据课前查阅材料及课堂操作体会，总结出拍痧的适应症、禁忌症、注意事项。总结 四、总结、评价同学们，请根据你们的发言情况和实际操作技能的熟练程度对同学们进行评价。课下继续练习，准备技能考核。评价成绩包括学生互评、教师评价、技能考核三部分，将评价成绩计入期末考试总成绩。评价 五、布置作业1.自学扯痧法、焠痧法。2.预习：用揪痧法为“患者”实施康复治疗，通过查阅资料、小组学习，初步掌握揪痧法的基本知识。 六、临床见习实习在学院教学医院，康复科教师把同学们分组带入康复病房介绍拍痧法病人大致情况，学生扮演康复治疗师，在教师指导下为患者实施拍痧。 谢谢！'