【精品】《二次函数》中考总复习PPT课件PPT课件精品课件 114页

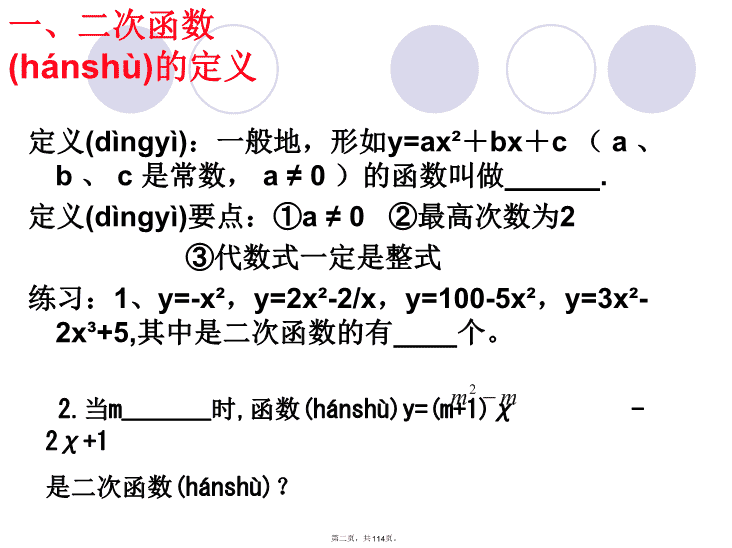
'第一页，共114页。 一、二次函数(hánshù)的定义定义(dìngyì)：一般地，形如y=ax²＋bx＋c（a、b、c是常数，a≠0）的函数叫做______.定义(dìngyì)要点：①a≠0②最高次数为2③代数式一定是整式练习：1、y=-x²，y=2x²-2/x，y=100-5x²，y=3x²-2x³+5,其中是二次函数的有____个。2.当m_______时,函数(hánshù)y=(m+1)χ-2χ+1是二次函数(hánshù)？第二页，共114页。 3、下列函数(hánshù)中哪些是一次函数(hánshù)，哪些是二次函数(hánshù)？巩固(gǒnggù)一下吧！第三页，共114页。 1，函数（其中a、b、c为常数），当a、b、c满足(mǎnzú)什么条件时，（1）它是二次函数；（2）它是一次函数；（3）它是正比例函数；当时，是二次函数；当时，是一次函数；当时，是正比例函数；驶向胜利的彼岸考考你第四页，共114页。 驶向胜利的彼岸2，函数当m取何值时，（1）它是二次函数(hánshù)？（2）它是反比例函数(hánshù)？（1）若是二次函数，则且∴当时，是二次函数。（2）若是反比例函数，则且∴当时，是反比例函数。第五页，共114页。 小结(xiǎojié)：1.二次函数y=ax²+bx+c(a,b,c是常数,a≠0)的几种不同表示形式:(1)y=ax²(a≠0,b=0,c=0,).(2)y=ax²+c(a≠0,b=0,c≠0).(3)y=ax²+bx(a≠0,b≠0,c=0).（4)y=a(x-h)2(a≠0)(5)y=a(x-h)2+k(a≠0)2.定义的实质是：ax²+bx+c是整式,自变量x的最高次数是二次,自变量x的取值范围是全体实数.各种形式的特征第六页，共114页。 二、二次函数(hánshù)的图象及性质抛物线顶点(dǐngdiǎn)坐标对称轴位置(wèizhi)开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定a>0,开口向上a<0,开口向下在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.xy0xy0(0,c)(0,c)第七页，共114页。 抛物线开口方向对称轴顶点坐标a>0a<0y=axy=ax+ky=a(x-h)y=a(x-h)+k小结(xiǎojié)：222开口向下开口向上y轴(直线(zhíxiàn)x=0)直线(zhíxiàn)x=h(0,0)(0,k)(h,0)(h,k)当|a|的值越大时，抛物线开口越小，函数值y变化越快。当|a|的值越小时，抛物线开口越大，函数值y变化越慢。只要a相同，抛物线的形状（开口大小和开口方向）就相同。第八页，共114页。 点评：二次函数的几种(jǐzhǒnɡ)表现形式及图像①、②、③、④、⑤、(顶点(dǐngdiǎn)式)(一般(yībān)式)xyo第九页，共114页。 1.如图,抛物线y=ax2+bx+c,请判断下列(xiàliè)各式的符号：①a0;②c0;③b2-4ac0;④b0;xyO基础(jīchǔ)演练变式1：若抛物线的图象如图，则a=.变式2：若抛物线的图象如图，则△ABC的面积是。ABC小结：a决定开口方向(fāngxiàng)，c决定与y轴交点位置，b2-4ac决定与x轴交点个数，a,b结合决定对称轴;第十页，共114页。 ABCD2、下列各图中可能是函数与()的图象的是()小结：双图象的问题，寻找自相矛盾的地方。即由一个图象得出字母的取值范围(fànwéi)，再去检验这个字母的符号是否适合另一个图象√第十一页，共114页。 3、画二次函数y=x2-x-6的图象(túxiànɡ)，顶点坐标是__________对称轴是_________。（—，-—）12524x=—12画二次函数的大致图象:先配成顶点式，再按照以下步骤画：①画对称轴②确定顶点③确定与y轴的交点④确定与x轴的交点⑤确定与y轴交点关于对称轴对称的点⑥连线当然，细画抛物线应该按照：列表（在自变量的取值范围内列）、描点（要准）、连线（用平滑(pínghuá)的曲线）三步骤来画。x=—12（—，-—）12524(0,-6)(-2,0)(3,0)0xy(1,-6)特别注意：在实际问题中画函数的图像时要注意自变量的取值范围，若图像是直线(zhíxiàn)，则画图像时只取两个界点坐标来画（包括该点用实心点，不包括该点用空心圈);若是二次函数的图像，则除了要体现两个界点坐标外，还要取上能体现图像特征的其它一些点来画第十二页，共114页。 3、二次函数(hánshù)y=x2-x-6的图象顶点坐标是__________对称轴是_________。（—，-—）12524x=—12x=—12（—，-—）12524(0,-6)(-2,0)(3,0)0xy(1,-6)增减(zēnɡjiǎn)性:当时,y随x的增大(zēnɡdà)而减小当时,y随x的增大(zēnɡdà)而增大(zēnɡdà)最值:当时,y有最值,是小函数值y的正负性:当时,y>0当时,y=0当时,y<0x<-2或x>3x=-2或x=3-20？已知二次函数(hánshù)第十五页，共114页。 2、已知抛物线顶点(dǐngdiǎn)坐标（h,k）和一个普通点，通常设抛物线解析式为_______________3、已知抛物线与x轴的两个交点(x1,0)、(x2,0)和另一个普通点,通常(tōngcháng)设解析式为_____________1、已知抛物线上的三个普通点，通常(tōngcháng)设解析式为________________y=ax2+bx+c(a≠0)y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2)(a≠0)三、求抛物线解析式的三种方法第十六页，共114页。 练习(liànxí)1、二次函数y=x2+2x+1写成顶点式为：__________，对称轴为_____，顶点为______12y=(x+2)2-112x=-2(-2，-1)2、已知二次函数y=-x2+bx-5的图象的顶点在y轴上，则b=___。120第十七页，共114页。 3、根据下列条件，求二次函数(hánshù)的解析式。(1)、图象经过(jīngguò)(0，0)，(1，-2)，(2，3)三点；(2)、图象(túxiànɡ)的顶点(2，3)，且经过点(3，1)；(3)、图象经过(0，0)，(12，0)，且最高点的纵坐标是3。第十八页，共114页。 4、已知二次函数y=ax2+bx+c的最大值是2，图象(túxiànɡ)顶点在直线y=x+1上，并且图象(túxiànɡ)经过点（3，-6）。求a、b、c。解：∵二次函数(hánshù)的最大值是2∴抛物线的顶点纵坐标为2又∵抛物线的顶点在直线y=x+1上∴当y=2时，x=1∴顶点坐标为（1，2）∴设二次函数(hánshù)的解析式为y=a(x-1)2+2又∵图象经过点（3，-6）∴-6=a(3-1)2+2∴a=-2∴二次函数(hánshù)的解析式为y=-2(x-1)2+2即：y=-2x2+4x第十九页，共114页。 abc2a+b2a-bb2-4aca+b+ca-b+c4a+2b+c4a-2b+c开口方向、大小:向上(xiàngshàng)a>0向下ao负半轴c<0，过原点c=0.-与1比较-与-1比较与x轴交点个数令x=1，看纵坐标令x=-1，看纵坐标令x=2，看纵坐标令x=-2，看纵坐标四、有关a，b，c及b2-4ac符号的确定第二十页，共114页。 快速(kuàisù)回答：抛物线y=ax2+bx+c如图所示，试确定(quèdìng)a、b、c、△的符号：xoy第二十一页，共114页。 抛物线y=ax2+bx+c如图所示，试确定(quèdìng)a、b、c、△的符号：xyo快速(kuàisù)回答：第二十二页，共114页。 抛物线y=ax2+bx+c如图所示，试确定(quèdìng)a、b、c、△的符号：xyo快速(kuàisù)回答：第二十三页，共114页。 抛物线y=ax2+bx+c如图所示，试确定(quèdìng)a、b、c、△的符号：xyo快速(kuàisù)回答：第二十四页，共114页。 抛物线y=ax2+bx+c如图所示，试确定(quèdìng)a、b、c、△的符号：xyo快速(kuàisù)回答：第二十五页，共114页。 典型(diǎnxíng)例题1.如图,是抛物线y=ax2+bx+c的图像，则①a0;②b0;c0;a+b+c0;a-b+c0;b2-4ac0;2a-b0;<<><>>=由形定数(dìnɡshù)第二十六页，共114页。 典型例题2.已知a<0，b>0，c>0，那么(nàme)抛物线y=ax2+bx+c的顶点在（）A.第一象限B.第二(dìèr)象限C.第三象限D.第四象限A由数定形(dìnɡxínɡ)第二十七页，共114页。 1.(河北省)在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图像(túxiànɡ)大致为()B2.(山西省)二次函数(hánshù)y=x2+bx+c的图像如图所示，则函数(hánshù)值y＜0时，对应的x取值范围是.-3＜x＜1.-3-3１点击(diǎnjī)中考:第二十八页，共114页。 3、已知二次函数y=ax2+bx+c的图像如图所示，下列结论(jiélùn)：①a+b+c＜0，②a-b+c＞0；③abc＞0；④b=2a中正确个数为()A.4个B.3个C.2个D.1个A4、无论m为任何实数，二次函数(hánshù)y=x2-(2-m)x+m的图像总是过点()A.(1，3)B.(1，0)C.(-1，3)D.(-1，0)C当x=1时,y=a+b+c当x=-1时,y=a-b+ca<0,b<0,c>0x==-1第二十九页，共114页。 D5.(安徽)二次函数y=ax2+bx+c的图像如图，则下列a、b、c间的关系(guānxì)判断正确的是()A.ab<0B.bc<0C.a+b+c>0D.a-b+c<06.(绵阳)二次函数(hánshù)y=ax2+bx+c的图像如图，则不等式bx+a>0的解为　()A.x>B.x>C.xb④2a+b=0⑤Δ=b-4ac>0第三十四页，共114页。 结论:一般地,抛物线y=a(x-h)2+k与y=ax2形状(xíngzhuàn)相同,位置不同。五、二次函数(hánshù)抛物线的平移温馨(wēnxīn)提示：二次函数图象间的平移，可看作是顶点间的平移，因此只要掌握了顶点是如何平移的，就掌握了二次函数图象间的平移.第三十五页，共114页。 0224-2-4-24262xyy=x2-1y=x2y=x2向下平移(pínɡyí)1个单位y=x2-1向左平移(pínɡyí)2个单位y=(x+2)2y=(x+2)2y=(x+2)2-1(0,0)(-2,-1)●●y=(x+2)2-1上下左右平移抓住顶点(dǐngdiǎn)的变化例：第三十六页，共114页。 平移(pínɡyí)法则：左加右减，上加下减练习⑴二次函数y=2x2的图象向平移个单位(dānwèi)可得到y=2x2-3的图象；二次函数y=2x2的图象向平移个单位(dānwèi)可得到y=2(x-3)2的图象。⑵二次函数y=2x2的图象先向平移个单位(dānwèi)，再向平移个单位(dānwèi)可得到函数y=2(x+1)2+2的图象。下3右3左1上2引申：y=2(x+3)2-4y=2(x+1)2+2第三十七页，共114页。 （3）由二次函数y=x2的图象经过如何(rúhé)平移可以得到函数y=x2-5x+6的图象.y=x2-5x+6y=x2第三十八页，共114页。 （4）将二次函数(hánshù)y=2x2的图像向右平移3个单位后得到函数(hánshù)的图像，其对称轴是，顶点是，当x时，y随x的增大而增大；当x时，y随x的增大而减小.（5）将二次函数(hánshù)y=-3（x-2）2的图像向左平移3个单位后得到函数(hánshù)的图像，其顶点坐标是，对称轴是，当x=___时，y有最值，是.y=2(x-3)2直线(zhíxiàn)x=3(3，0)＞3＜3y=-3(x+1)2(-1，0)直线(zhíxiàn)x=-1-1大0（6）将抛物线y=2x2－3先向上平移3单位，就得到函数的图象，再向平移____个单位得到函数y=2（x-3）2的图象.y=2x2右3第三十九页，共114页。 （7）函数y=3x2+5与y=3x2的图象的不同之处是()A.对称轴B.开口方向C.顶点D.形状4.已知抛物线y=2x2–1上有两点(x1，y1),(x2，y2)且x1＜x2＜0，则y1y2(填“＜”或“＞”)（8）已知抛物线，把它向下平移，得到的抛物线与x轴交于A、B两点，与y轴交于C点，若⊿ABC是直角三角形，那么原抛物线应向下平移几个单位？C第四十页，共114页。 (0,0)(h,k)上下左右平移(pínɡyí)抓住顶点(dǐngdiǎn)的变化!抛物线y=ax2y=a(x-h)2+k记住(jìzhù)：第四十一页，共114页。 六、二次函数(hánshù)与一元二次方程的关系一元二次方程根的情况与b²-4ac的关系我们知道(zhīdào):代数式b2-4ac对于方程的根起着关键的作用.归纳如下：第四十二页，共114页。 判别式：b2-4ac二次函数y=ax2+bx+c（a≠0）图象一元二次方程ax2+bx+c=0（a≠0）的根xyO与x轴有两个(liǎnɡɡè)不同的交点（x1，0）（x2，0）有两个(liǎnɡɡè)不同的解x=x1，x=x2b2-4ac＞0xyO与x轴有唯一(wéiyī)个交点有两个相等的解x1=x2=b2-4ac=0xyO与x轴没有交点没有实数根b2-4ac＜0第四十三页，共114页。 具体(jùtǐ)这样理解：1、当a>0,△>0时，抛物线y=ax2+bx+c与x轴有两个不相同的交点，一元二次方程ax2+bx+c=0有两个不相等的实数根x1、x2(x1x2时，y>0,即ax2+bx+c>0;当x10时，抛物线y=ax2+bx+c与x轴有两个(liǎnɡɡè)不相同的交点，一元二次方程ax2+bx+c=0有两个(liǎnɡɡè)不相等的实数根x1、x2(x10,即ax2+bx+c>0;当xx2时，y<0,即ax2+bx+c<0.y<0第四十四页，共114页。 3、当a>0,△=0时，抛物线y=ax2+bx+c与x轴有两个相同的交点，即顶点在x轴上，一元二次方程ax2+bx+c=0有两个相等的实数(shìshù)根x1、x2(x1=x2)，当x≠x1（或x≠x2）时，y>0,即ax2+bx+c>0;当x=x1=x2时，y=0；无论x取任何实数(shìshù)，都不可能有ax2+bx+c<0.y>0第四十五页，共114页。 4、当a<0,△=0时，抛物线y=ax2+bx+c与x轴有两个(liǎnɡɡè)相同的交点，即顶点在x轴上，一元二次方程ax2+bx+c=0有两个(liǎnɡɡè)相等的实数根x1、x2(x1=x2)，当x≠x1（或x≠x2）时，y<0,即ax2+bx+c<0;当x=x1=x2时，y=0；无论x取任何实数，都不可能有ax2+bx+c>0.y<0第四十六页，共114页。 5、当a<0,△<0时，抛物线y=ax2+bx+c与x轴无交点，即全部(quánbù)图象在x轴的下方，一元二次方程ax2+bx+c=0无实数根，无论x取何值，都有y<0.y<0无论(wúlùn)x取何值，都不可能有y≥0。第四十七页，共114页。 例：已知二次函数(hánshù)y=2x2-(m+1)x+m-1(1)求证：无论m为何(wèihé)值，函数y的图像与x轴总有交点，并指出当m为何(wèihé)值时，只有一个交点。（2）当m为何值时，函数(hánshù)y的图像经过原点。（3）指出（2）的图像中，使y＜0时，x的取值范围及使y＞0时，x的取值范围第四十八页，共114页。 2、求抛物线①与y轴的交点(jiāodiǎn)坐标;②与x轴的两个交点(jiāodiǎn)间的距离.③x取何值时，y＞0?1、不论x为何值时，函数(hánshù)y=ax2+bx+c（a≠0）的值永远为正的条件是____　　　　　_a>0,b²-4ac<0-316(-1,8)-1练习(liànxí)第四十九页，共114页。 3、(1)如果关于x的一元二次方程x2-2x+m=0有两个相等(xiāngděng)的实数根,则m=＿＿＿＿,此时抛物线y=x2-2x+m与x轴有＿＿＿＿个交点.(2)已知抛物线y=x2–8x+c的顶点(dǐngdiǎn)在x轴上,则c=＿＿＿＿.1116(3)一元二次方程3x2+x-10=0的两个(liǎnɡɡè)根是x1=-2,x2=5/3,那么二次函数y=3x2+x-10与x轴的交点坐标是＿＿＿＿.（-2、0）（5/3、0）第五十页，共114页。 4.如图,抛物线y=ax2+bx+c的对称轴是直线(zhíxiàn)x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3,x2=＿＿＿5.已知抛物线y=kx2-7x-7的图象(túxiànɡ)和x轴有交点，则k的取值范围（）-3.3BK≠0b2-4ac≥0第五十一页，共114页。 6.根据下列表格的对应值:判断(pànduàn)方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解x的范围是()A34.（2）卡车可以通过.提示：当x=±2时，y=3,3＋2>4.xy－1－3－1－31313O第一百页，共114页。 （5）投篮(tóulán)与二次函数来到(láidào)操场第一百零一页，共114页。 1、一场篮球赛中，小明跳起投篮，已知球出手时离地面高米，与篮圈中心的水平距离为8米，当球出手后水平距离为4米时到达最大高度4米，设篮球运行(yùnxíng)的轨迹为抛物线，篮圈中心距离地面3米。问此球能否(nénɡfǒu)投中？3米8米4米4米0xy第一百零二页，共114页。 8（4，4）如图，建立(jiànlì)平面直角坐标系，点（4，4）是图中这段抛物线的顶点，因此可设这段抛物线对应的函数为：(0≤x≤8)(0≤x≤8)∵篮圈中心(zhōngxīn)距离地面3米∴此球不能投中第一百零三页，共114页。 若假设出手的角度(jiǎodù)和力度都不变,则如何才能使此球命中?（1）跳得高一点(yīdiǎn)（2）向前平移(pínɡyí)一点第一百零四页，共114页。 yx（4，4）（8，3）在出手角度和力度都不变的情况下,小明(xiǎomínɡ)的出手高度为多少时能将篮球投入篮圈?0123456789第一百零五页，共114页。 yX（8，3）（5，4）（4，4）0123456789在出手角度、力度及高度都不变的情况下，则小明朝着篮球架再向前平移(pínɡyí)多少米后跳起投篮也能将篮球投入篮圈？(７，３）●第一百零六页，共114页。 (0,1.6)2、中考题）推铅球的出手高度为,在如图①求k的值所示的直角坐标系中，铅球的运行(yùnxíng)路线近似为抛物线xyO②求铅球的落点(luòdiǎn)与丁丁的距离③一个1.5m的小朋友跑到离原点6米的地方(dìfāng)(如图)，他会受到伤害吗？来到操场第一百零七页，共114页。 ①求k的值xyO解：解：由图像可知，抛物线过点(0,1.6)即当x=0时，y=1.61.6=-0.1k+2.5K=±3又因为对称轴是在y轴的右侧，即x=k>0所以，k=32②-0.1(x-3)+2.5=0解之得，x=8,x=-2所以，OB=8故铅球的落点与丁丁的距离是8米。221③当x=6时，y=-0.1(6-3)+2.5=1.62>1.5所以(suǒyǐ)，这个小朋友不会受到伤害。B第一百零八页，共114页。 3、如图，一单杠高2.2米，两立柱之间的距离为1.6米，将一根绳子的两端栓于立柱与铁杠(tiěɡànɡ)结合处，绳子自然下垂呈抛物线状。一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离。ABCD0.71.62.20.4EFOxy来到(láidào)操场第一百零九页，共114页。 3、如图，一单杠高2.2米，两立柱(lìzhù)之间的距离为1.6米，将一根绳子的两端栓于立柱(lìzhù)与铁杠结合处，绳子自然下垂呈抛物线状。一身高0.7米的小孩站在离立柱(lìzhù)0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离。ABCD0.71.62.20.4EFOxy来到(láidào)操场第一百一十页，共114页。 3、如图，一单杠高2.2米，两立柱之间的距离(jùlí)为1.6米，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状。一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离(jùlí)。ABCD0.71.62.20.4EFOxy来到(láidào)操场第一百一十一页，共114页。 ABCD0.71.62.20.4EF解：如图，所以(suǒyǐ)，绳子最低点到地面的距离为0.2米.Oxy以CD所在的直线为X轴，CD的中垂线为Y轴建立(jiànlì)直角坐标系，则B（0.8,2.2），F（-0.4,0.7）设y=ax+k,从而有0.64a+k=2.20.16a+k=0.72解得：a=K=0.2258所以，y=x+0.2顶点E（0,0.2）2258第一百一十二页，共114页。 用抛物线的知识解决运动场上或者生活中的一些实际问题(wèntí)的一般步骤：建立(jiànlì)直角坐标系二次函数(hánshù)问题求解找出实际问题的答案及时总结第一百一十三页，共114页。 结束语谢谢(xièxie)大家聆听！！！114第一百一十四页，共114页。'