最新复习课3ppt课件PPT课件 49页

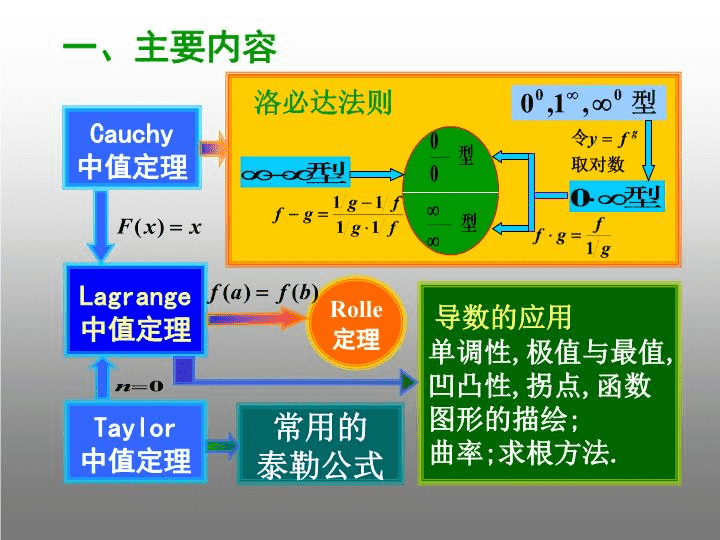
'复习课3ppt课件 第三章微分中值定理及导数的应用习　题　课一.主要内容二.典型例题 常用函数的麦克劳林公式 6、导数的应用定理(1)函数单调性的判定法 定义(2)函数的极值及其求法 定理(必要条件)定义函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点.极值是函数的局部性概念:极大值可能小于极小值,极小值可能大于极大值.驻点和不可导点统称为临界点. 定理(第一充分条件)定理(第二充分条件) 求极值的步骤: 步骤:1.求驻点和不可导点;2.求区间端点及驻点和不可导点的函数值,比较大小,那个大那个就是最大值,那个小那个就是最小值;注意:如果区间内只有一个极值,则这个极值就是最值.(最大值或最小值)(3)最大值、最小值问题 实际问题求最值应注意:1)建立目标函数;2)求最值;(4)曲线的凹凸与拐点定义 定理1 方法1:方法2: 利用函数特性描绘函数图形.第一步第二步(5)函数图形的描绘 第三步第四步确定函数图形的水平、铅直渐近线以及其他变化趋势;第五步 (6)弧微分曲率曲率圆曲率的计算公式 定义 例1解二、典型例题 这就验证了命题的正确性. 例2解 例3证由介值定理, 注意到由,有+,得 例4证 例5证 –,则有 例6解 若两曲线满足题设条件,必在该点处具有相同的一阶导数和二阶导数,于是有 解此方程组得故所求作抛物线的方程为曲率圆的方程为两曲线在点处的曲率圆的圆心为 例7解奇函数 列表如下: 极大值拐点极小值 作图 测验题 测验题答案 '