最新复习课6ppt课件PPT课件 49页

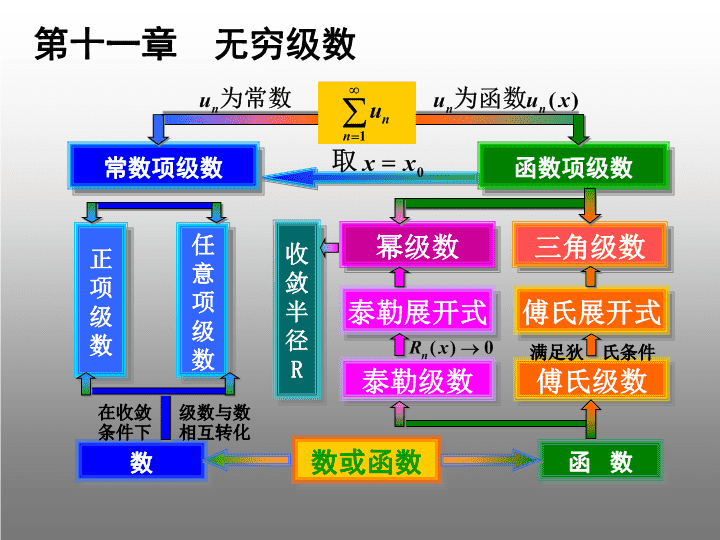
'复习课6ppt课件 常数项级数函数项级数正项级数幂级数三角级数收敛半径R泰勒展开式数或函数函数数任意项级数傅氏展开式傅氏级数泰勒级数满足狄氏条件在收敛级数与数条件下相互转化第十一章　无穷级数 设为上非负递减连续函数,那么级数与广义积分同时收敛或同时发散。 定义正、负项相间的级数称为交错级数.3、交错级数及其审敛法 定义正项和负项任意出现的级数称为任意项级数.4、任意项级数及其审敛法 5、函数项级数(1)定义(2)收敛点与收敛域 (3)和函数 (1)定义6、幂级数 (2)收敛性 推论 定义:正数R称为幂级数的收敛半径.幂级数的收敛域称为幂级数的收敛区间. a.代数运算性质:加减法(其中(3)幂级数的运算 乘法(其中除法 b.和函数的分析运算性质: 7、幂级数展开式(1)定义 (2)充要条件(3)唯一性 (3)展开方法a.直接法(泰勒级数法)步骤:b.间接法根据唯一性,利用常见展开式,通过变量代换,四则运算,恒等变形,逐项求导,逐项积分等方法,求展开式. (4)常见函数展开式 (5)应用a.近似计算b.欧拉公式 练习1.判定下列级数的敛散性 解 解(2) 解两边逐项积分 解４. 三、典型例题例解 根据级数收敛的必要条件，原级数发散． 解根据比较判别法，原级数收敛． 解从而有 原级数收敛；原级数发散；原级数也发散． 例解 例解即原级数非绝对收敛． 由莱布尼茨定理： 所以此交错级数收敛，故原级数是条件收敛． 例解 结束语谢谢大家聆听！！！49'