结构动力计算教学课件PPT 32页

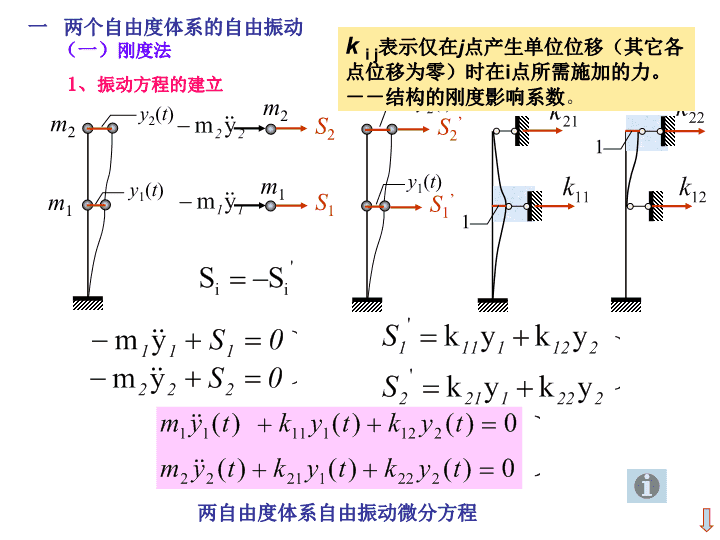
'第12章结构的动力计算第5讲 §12-6多自由度体系的自由振动两个自由度体系的自由振动二多自由度体系的自由振动 1、振动方程的建立两个自由度体系的自由振动（一）刚度法m1m2y1(t)y2(t)m1m2S2S1S2’S1’y1(t)y2(t)11两自由度体系自由振动微分方程kij表示仅在j点产生单位位移（其它各点位移为零）时在i点所需施加的力。－－结构的刚度影响系数。 设解为当然X(1)=X(2)=0为其解，为了求得不全为零的解，令特征方程频率方程1）在振动过程中，两个质点具有相同的频率和相同的相位角；2）在振动过程中，两个质点的位移在数值上随时间而变化，但其比值始终保持不变。*2频率的确定确定X(1)X(2)的方程 对应于这两个频率，可以分别得到两组解：最小圆频率称为第一(基本)圆频率：第二圆频率------- 3主振型（2）按主振型振动的条件：初位移或初速度与此振型相对应；m1m2X1(2)X1(1)X2(1)X2(2)由此可见：（1）多自由度体系如果按某个主振型自由振动，其振动形式保持不变，此时，多自由度体系实际上是像一个单自由度体系在振动(一个坐标即可表示所有质点位置）。实际上，多自由度体系在零时刻的y0或vo通常不能完全与某一振型相对应。振动过程中，结构位移形状保持不变的振动形式，称为主振型。第一主振型第二主振型 例1：设图示刚架横梁刚度为无限大，层间侧移刚度分别为k1和k2，试求刚架水平振动时的自由振动频率和主振型。m1m2k1k2解：（1）求频率方程中的刚度系数11k11=k1+k2k12=k21=-k2k22=k2（3）一般振动两自由度体系作一般自由振动是两种频率及其主振型的线性组合多自由度体系自由振动的振型分解11 （3）求主振型1.6181.01.00.618第1振型第2振型（2）求频率k11=k1+k2k12=k21=-k2k22=k2代频率方程若有 （3）求主振型若有若n=90则第一振型和第二振型分别为：可见当顶端质点的质量和刚度很小时，顶端水平侧移很大。建筑结构抗震设计中，将这种因顶端质点质量和刚度突变，而导致顶端巨大反应的现象，称为鞭梢效应。如：屋顶消防水池、女儿墙或屋顶建筑物等。 2、柔度法m1m2y1(t)y2(t)此时惯性力惯性力幅值主振型的位移幅值等于主振型惯性力幅值作用下产生的静力位移。m1m2δ11δ21=1m1m2δ12δ22=1在自由振动过程中任意时刻t，质量m1、m2的位移y1(t)、y2(t)应当等于体系在当时惯性力作用下的静力位移。设解为j点受单位力作用时i点产生的位移－－－柔度影响系数 m1m2X1X2令主振型频率方程**当然解X1=X2=0，为了求得不全为零的解，令 例2.求图示体系的频率、振型解则有：依据公式可求：** 1111第一振型第二振型对称体系的振型分成两组:一组为对称振型一组为反对称振型 0.5a例3.试求图示梁的自振频率和主振型，梁的EI已知。12aaamm解：（1）计算频率1a1（2）振型10.27713.61第一振型第二振型 二多个自由度体系的自由振动1运动方程的建立于是：写为矩阵形式：n自由度体系作无阻尼自由振动的运动微分方程 其中：对角矩阵，若一个质点上由两个位移yiyi+1则质量矩阵中第i及第i+1个相应位置元素均为mi对称方阵，主对角线上元素均为正值 2频率及主振型设运动方程具有特解：其中：体系按某一频率ω振动时n个质点的振幅列阵带入运动方程并整理后：若上述方程有非零解，则系数行列式为零：n个自由度体系的频率方程n个频率（按数值大小从小到大排列）：ω1，ω2，---，ωnn个自由度体系的振幅方程带入振型方程，可得：令：表示与频率ωj相对应的主振型向量：依上式可求得与ωj相对应主振型，我们可唯一地确定主振型的形状，但不能唯一地确定它的振幅。n个自由度体系的振型方程N自由度体系有n个主振型，若体系为对称形式，则这些主振型分为对称及反对称形式两类。 主振型的规准化：为了使主振型的振幅也具有确定值，需另外补充条件，由此得到的主振型叫规准化主振型。规准化方法1：规定主振型中某个元素为某个给定值，如，规定第一个元素Φj(1)为1，或最大的元素其值为1。规准化主振型向量用表示规准化方法2：规定主振型满足下式：两边同乘，得：n个自由度体系的规准化主振型方程 3柔度法运动方程的建立及频率、主振型的确定柔度矩阵n自由度体系作自由振动的运动方程（柔度法）将特解带入方程整理后：频率方程 规准化主振型方程一般的：阵型矩阵振型矩阵中每一列对应一个主振型（相应自己的频率）n个主振型向量彼此线性无关，阵型矩阵是满秩的，即是可逆的（非奇异的），阵型矩阵所对应的行列式不为零。 k22=k2例1：设图示刚架横梁刚度为无限大，层间侧移刚度分别为k1和k2，试求刚架水平振动时的自振动频率和主振型。m1m2k1k2（1）求频率方程中的刚度系数，确定刚度矩阵11k11=k1+k2k12=k21=-k2解：（一）求频率 （2）列频率方程，求出频率带入频率方程若有 （二）求主振型0.6181.6181.01.0第1振型第2振型求第一规准化阵型，将ω1带入上式同理可求： 3213211.5m1.5mm3211.5m1.5mm321例.计算图示体系的自振频率及主振型.1.5m1.5mm321解:令 由频率方程解得：即。分别代入振幅方程，可解出主振型向量，在规准化主振型中，规定第一个元素为1。取ω1：可解： 同理可得第二、第三主振型321321321 12.7多自由度体系主振型的正交性一.振型正交性由振型方程即：i振型、j振型分别有对上两式分别左乘第j、i振型的转置 对（11）式两边转置（111）-（22）因此：相对于质量矩阵来说，不同频率响应的主振型是彼此正交的由（22）式有：相对于刚度矩阵来说，不同频率响应的主振型是彼此正交的 振型对质量的正交性的物理意义j振型上的惯性力在i振型上作的虚功等于0，能量不会转移到其它振型上，各振型可以单独出现。对于规准化振型，正交性同样成立： 振型正交性的应用1.检验求解出的振型的正确性。例:试验证振型的正确性2.对耦联运动微分方程组作解耦运算等等. 例:已知图示体系的第一振型,试求第二振型.解: 11'