等腰三角形的性质课件PPT 25页

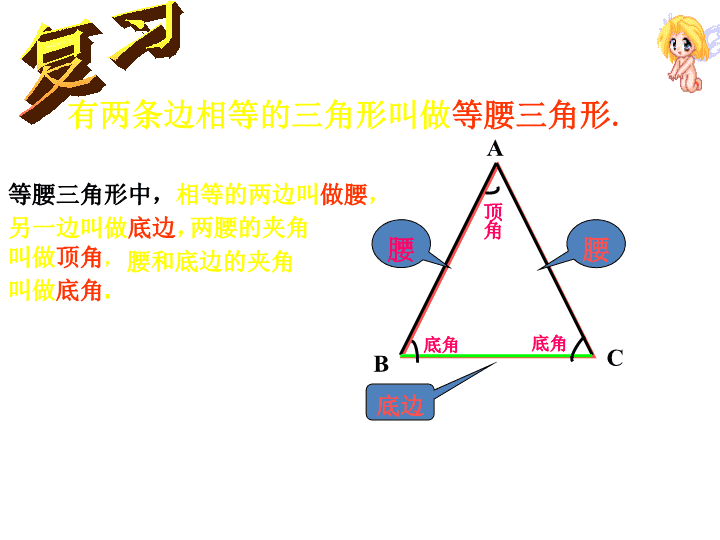
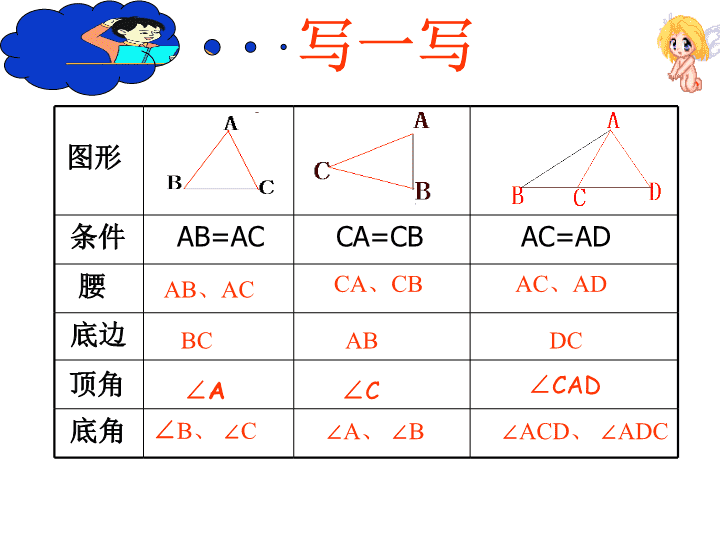
'八年级上数学12.3等腰三角形东升一中执教者：李卫华 有两条边相等的三角形叫做等腰三角形.等腰三角形中，相等的两边叫做腰，ACB腰腰底边顶角底角底角复习另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角. 条件AB=ACCA=CBAC=AD腰底边底角AB、ACBC∠B、∠CCA、CBAB∠A、∠BAC、AD∠ACD、∠ADCDC图形顶角∠A∠C∠CAD写一写 探究活动1、动手操作：把一张长方形纸片按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC有什么特点？2、想一想：（1）剪出的三角形是等腰三角形吗？并指出其中的腰、底边、顶角、底角。（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？（3）由这些重合的部分，你能发现等腰三角形的性质吗？说一说你的猜想。ABCD 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 动画演示AC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？腰腰底角ABCD 你发现了什么？结论1：等腰三角形的两底角相等ABC结论2：等腰三角形顶角的角平分线，既是底边上的中线，也是底边上的高。 探知求证：性质1、等腰三角形的两个底角相等。（等边对等角）ABCD已知：△ABC中，AB＝AC证明：作底边BC上的中线AD。在△ABD与△ACD中：AB＝AC（已知）BD＝DC（作图）AD＝AD（公共边）∴△ABD≌△ACD（SSS）∴∠B＝∠C（全等三角形对应角相等）ABC性质1用数学语言表示为：∵在△ABC中AB＝AC（已知）∴∠B＝∠C（等边对等角）求证：∠B＝∠C。 证法欣赏方法一：作顶角∠BAC的平分线AD。∵AD平分∠BAC∴∠1＝∠2在△ABD与△ACD中AB＝AC（已知）∠1＝∠2（已证）AD＝AD（公共边）∴△ABD≌△ACD（SAS）∴∠B＝∠CACB`D方法二：作底边BC的高AD。∵AD⊥BC∴∠ADB＝∠ADC＝90°在RT△ABD与RT△ACD中AB＝AC（已知）AD＝AD（公共边）∴△ABD≌△ACD（HL）∴∠B＝∠C112ABCD议一议:说说为什么在添加辅助线时，作顶角平分线，底边中线，底边高都能使分成的两个三角形全等？ 性质2：等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合。（通常说成等腰三角形的“三线合一”）性质2可分解成下面三个方面来理解：1、等腰三角形的顶角的平分线，既是底边上的中线，又是底边上的高。2、等腰三角形的底边上中线，既是底边上的高，又是顶角平分线。3、等腰三角形的底边上的高，既是底边上的中线，又是顶角平分线。ABCD21数学语言表示为：在△ABC中∵AB＝AC∠1＝∠2（已知）∴BD＝DCAD⊥BC（等腰三角形三线合一）数学语言表示为：在△ABC中∵AB＝ACBD＝DC（已知）∴AD⊥BC∠1＝∠2（等腰三角形三线合一）数学语言表示为：在△ABC中∵AB＝ACAD⊥BC（已知）∴BD＝DC∠1＝∠2（等腰三角形三线合一） 巩固练习1、练一练（基础训练）。（1）已知等腰三形的一个顶角为36°，则它的两个底角分别为。（2）已知等腰三角形的一个角为40°，则其它两个角分别为__。（3）已知等腰三角形的两边长分别是4和6，则它的周长是___________。72°、72°70°、70°40°、100°14或16（3题的变式题）若把此等腰三角形的两边长改为3和7，则它的周长应是多少？或 △ABC、△ADB、△DBC336°、72°、72°②△ABC的三个内角分别为_______________。ACBD（4）△ABC中，AB＝AC，D在AC上，且BD＝BC＝AD。①图中有个等腰三角形，它们分别为_______________。2X2XXX 能力训练△ABC中，AB＝AC，D是BC边上的中点，DF⊥AC于FDE⊥AB于E.求证：DE＝DF。ABCDEF证明：∵DE⊥AB，DF⊥AC（已知）∴∠BED＝∠CFD又∵D是BC中点（已知）∴BD＝DC∵AB＝AC（已知）∴∠B＝∠C（等边对等角）在△DBE与△DCF中∠DEB＝∠DFC（已证）∠B＝∠C（已证）BD＝DC（已证）∴△BDE≌△CDF（AAS）∴DE＝DF方法二：连AD。∵AB＝AC，BD＝DC（已知）∴AD是∠BAC的平分线。（等腰三角形三线合一）又∵DE⊥ABDF⊥AC∴DE＝DF（角平分线上的点到这个角的两边距离相等） 小结：通过本节课的学习你有收获吗？1、本节课的主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的两个底角相等等腰三角形的顶角平分线、底边上的中线底边上的高互相重合。∵AB＝AC（已知）∴∠B＝∠C（等边对等角）①∵AB＝AC，∠1＝∠2（已知）∴BD＝DC，AD⊥BC（三线合一）②∵AB＝AC，BD＝DC（已知）∴∠1＝∠2，AD⊥BC（三线合一）③∵AB＝AC，AD⊥BC（已知）∴∠1＝∠2，BD＝DC（三线合一）D122、本节课学习了数学思想及方法:分类讨论和一题多解。 布置作业1、P77练习1、2、3 '