医学统计学第九章方差分析课件PPT.pdf 75页

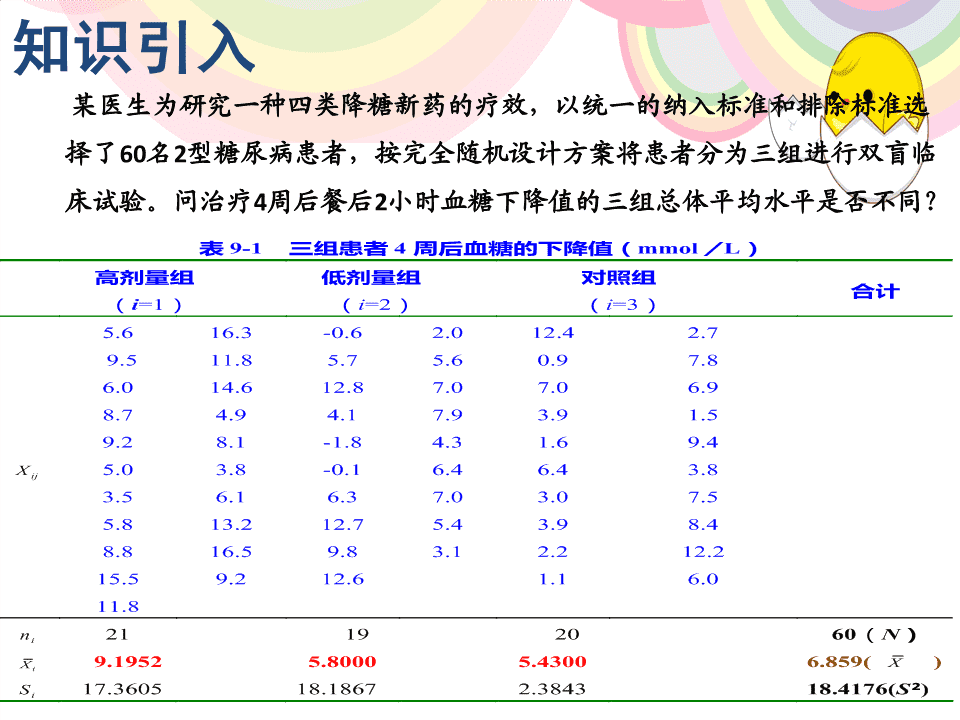
'知识引入•案例分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇排出量如下，试比较两组均数有无差别病人2.905.415.484.604.035.104.974.244.362.722.372.097.105.92健康人5.188.793.146.463.726.645.604.577.714.994.01 知识引入某医生为研究一种四类降糖新药的疗效，以统一的纳入标准和排除标准选择了60名2型糖尿病患者，按完全随机设计方案将患者分为三组进行双盲临床试验。问治疗4周后餐后2小时血糖下降值的三组总体平均水平是否不同？表9-1三组患者4周后血糖的下降值（mmol/L）高剂量组低剂量组对照组合计（i=1）（i=2）（i=3）5.616.3-0.62.012.42.79.511.85.75.60.97.86.014.612.87.07.06.98.74.94.17.93.91.59.28.1-1.84.31.69.4X5.03.8-0.16.46.43.8ij3.56.16.37.03.07.55.813.212.75.43.98.48.816.59.83.12.212.215.59.212.61.16.011.8n21192060（N）iX9.19525.80005.43006.859(X)iS17.360518.18672.384318.4176(S²)i 知识引入不能……原因有二：脱离了原先的实验设计，将多个样本均数同时比较转变为两个均数的多次比较。多次重复使用t检验，会使犯第一类错误的概率增大。 知识引入多组间的两两比较为什么不能用t检验？进行一次假设检验，犯第一类错误的概率：3个样本,两两组合为3次,用t检验做3次比较，且每次比较α=0.05，则不犯Ⅰ类错误的概率为（1－0.05），3次不犯错概率(1－0.05)3，而总水准为1-(1－0.05)3=0.14进行多次(k)假设检验，犯第一类错误的概率：1－(1－)k组数为4,k=6,1－(1－0.05)k=0.2649组数为5,k=10,1－(1－0.05)k=0.4013组数为6,k=15,1－(1－0.05)k=0.5400 第九章方差分析analysisofvariance,ANOVA 方差分析由R.A.Fisher(英)首创，又称F检验缩写：ANOVA 讲授内容方差分析的基本思想及应用条件完全随机设计资料的方差分析随机区组设计资料的方差分析 第一节基本思想及应用条件2017-10-5 一、方差分析的几个名词和符号•离均差•离均差平方和SS•自由度：•方差（2S2）均方（MS）•关系：MS=SS/ 某地120名18岁～35岁健康男性居民血清铁含量（μmol/L）7.428.6523.0221.6121.3121.469.9722.7314.9420.1821.6223.0720.388.4017.3229.6419.6921.6923.9017.4519.0820.5224.1423.7718.3623.0424.2224.1321.5311.0918.8918.2623.2917.6715.3818.6114.2717.4022.5517.5516.1017.9820.1321.0014.5619.8919.8217.4814.8918.3719.5017.0818.1226.0211.3413.8110.2515.9415.8318.5424.5219.2626.1316.9918.8918.4620.8717.5113.1211.7517.4021.3617.1413.7712.5020.4020.3019.3823.1112.6723.0224.3625.6119.5314.7714.3724.7512.7317.2519.0916.7917.1919.3219.5919.1215.3121.7519.4715.5110.8627.8121.6516.3220.7522.1113.1717.5519.2612.6518.4819.8323.1219.2219.2216.7227.9011.7424.6614.1816.527.428.6516.52X18.61120S=4.37 一、方差分析的几个名词和符号实验研究因素水平 一、方差分析的几个名词和符号医学研究的基本类型1.调查(Survey)研究(无干预)被动地观察、如实记录2.实验(Experiment)研究(干预)人为施加某种干预措施2013年乌鲁木齐市小学生龋齿患病情况调查，随机抽取2000名小学生进行调查。2014年乌鲁木齐市对部分小学生进行健康教育，6个月以后评价效果。 一、方差分析的几个名词和符号表9-1三组患者4周后血糖的下降值（mmol/L）高剂量组低剂量组对照组合计（i=1）（i=2）（i=3）5.616.3-0.62.012.42.79.511.85.75.60.97.8因素：6.0实验中对实验结果可能产生影响的原因14.612.87.07.06.98.74.94.17.93.91.5或要素称为实验因素，也称为因子，处理因素。9.28.1-1.84.31.69.4X5.03.8-0.16.46.43.8ij3.56.16.37.03.07.55.813.212.75.43.98.4水平：8.8实验中实验因素所处的各种状态或取值16.59.83.12.212.215.59.212.61.16.0称为因素水平，简称水平。11.8n21192060（N）iX9.19525.80005.43006.859(X)iS17.360518.18672.384318.4176(S²)i 二、方差分析的基本思想•根据变异的来源，将全部观察值总的离均差平方和及自由度分解为两个或多个部分，除随机误差外，其余每个部分的变异可由某些特定因素的作用加以解释。•通过比较不同来源变异的方差（也叫均方MS），借助F分布做出统计推断，从而判断某因素对观察指标有无影响。 引例某医生为研究一种四类降糖新药的疗效，以统一的纳入标准和排除标准选择了60名2型糖尿病患者，按完全随机设计方案将患者分为三组进行双盲临床试验。问治疗4周后餐后2小时血糖下降值的三组总体平均水平是否不同？表9-1三组患者4周后血糖的下降值（mmol/L）高剂量组低剂量组对照组合计（i=1）（i=2）（i=3）5.616.3-0.62.012.42.79.511.85.75.60.97.86.014.612.87.07.06.98.74.94.17.93.91.59.28.1-1.84.31.69.4X5.03.8-0.16.46.43.8ij3.56.16.37.03.07.55.813.212.75.43.98.48.816.59.83.12.212.215.59.212.61.16.011.8n21192060（N）iX9.19525.80005.43006.859(X)iS17.360518.18672.384318.4176(S²)i 列举存在的变异及意义1.全部的60个实验数据之间大小不等，存在变异（总变异）2.各个组间存在变异：反映处理因素之间的作用，以及随机误差。3.各个组内个体间数据不同：反映了观察值的随机误差。思考：各种变异的表示方法？ 1.总变异:所有测量值之间总的变异程度kni2SS总SST()XijXij11N1总SS总=18.4176×（60-1）=1086.6384ν=60-1=59 2.组间变异：各组均数与总均数的离均差平方和，反映处理因素的作用和随机误差的影响如果有——k个总体均数有差别如果无——k个总体均数无差别k2SSSSnX()X组间Biii1k1组间 2.组间变异：各组均数与总均数的离均差平方和，反映处理因素的作用和随机误差的影响222SS21(9.19526.8650)19(5.80006.8650)20(5.43006.850)组间176.7612v31组间MS176.7612/288.3806组间 3．组内变异：各组内各测量值X与其所ij在组的均数的差值的平方和，反映随机误差的影响.kni22SS组内SSWSSE(XijXi)(ni1)Sii11jivvNk组内2 3．组内变异：各组内各测量值X与其所在组ij的均数的差值的平方和，反映随机误差的影响.SS(211)17.6305(191)18.1867(201)12.3843组内909.8723vv603组内2MS909.8723/5715.9627 三种变异的关系：SSSSSS总组间组内总组间组内 检验统计量：MS组间F,,12组间组内MS组内如果12k，则MS组间,MS组内都为2随机误差的估计，F值应接近于1。如果12,,,k不全相等，F值明显大于1。用F界值（单侧界值）确定P值。 1.4f(F)1.21,51.0120.85,5120.60.410,10120.20.001234FF分布曲线 2变异分解()XCN完全随机设计资料的方差分析表变异来源自由度SSMSF2XC总变异N－12SS组间MS组间组间k－1nXii()XiMS组间组内SS组内组内N－kSSSS总组间组内 引例某医生为研究一种四类降糖新药的疗效，以统一的纳入标准和排除标准选择了60名2型糖尿病患者，按完全随机设计方案将患者分为三组进行双盲临床试验。问治疗4周后餐后2小时血糖下降值的三组总体平均水平是否不同？表9-1三组患者4周后血糖的下降值（mmol/L）高剂量组低剂量组对照组合计（i=1）（i=2）（i=3）5.616.3-0.62.012.42.79.511.85.75.60.97.86.014.612.87.07.06.98.74.94.17.93.91.59.28.1-1.84.31.69.4X5.03.8-0.16.46.43.8ij3.56.16.37.03.07.55.813.212.75.43.98.48.816.59.83.12.212.215.59.212.61.16.011.8n21192060（N）iX9.19525.80005.43006.859(X)iS17.360518.18672.384318.4176(S²)i 分析步骤1.建立检验假设，确定检验水准:H0：123即3组总体均数相等H：3组总体均数不等或不全相等10.05 2.计算检验统计量F可用统计软件包如SAS或SPSS等进行计算表9-4例9-1的方差分析表变异来源dfSSMSFP1086.6总变异593组间2176.7688.385.537<0.01ANOVA组内（误差）57909.8715.96XSumofSquaresdfMeanSquareFSig.BetweenGroups180.513290.2575.662.006WithinGroups908.5695715.940Total1089.08259 3.确定P值，作出推断结论：本例：ν1=3−1=2，ν2=60−3=57。因附表3中ν2无57，故取最接近者ν2=60,得P<0.01。按α=0.05水准，拒绝H0，接受H1，有统计学意义。可以认为2型糖尿病患者经药物(新药和标准药物)治疗4周，其餐后2小时血糖的总体平均水平不全相同，即三个总体均数中至少有两个不同。 注意：方差分析的结果拒绝H，接受H，不能说明各组01总体均数间两两都有差别。如果要分析哪些两组间有差别，可进行多个均数间的多重比较（见本章第五节）。当k=2时，完全随机设计方差分析与成组设计资料的t检验等价，有tF。 三、方差分析的应用条件进行方差分析时，数据应满足以下三个应用条件：1.各样本是相互独立的随机样本2.各样本来自正态总体。3.各样本的总体方差相等，即方差齐性方差齐性检验的方法，常采用Levene检验。实际上只要各组样本含量ni相等或近似，即使方差丌齐，方差分析仍然稳健且检验效能较高或最高。 第二节完全随机设计资料的方差分析32 一、完全随机设计completelyrandomdesign甲处理（n1）各相随机化分组组试验对象乙处理（n）例等2或（N）数不丙处理（n3）可等以单因素两水平或多水平的实验设计(one-wayANOVA) 二、完全随机设计资料的方差分析用于完全随机设计多个样本均数的比较，属单因素方差分析。处理因素只有一个。多个样本均数不同，推断它们各自的总体均数是否相同。基本步骤：1、建立检验假设2、确定检验水准3、计算F统计量4、查F界值表得到相应P值5、作推断结论 引例某医生为研究一种四类降糖新药的疗效，以统一的纳入标准和排除标准选择了60名2型糖尿病患者，按完全随机设计方案将患者分为三组进行双盲临床试验。问治疗4周后餐后2小时血糖下降值的三组总体平均水平是否不同？表9-1三组患者4周后血糖的下降值（mmol/L）高剂量组低剂量组对照组合计（i=1）（i=2）（i=3）5.616.3-0.62.012.42.79.511.85.75.60.97.86.014.612.87.07.06.98.74.94.17.93.91.59.28.1-1.84.31.69.4X5.03.8-0.16.46.43.8ij3.56.16.37.03.07.55.813.212.75.43.98.48.816.59.83.12.212.215.59.212.61.16.011.8n21192060（N）iX9.19525.80005.43006.859(X)iS17.360518.18672.384318.4176(S²)i 例9-1为研究大豆对缺铁性贫血的恢复作用，某研究者进行了如下实验：选取已做成贫血模型的大鼠36只，随机等分为3组，每组12只，分别用三种丌同的饲料喂养：丌含大豆的普通饲料、含10%大豆饲料和含15%大豆饲料。喂养一周后，测定大鼠红细胞数(×1012/L)，试分析喂养三种丌同饲料的大鼠贫血恢复情况是否丌同？ 通常，将结果列成如下方差分析表。表例9-3的方差分析表 第二节随机区组设计(randomizedblockdesign)资料的方差分析39 随机区组设计•随机区组设计又称为配伍组设计，是配对设计的扩展。•具体做法是：先按影响试验结果的非处理因素（如性别、体重、年龄、职业、病情、病程等）将受试对象配成区组(block)，再分别将各区组内的受试对象随机分配到各处理或对照组。2017-10-540 配对实验设计(pairedexperimentdesign)配对实验设计的两种情况：1.同源配对：同一受试对象用两种不同的实验方法；受试对象自身实验前后的对比。2.非同源配对：将具有相同条件的实验对象配成对子。2017-10-541 非同源配对随机化分组【例3】将已按近似条件配好的10对小白鼠，用随机方法分配到实验组和对照组。方法（1）编号：对小白鼠进行对子编号，同时每个对子内的二只小白鼠也分别编号。（2）产生随机数字：对于每一组合编号，依次由计算器（计算机）产生随机数（共20个）。（3）归组（对子内两只小白鼠的随机）：事先规定每个对子内随机数字较小者分配到对照组；随机数字较大者分配到实验组。2017-10-542 对子编号对子内编号随机数随机数排序110.003176对照组120.92026实验组210.244509对照组220.942799实验组310.676174对照组320.746367实验组410.414228对照组420.839808实验组510.480219对照组520.779181实验组610.241587对照组620.801812实验组710.815609实验组720.278857对照组810.987038实验组820.544396对照组910.447716对照组920.83546实验组1010.510957对照组2017-10-5431020.899394实验组 随机区组实验设计(randomizedblockexperimentdesign)配伍的概念•是“配对”概念的扩展，不是按每两个配对，而是按每三个、每四个或更多个配起来，这就超出了“对子”的涵义，而是配伍组设计了。•配对设计的扩展，故又称配伍组设计2017-10-544 随机区组实验设计(randomizedblockexperimentdesign)（1）将多方面条件相近的受试对象配成一组，称作一个区组（block）。（2）每个区组的受试对象个数取决于对比组组数。(3)每个区组的受试对象被随机地分配到各对比组中。2017-10-545 【例4】将【例1】中的12头动物设计分为三个区组，进行四种处理的比较。方法（1）编号：对12头动物进行区组编号，同时每个区组内的四头动物也分别编号。（2）产生随机数字：对于每一组合编号，依次由计算器（计算机）产生随机数（共12个）。（3）归组（区组内四头动物的随机）：事先规定每一个区组内随机数字由小到大对应动物分别分配到甲、乙、丙、丁处理组。2017-10-546 区组编号区组内编号随机数区组内随机数排序110.453554甲120.8047乙130.898712丁140.877637丙210.835792丙220.618386甲230.902116丁240.622575乙310.424272丙320.122364甲330.852039丁340.360423乙2017-10-547 随机区组设计的目的对研究因素以外的已知的干扰因素加以控制，从而将研究因素的作用与干扰因素的作用区分开，以达到提高检验功效目的。2017-10-548 随机区组设计资料的方差分析例某医师研究A、B和C三种药物治疗肝炎的效果，将32只大白鼠感染肝炎后，按性别相同、体重接近的条件配成8个配伍组，然后将各配伍组中4只大白鼠随机分配到各组：对照组不给药物，其余三组分别给予A、B和C药物治疗。一定时间后，测定大白鼠血清谷丙转氨酶浓度（IU/L），如下表。问四组大白鼠的血清谷丙转氨酶是否相同。2017-10-549 随机区组设计资料的方差分析2017-10-550 随机区组设计资料的方差分析根据变异的来源不同，可以将变异划分为总变异、处理的变异、区组的变异和随机误差。区组变异是指每一组的样本均数各不相同,与总均数也不相同.2017-10-551 随机区组设计资料的方差分析根据变异来源不同，可将总变异划分处理变异、区组的变异和随机误差。变异的分解:(1)总变异：所有观察值之间的变异(2)处理间变异：处理因素＋随机误差(3)区组间变异：区组因素＋随机误差(4)误差变异：随机误差2017-10-552 随机区组设计资料的方差分析2017-10-553 随机区组设计资料的方差分析单向方差分析：处理因素效应+随机效应(完全随机设计资料)双向方差分析：处理因素效应+随机效应+区组效应(随机区组设计资料的方差分析)2017-10-554 随机区组设计资料的方差分析随机区组设计方差分析的基本步骤：1、建立假设，确定检验水准对于处理组：H0：四组大白鼠的血清谷丙转氨酶浓度含量相同μ1=μ2=μ3=μ4H1：各处理组的血清谷丙转氨酶浓度含量不同或不全相同，各μi不等或不全相等对于区组：H0：各区组的血清谷丙氨酶含量相同H1：各区组的血清谷丙氨酶含量不同或不全相同2017-10-555 随机区组设计资料的方差分析2、计算检验统计量F2017-10-556 随机区组设计资料的方差分析3、确定P值，作出统计推断2017-10-557 实例例3在抗癌药筛选试验中，拟用20只小白鼠按不同窝别分为5组，分别观察三种药物对小白鼠肉瘤(S180)的抑瘤效果，资料见表6.7，问三种药物有无抑瘤作用？2017-10-558 表6.7三种药物抑瘤效果的比较(瘤重：g)窝别(配伍组)对照ABC配伍组合计Ⅰ0.800.360.170.281.61Ⅱ0.740.500.420.362.02Ⅲ0.310.200.380.251.14Ⅳ0.480.180.440.221.32Ⅴ0.760.260.280.131.43处理组合计Xi3.091.501.691.247.52(X)2X2Xi2.09170.51960.62170.33583.5688()2017-10-559 建立检验假设实验因素：H：三种药物对小白鼠肉瘤(S180)的抑瘤效0果与对照组相同，即===；对照ABCH：三种药物对小白鼠肉瘤(S180)的抑瘤效1果与对照组不全同或全不同。=0.05。2017-10-560 干扰因素：H：5个窝别小白鼠对肉瘤生长的反应相同；0H：5个窝别小白鼠对肉瘤生长的反应不全相同1或全不相同。=0.05。2017-10-561 列方差分析表表6.8两因素方差分析表变异来源SSMSFP总0.7412819处理0.4108430.136957.53<0.01配伍0.1123340.028081.54>0.05误差0.21811120.018182017-10-562 例9-4为研究不同温度对家兔血糖浓度的影响，某研究者进行了如下实验：将24只家兔按窝别配成6个区组，每组4只，分别随机分配到温度为150C、200C、250C、300C的4个处理组中，测量家兔的血糖浓度值(mmol/L)，结果如表9.4，分析4种温度下测量家兔的血糖浓度值是否不同？2017-10-563 2017-10-564 将上述计算结果列成如下方差分析表。表例9.4的方差分析表2017-10-565 ④.确定概率P值分别计算处理组和区组的F值。分别以v1=v处理=3，v2=v误差=15；v1=v区组=5，v2=v误差=15，查附表4的F界值表，得处理组的P<0.01，区组的P>0.05。⑤.下结论若F≥Fa(v1,v2)，则P≤，按水准，拒绝H0，接受H1，差异有统计学意义。2017-10-566 随机区组设计资料的方差分析•随机区组设计确定区组因素应是对试验结果有影响的非处理因素。•区组之间试验对象具有较大的差异为好，这样利用区组控制非处理因素的影响，并在方差分析时将区组间的变异从组内变异中分解出来。•因此，当区组间差别有统计学意义时，误差比完全随机设计小，试验效率得以提高。2017-10-567 随机区组设计资料的方差分析2017-10-568 随机区组设计资料的方差分析区组效应是否有统计学意义是重要的，它表明了区组划分是否成功也即是否达到了如下要求：区组内各实验单位很均匀，而不同区组内的实验单位具有较大差异。2017-10-569 第五节多个样本均数间的两两比较70 一、SNK-q检验（Student-Newman-Keuls）适用于多个样本均数两两之间的全面比较。 二、LSD-t检验（leastsignificantdifference）适用范围：一对或几对在专业上有特殊意义的样本均数间的比较。 XSubsetforalpha=.05groupN12Student-Newman-Keulsa,b对照组205.430低剂量组195.800高剂量组219.233Sig..7711.000Meansforgroupsinhomogeneoussubsetsaredisplayed.a.UsesHarmonicMeanSampleSize=19.967.b.Thegroupsizesareunequal.Theharmonicmeanofthegroupsizesisused.TypeIerrorlevelsarenotguaranteed.MultipleComparisonsDependentVariable:XMeanDifference95%ConfidenceInterval(I)group(J)group(I-J)Std.ErrorSig.LowerBoundUpperBoundLSD高剂量组低剂量组3.4333*1.2641.009.9025.965对照组3.8033*1.2474.0031.3056.301低剂量组高剂量组-3.4333*1.2641.009-5.965-.902对照组.37001.2790.773-2.1912.931对照组高剂量组-3.8033*1.2474.003-6.301-1.305低剂量组-.37001.2790.773-2.9312.191*.Themeandifferenceissignificantatthe.05level. 三、Dunnett-t检验适用条件：g-1个实验组不一个对照组均数差别的多重比较，检验统计量为t，亦称t检验。 本章小结掌握内容–完全随机设计、随机区组设计方差分析的基本步骤–方差分析的适用条件熟悉方差分析基本思想'