数据库系统概念全套配套课件PPT ch8.ppt 92页

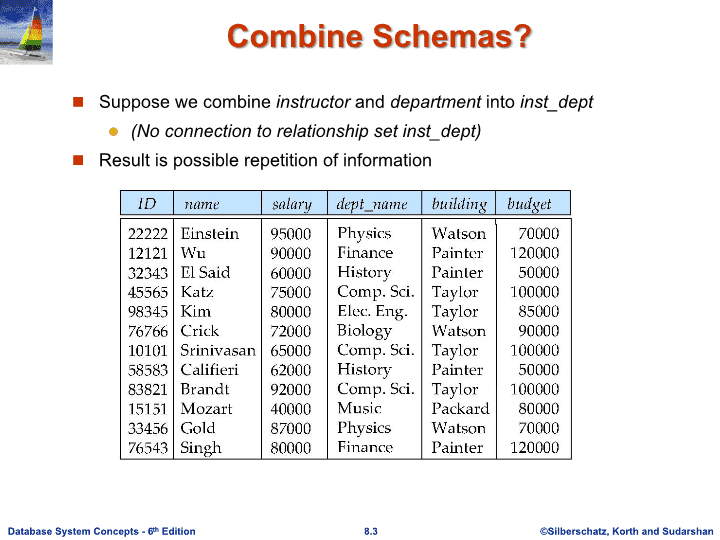
'Chapter8:RelationalDatabaseDesign Chapter8:RelationalDatabaseDesignFeaturesofGoodRelationalDesignAtomicDomainsandFirstNormalFormDecompositionUsingFunctionalDependenciesFunctionalDependencyTheoryAlgorithmsforFunctionalDependenciesDecompositionUsingMultivaluedDependenciesMoreNormalFormDatabase-DesignProcessModelingTemporalData CombineSchemas?Supposewecombineinstructoranddepartmentintoinst_dept(Noconnectiontorelationshipsetinst_dept)Resultispossiblerepetitionofinformation ACombinedSchemaWithoutRepetitionConsidercombiningrelationssec_class(sec_id,building,room_number)andsection(course_id,sec_id,semester,year)intoonerelationsection(course_id,sec_id,semester,year,building,room_number)Norepetitioninthiscase WhatAboutSmallerSchemas?Supposewehadstartedwithinst_dept.Howwouldweknowtosplitup(decompose)itintoinstructoranddepartment?Writearule“iftherewereaschema(dept_name,building,budget),thendept_namewouldbeacandidatekey”Denoteasafunctionaldependency:dept_namebuilding,budgetIninst_dept,becausedept_nameisnotacandidatekey,thebuildingandbudgetofadepartmentmayhavetoberepeated.Thisindicatestheneedtodecomposeinst_deptNotalldecompositionsaregood.Supposewedecomposeemployee(ID,name,street,city,salary)intoemployee1(ID,name)employee2(name,street,city,salary)Thenextslideshowshowweloseinformation--wecannotreconstructtheoriginalemployeerelation--andso,thisisalossydecomposition. ALossyDecomposition ExampleofLossless-JoinDecompositionLosslessjoindecompositionDecompositionofR=(A,B,C)R1=(A,B)R2=(B,C)AB12AB12rB,C(r)A(r)B(r)AB12CABB12CABCABA,B(r) FirstNormalFormDomainisatomicifitselementsareconsideredtobeindivisibleunitsExamplesofnon-atomicdomains:Setofnames,compositeattributesIdentificationnumberslikeCS101thatcanbebrokenupintopartsArelationalschemaRisinfirstnormalformifthedomainsofallattributesofRareatomicNon-atomicvaluescomplicatestorageandencourageredundant(repeated)storageofdataExample:Setofaccountsstoredwitheachcustomer,andsetofownersstoredwitheachaccountWeassumeallrelationsareinfirstnormalform(andrevisitthisinChapter22:ObjectBasedDatabases) FirstNormalForm(Cont’d)Atomicityisactuallyapropertyofhowtheelementsofthedomainareused.Example:StringswouldnormallybeconsideredindivisibleSupposethatstudentsaregivenrollnumberswhicharestringsoftheformCS0012orEE1127Ifthefirsttwocharactersareextractedtofindthedepartment,thedomainofrollnumbersisnotatomic.Doingsoisabadidea:leadstoencodingofinformationinapplicationprogramratherthaninthedatabase. Goal—DeviseaTheoryfortheFollowingDecidewhetheraparticularrelationRisin“good”form.InthecasethatarelationRisnotin“good”form,decomposeitintoasetofrelations{R1,R2,...,Rn}suchthateachrelationisingoodformthedecompositionisalossless-joindecompositionOurtheoryisbasedon:functionaldependenciesmultivalueddependencies FunctionalDependenciesConstraintsonthesetoflegalrelations.Requirethatthevalueforacertainsetofattributesdeterminesuniquelythevalueforanothersetofattributes.Afunctionaldependencyisageneralizationofthenotionofakey. FunctionalDependencies(Cont.)LetRbearelationschemaRandRThefunctionaldependencyholdsonRifandonlyifforanylegalrelationsr(R),wheneveranytwotuplest1andt2ofragreeontheattributes,theyalsoagreeontheattributes.Thatis,t1[]=t2[]t1[]=t2[]Example:Considerr(A,B)withthefollowinginstanceofr.Onthisinstance,ABdoesNOThold,butBAdoeshold.41537 FunctionalDependencies(Cont.)KisasuperkeyforrelationschemaRifandonlyifKRKisacandidatekeyforRifandonlyifKR,andfornoK,RFunctionaldependenciesallowustoexpressconstraintsthatcannotbeexpressedusingsuperkeys.Considertheschema:inst_dept(ID,name,salary,dept_name,building,budget).Weexpectthesefunctionaldependenciestohold:dept_namebuildingandIDbuildingbutwouldnotexpectthefollowingtohold:dept_namesalary UseofFunctionalDependenciesWeusefunctionaldependenciesto:testrelationstoseeiftheyarelegalunderagivensetoffunctionaldependencies.IfarelationrislegalunderasetFoffunctionaldependencies,wesaythatrsatisfiesF.specifyconstraintsonthesetoflegalrelationsWesaythatFholdsonRifalllegalrelationsonRsatisfythesetoffunctionaldependenciesF.Note:Aspecificinstanceofarelationschemamaysatisfyafunctionaldependencyevenifthefunctionaldependencydoesnotholdonalllegalinstances.Forexample,aspecificinstanceofinstructormay,bychance,satisfynameID. FunctionalDependencies(Cont.)AfunctionaldependencyistrivialifitissatisfiedbyallinstancesofarelationExample:ID,nameIDnamenameIngeneral,istrivialif ClosureofaSetofFunctionalDependenciesGivenasetFoffunctionaldependencies,therearecertainotherfunctionaldependenciesthatarelogicallyimpliedbyF.Forexample:IfABandBC,thenwecaninferthatACThesetofallfunctionaldependencieslogicallyimpliedbyFistheclosureofF.WedenotetheclosureofFbyF+.F+isasupersetofF. Boyce-CoddNormalFormistrivial(i.e.,)isasuperkeyforRArelationschemaRisinBCNFwithrespecttoasetFoffunctionaldependenciesifforallfunctionaldependenciesinF+oftheformwhereRandR,atleastoneofthefollowingholds:ExampleschemanotinBCNF:instr_dept(ID,name,salary,dept_name,building,budget)becausedept_namebuilding,budgetholdsoninstr_dept,butdept_nameisnotasuperkey DecomposingaSchemaintoBCNFSupposewehaveaschemaRandanon-trivialdependencycausesaviolationofBCNF.WedecomposeRinto:(U)(R-(-))Inourexample,=dept_name=building,budgetandinst_deptisreplacedby(U)=(dept_name,building,budget)(R-(-))=(ID,name,salary,dept_name) BCNFandDependencyPreservationConstraints,includingfunctionaldependencies,arecostlytocheckinpracticeunlesstheypertaintoonlyonerelationIfitissufficienttotestonlythosedependenciesoneachindividualrelationofadecompositioninordertoensurethatallfunctionaldependencieshold,thenthatdecompositionisdependencypreserving.BecauseitisnotalwayspossibletoachievebothBCNFanddependencypreservation,weconsideraweakernormalform,knownasthirdnormalform. ThirdNormalFormArelationschemaRisinthirdnormalform(3NF)ifforall:inF+atleastoneofthefollowingholds:istrivial(i.e.,)isasuperkeyforREachattributeAin–iscontainedinacandidatekeyforR.(NOTE:eachattributemaybeinadifferentcandidatekey)IfarelationisinBCNFitisin3NF(sinceinBCNFoneofthefirsttwoconditionsabovemusthold).ThirdconditionisaminimalrelaxationofBCNFtoensuredependencypreservation(willseewhylater). GoalsofNormalizationLetRbearelationschemewithasetFoffunctionaldependencies.DecidewhetherarelationschemeRisin“good”form.InthecasethatarelationschemeRisnotin“good”form,decomposeitintoasetofrelationscheme{R1,R2,...,Rn}suchthateachrelationschemeisingoodformthedecompositionisalossless-joindecompositionPreferably,thedecompositionshouldbedependencypreserving. HowgoodisBCNF?TherearedatabaseschemasinBCNFthatdonotseemtobesufficientlynormalizedConsiderarelationinst_info(ID,child_name,phone)whereaninstructormayhavemorethanonephoneandcanhavemultiplechildrenIDchild_namephone99999999999999999999DavidDavidWilliamWillian512-555-1234512-555-4321512-555-1234512-555-4321inst_info Therearenonon-trivialfunctionaldependenciesandthereforetherelationisinBCNFInsertionanomalies–i.e.,ifweaddaphone981-992-3443to99999,weneedtoaddtwotuples(99999,David,981-992-3443)(99999,William,981-992-3443)HowgoodisBCNF?(Cont.) Therefore,itisbettertodecomposeinst_infointo:Thissuggeststheneedforhighernormalforms,suchasFourthNormalForm(4NF),whichweshallseelater.HowgoodisBCNF?(Cont.)IDchild_name99999999999999999999DavidDavidWilliamWillianinst_childIDphone99999999999999999999512-555-1234512-555-4321512-555-1234512-555-4321inst_phone Functional-DependencyTheoryWenowconsidertheformaltheorythattellsuswhichfunctionaldependenciesareimpliedlogicallybyagivensetoffunctionaldependencies.WethendevelopalgorithmstogeneratelosslessdecompositionsintoBCNFand3NFWethendevelopalgorithmstotestifadecompositionisdependency-preserving ClosureofaSetofFunctionalDependenciesGivenasetFsetoffunctionaldependencies,therearecertainotherfunctionaldependenciesthatarelogicallyimpliedbyF.Fore.g.:IfABandBC,thenwecaninferthatACThesetofallfunctionaldependencieslogicallyimpliedbyFistheclosureofF.WedenotetheclosureofFbyF+. ClosureofaSetofFunctionalDependenciesWecanfindF+,theclosureofF,byrepeatedlyapplyingArmstrong’sAxioms:if,then(reflexivity)if,then(augmentation)if,and,then(transitivity)Theserulesaresound(generateonlyfunctionaldependenciesthatactuallyhold),andcomplete(generateallfunctionaldependenciesthathold). ExampleR=(A,B,C,G,H,I)F={ABACCGHCGIBH}somemembersofF+AHbytransitivityfromABandBHAGIbyaugmentingACwithG,togetAGCGandthentransitivitywithCGICGHIbyaugmentingCGItoinferCGCGI,andaugmentingofCGHtoinferCGIHI,andthentransitivity ProcedureforComputingF+TocomputetheclosureofasetoffunctionaldependenciesF:F+=FrepeatforeachfunctionaldependencyfinF+applyreflexivityandaugmentationrulesonfaddtheresultingfunctionaldependenciestoF+foreachpairoffunctionaldependenciesf1andf2inF+iff1andf2canbecombinedusingtransitivitythenaddtheresultingfunctionaldependencytoF+untilF+doesnotchangeanyfurtherNOTE:Weshallseeanalternativeprocedureforthistasklater ClosureofFunctionalDependencies(Cont.)Additionalrules:Ifholdsandholds,thenholds(union)Ifholds,thenholdsandholds(decomposition)Ifholdsandholds,thenholds(pseudotransitivity)TheaboverulescanbeinferredfromArmstrong’saxioms. ClosureofAttributeSetsGivenasetofattributesa,definetheclosureofaunderF(denotedbya+)asthesetofattributesthatarefunctionallydeterminedbyaunderFAlgorithmtocomputea+,theclosureofaunderFresult:=a;while(changestoresult)doforeachinFdobeginifresultthenresult:=resultend ExampleofAttributeSetClosureR=(A,B,C,G,H,I)F={ABACCGHCGIBH}(AG)+1.result=AG2.result=ABCG(ACandAB)3.result=ABCGH(CGHandCGAGBC)4.result=ABCGHI(CGIandCGAGBCH)IsAGacandidatekey?IsAGasuperkey?DoesAGR?==Is(AG)+RIsanysubsetofAGasuperkey?DoesAR?==Is(A)+RDoesGR?==Is(G)+R UsesofAttributeClosureThereareseveralusesoftheattributeclosurealgorithm:Testingforsuperkey:Totestifisasuperkey,wecompute+,andcheckif+containsallattributesofR.TestingfunctionaldependenciesTocheckifafunctionaldependencyholds(or,inotherwords,isinF+),justcheckif+.Thatis,wecompute+byusingattributeclosure,andthencheckifitcontains.Isasimpleandcheaptest,andveryusefulComputingclosureofFForeachR,wefindtheclosure+,andforeachS+,weoutputafunctionaldependencyS. CanonicalCoverSetsoffunctionaldependenciesmayhaveredundantdependenciesthatcanbeinferredfromtheothersForexample:ACisredundantin:{AB,BC,AC}PartsofafunctionaldependencymayberedundantE.g.:onRHS:{AB,BC,ACD}canbesimplifiedto{AB,BC,AD}E.g.:onLHS:{AB,BC,ACD}canbesimplifiedto{AB,BC,AD}Intuitively,acanonicalcoverofFisa“minimal”setoffunctionaldependenciesequivalenttoF,havingnoredundantdependenciesorredundantpartsofdependencies ExtraneousAttributesConsiderasetFoffunctionaldependenciesandthefunctionaldependencyinF.AttributeAisextraneousinifAandFlogicallyimplies(F–{}){(–A)}.AttributeAisextraneousinifAandthesetoffunctionaldependencies(F–{}){(–A)}logicallyimpliesF.Note:implicationintheoppositedirectionistrivialineachofthecasesabove,sincea“stronger”functionaldependencyalwaysimpliesaweakeroneExample:GivenF={AC,ABC}BisextraneousinABCbecause{AC,ABC}logicallyimpliesAC(I.e.theresultofdroppingBfromABC).Example:GivenF={AC,ABCD}CisextraneousinABCDsinceABCcanbeinferredevenafterdeletingC TestingifanAttributeisExtraneousConsiderasetFoffunctionaldependenciesandthefunctionaldependencyinF.TotestifattributeAisextraneousincompute({}–A)+usingthedependenciesinFcheckthat({}–A)+contains;ifitdoes,AisextraneousinTotestifattributeAisextraneousincompute+usingonlythedependenciesinF’=(F–{}){(–A)},checkthat+containsA;ifitdoes,Aisextraneousin CanonicalCoverAcanonicalcoverforFisasetofdependenciesFcsuchthatFlogicallyimpliesalldependenciesinFc,andFclogicallyimpliesalldependenciesinF,andNofunctionaldependencyinFccontainsanextraneousattribute,andEachleftsideoffunctionaldependencyinFcisunique.TocomputeacanonicalcoverforF:repeatUsetheunionruletoreplaceanydependenciesinF11and12with112Findafunctionaldependencywithanextraneousattributeeitherinorin/*Note:testforextraneousattributesdoneusingFc,notF*/Ifanextraneousattributeisfound,deleteitfromuntilFdoesnotchangeNote:Unionrulemaybecomeapplicableaftersomeextraneousattributeshavebeendeleted,soithastobere-applied ComputingaCanonicalCoverR=(A,B,C)F={ABCBCABABC}CombineABCandABintoABCSetisnow{ABC,BC,ABC}AisextraneousinABCCheckiftheresultofdeletingAfromABCisimpliedbytheotherdependenciesYes:infact,BCisalreadypresent!Setisnow{ABC,BC}CisextraneousinABCCheckifACislogicallyimpliedbyABandtheotherdependenciesYes:usingtransitivityonABandBC.CanuseattributeclosureofAinmorecomplexcasesThecanonicalcoveris:ABBC Lossless-joinDecompositionForthecaseofR=(R1,R2),werequirethatforallpossiblerelationsronschemaRr=R1(r)R2(r)AdecompositionofRintoR1andR2islosslessjoinifatleastoneofthefollowingdependenciesisinF+:R1R2R1R1R2R2Theabovefunctionaldependenciesareasufficientconditionforlosslessjoindecomposition;thedependenciesareanecessaryconditiononlyifallconstraintsarefunctionaldependencies ExampleR=(A,B,C)F={AB,BC)CanbedecomposedintwodifferentwaysR1=(A,B),R2=(B,C)Lossless-joindecomposition:R1R2={B}andBBCDependencypreservingR1=(A,B),R2=(A,C)Lossless-joindecomposition:R1R2={A}andAABNotdependencypreserving(cannotcheckBCwithoutcomputingR1R2) DependencyPreservationLetFibethesetofdependenciesF+thatincludeonlyattributesinRi.Adecompositionisdependencypreserving,if(F1F2…Fn)+=F+Ifitisnot,thencheckingupdatesforviolationoffunctionaldependenciesmayrequirecomputingjoins,whichisexpensive. TestingforDependencyPreservationTocheckifadependencyispreservedinadecompositionofRintoR1,R2,…,Rnweapplythefollowingtest(withattributeclosuredonewithrespecttoF)result=while(changestoresult)doforeachRiinthedecompositiont=(resultRi)+Riresult=resulttIfresultcontainsallattributesin,thenthefunctionaldependencyispreserved.WeapplythetestonalldependenciesinFtocheckifadecompositionisdependencypreservingThisproceduretakespolynomialtime,insteadoftheexponentialtimerequiredtocomputeF+and(F1F2…Fn)+ ExampleR=(A,B,C)F={ABBC}Key={A}RisnotinBCNFDecompositionR1=(A,B),R2=(B,C)R1andR2inBCNFLossless-joindecompositionDependencypreserving TestingforBCNFTocheckifanon-trivialdependencycausesaviolationofBCNF1.compute+(theattributeclosureof),and2.verifythatitincludesallattributesofR,thatis,itisasuperkeyofR.Simplifiedtest:TocheckifarelationschemaRisinBCNF,itsufficestocheckonlythedependenciesinthegivensetFforviolationofBCNF,ratherthancheckingalldependenciesinF+.IfnoneofthedependenciesinFcausesaviolationofBCNF,thennoneofthedependenciesinF+willcauseaviolationofBCNFeither.However,simplifiedtestusingonlyFisincorrectwhentestingarelationinadecompositionofRConsiderR=(A,B,C,D,E),withF={AB,BCD}DecomposeRintoR1=(A,B)andR2=(A,C,D,E)NeitherofthedependenciesinFcontainonlyattributesfrom(A,C,D,E)sowemightbemisleadintothinkingR2satisfiesBCNF.Infact,dependencyACDinF+showsR2isnotinBCNF. TestingDecompositionforBCNFTocheckifarelationRiinadecompositionofRisinBCNF,EithertestRiforBCNFwithrespecttotherestrictionofFtoRi(thatis,allFDsinF+thatcontainonlyattributesfromRi)orusetheoriginalsetofdependenciesFthatholdonR,butwiththefollowingtest:foreverysetofattributesRi,checkthat+(theattributeclosureof)eitherincludesnoattributeofRi-,orincludesallattributesofRi.IftheconditionisviolatedbysomeinF,thedependency(+-)RicanbeshowntoholdonRi,andRiviolatesBCNF.WeuseabovedependencytodecomposeRi BCNFDecompositionAlgorithmresult:={R};done:=false;computeF+;while(notdone)doif(thereisaschemaRiinresultthatisnotinBCNF)thenbeginletbeanontrivialfunctionaldependencythatholdsonRisuchthatRiisnotinF+,and=;result:=(result–Ri)(Ri–)(,);endelsedone:=true;Note:eachRiisinBCNF,anddecompositionislossless-join. ExampleofBCNFDecompositionR=(A,B,C)F={ABBC}Key={A}RisnotinBCNF(BCbutBisnotsuperkey)DecompositionR1=(B,C)R2=(A,B) ExampleofBCNFDecompositionclass(course_id,title,dept_name,credits,sec_id,semester,year,building,room_number,capacity,time_slot_id)Functionaldependencies:course_id→title,dept_name,creditsbuilding,room_number→capacitycourse_id,sec_id,semester,year→building,room_number,time_slot_idAcandidatekey{course_id,sec_id,semester,year}.BCNFDecomposition:course_id→title,dept_name,creditsholdsbutcourse_idisnotasuperkey.Wereplaceclassby:course(course_id,title,dept_name,credits)class-1(course_id,sec_id,semester,year,building,room_number,capacity,time_slot_id) BCNFDecomposition(Cont.)courseisinBCNFHowdoweknowthis?building,room_number→capacityholdsonclass-1but{building,room_number}isnotasuperkeyforclass-1.Wereplaceclass-1by:classroom(building,room_number,capacity)section(course_id,sec_id,semester,year,building,room_number,time_slot_id)classroomandsectionareinBCNF. BCNFandDependencyPreservationR=(J,K,L)F={JKLLK}Twocandidatekeys=JKandJLRisnotinBCNFAnydecompositionofRwillfailtopreserveJKLThisimpliesthattestingforJKLrequiresajoinItisnotalwayspossibletogetaBCNFdecompositionthatisdependencypreserving ThirdNormalForm:MotivationTherearesomesituationswhereBCNFisnotdependencypreserving,andefficientcheckingforFDviolationonupdatesisimportantSolution:defineaweakernormalform,calledThirdNormalForm(3NF)Allowssomeredundancy(withresultantproblems;wewillseeexampleslater)Butfunctionaldependenciescanbecheckedonindividualrelationswithoutcomputingajoin.Thereisalwaysalossless-join,dependency-preservingdecompositioninto3NF. 3NFExampleRelationdept_advisor:dept_advisor(s_ID,i_ID,dept_name)F={s_ID,dept_namei_ID,i_IDdept_name}Twocandidatekeys:s_ID,dept_name,andi_ID,s_IDRisin3NFs_ID,dept_namei_IDs_IDdept_nameisasuperkeyi_IDdept_namedept_nameiscontainedinacandidatekey Redundancyin3NFJj1j2j3nullLl1l1l1l2Kk1k1k1k2repetitionofinformation(e.g.,therelationshipl1,k1)(i_ID,dept_name)needtousenullvalues(e.g.,torepresenttherelationshipl2,k2wherethereisnocorrespondingvalueforJ).(i_ID,dept_nameI)ifthereisnoseparaterelationmappinginstructorstodepartmentsThereissomeredundancyinthisschemaExampleofproblemsduetoredundancyin3NFR=(J,K,L)F={JKL,LK} Testingfor3NFOptimization:NeedtocheckonlyFDsinF,neednotcheckallFDsinF+.Useattributeclosuretocheckforeachdependency,ifisasuperkey.Ifisnotasuperkey,wehavetoverifyifeachattributeiniscontainedinacandidatekeyofRthistestisrathermoreexpensive,sinceitinvolvefindingcandidatekeystestingfor3NFhasbeenshowntobeNP-hardInterestingly,decompositionintothirdnormalform(describedshortly)canbedoneinpolynomialtime 3NFDecompositionAlgorithmLetFcbeacanonicalcoverforF;i:=0;foreachfunctionaldependencyinFcdoifnoneoftheschemasRj,1jicontainsthenbegini:=i+1;Ri:=endifnoneoftheschemasRj,1jicontainsacandidatekeyforRthenbegini:=i+1;Ri:=anycandidatekeyforR;end/*Optionally,removeredundantrelations*/repeatifanyschemaRjiscontainedinanotherschemaRkthen/*deleteRj*/Rj=R;;i=i-1;return(R1,R2,...,Ri) 3NFDecompositionAlgorithm(Cont.)Abovealgorithmensures:eachrelationschemaRiisin3NFdecompositionisdependencypreservingandlossless-joinProofofcorrectnessisatendofthispresentation(clickhere) 3NFDecomposition:AnExampleRelationschema:cust_banker_branch=(customer_id,employee_id,branch_name,type)Thefunctionaldependenciesforthisrelationschemaare:customer_id,employee_idbranch_name,typeemployee_idbranch_namecustomer_id,branch_nameemployee_idWefirstcomputeacanonicalcoverbranch_nameisextraneousinther.h.s.ofthe1stdependencyNootherattributeisextraneous,sowegetFC=customer_id,employee_idtypeemployee_idbranch_namecustomer_id,branch_nameemployee_id 3NFDecompsitionExample(Cont.)Theforloopgeneratesfollowing3NFschema:(customer_id,employee_id,type)(employee_id,branch_name)(customer_id,branch_name,employee_id)Observethat(customer_id,employee_id,type)containsacandidatekeyoftheoriginalschema,sonofurtherrelationschemaneedsbeaddedAtendofforloop,detectanddeleteschemas,suchas(employee_id,branch_name),whicharesubsetsofotherschemasresultwillnotdependontheorderinwhichFDsareconsideredTheresultantsimplified3NFschemais:(customer_id,employee_id,type)(customer_id,branch_name,employee_id) ComparisonofBCNFand3NFItisalwayspossibletodecomposearelationintoasetofrelationsthatarein3NFsuchthat:thedecompositionislosslessthedependenciesarepreservedItisalwayspossibletodecomposearelationintoasetofrelationsthatareinBCNFsuchthat:thedecompositionislosslessitmaynotbepossibletopreservedependencies. DesignGoalsGoalforarelationaldatabasedesignis:BCNF.Losslessjoin.Dependencypreservation.Ifwecannotachievethis,weacceptoneofLackofdependencypreservationRedundancyduetouseof3NFInterestingly,SQLdoesnotprovideadirectwayofspecifyingfunctionaldependenciesotherthansuperkeys.CanspecifyFDsusingassertions,buttheyareexpensivetotest,(andcurrentlynotsupportedbyanyofthewidelyuseddatabases!)Evenifwehadadependencypreservingdecomposition,usingSQLwewouldnotbeabletoefficientlytestafunctionaldependencywhoselefthandsideisnotakey. MultivaluedDependenciesSupposewerecordnamesofchildren,andphonenumbersforinstructors:inst_child(ID,child_name)inst_phone(ID,phone_number)Ifweweretocombinetheseschemastogetinst_info(ID,child_name,phone_number)Exampledata:(99999,David,512-555-1234)(99999,David,512-555-4321)(99999,William,512-555-1234)(99999,William,512-555-4321)ThisrelationisinBCNFWhy? MultivaluedDependencies(MVDs)LetRbearelationschemaandletRandR.ThemultivalueddependencyholdsonRifinanylegalrelationr(R),forallpairsfortuplest1andt2inrsuchthatt1[]=t2[],thereexisttuplest3andt4inrsuchthat:t1[]=t2[]=t3[]=t4[]t3[]=t1[]t3[R–]=t2[R–]t4[]=t2[]t4[R–]=t1[R–] MVD(Cont.)Tabularrepresentationof ExampleLetRbearelationschemawithasetofattributesthatarepartitionedinto3nonemptysubsets.Y,Z,WWesaythatYZ(YmultideterminesZ)ifandonlyifforallpossiblerelationsr(R)randrthenrandrNotethatsincethebehaviorofZandWareidenticalitfollowsthatYZifYW Example(Cont.)Inourexample:IDchild_nameIDphone_numberTheaboveformaldefinitionissupposedtoformalizethenotionthatgivenaparticularvalueofY(ID)ithasassociatedwithitasetofvaluesofZ(child_name)andasetofvaluesofW(phone_number),andthesetwosetsareinsomesenseindependentofeachother.Note:IfYZthenYZIndeedwehave(inabovenotation)Z1=Z2Theclaimfollows. UseofMultivaluedDependenciesWeusemultivalueddependenciesintwoways:1.Totestrelationstodeterminewhethertheyarelegalunderagivensetoffunctionalandmultivalueddependencies2.Tospecifyconstraintsonthesetoflegalrelations.Weshallthusconcernourselvesonlywithrelationsthatsatisfyagivensetoffunctionalandmultivalueddependencies.Ifarelationrfailstosatisfyagivenmultivalueddependency,wecanconstructarelationsrthatdoessatisfythemultivalueddependencybyaddingtuplestor. TheoryofMVDsFromthedefinitionofmultivalueddependency,wecanderivethefollowingrule:If,thenThatis,everyfunctionaldependencyisalsoamultivalueddependencyTheclosureD+ofDisthesetofallfunctionalandmultivalueddependencieslogicallyimpliedbyD.WecancomputeD+fromD,usingtheformaldefinitionsoffunctionaldependenciesandmultivalueddependencies.Wecanmanagewithsuchreasoningforverysimplemultivalueddependencies,whichseemtobemostcommoninpracticeForcomplexdependencies,itisbettertoreasonaboutsetsofdependenciesusingasystemofinferencerules(seeAppendixC). FourthNormalFormArelationschemaRisin4NFwithrespecttoasetDoffunctionalandmultivalueddependenciesifforallmultivalueddependenciesinD+oftheform,whereRandR,atleastoneofthefollowinghold:istrivial(i.e.,or=R)isasuperkeyforschemaRIfarelationisin4NFitisinBCNF RestrictionofMultivaluedDependenciesTherestrictionofDtoRiisthesetDiconsistingofAllfunctionaldependenciesinD+thatincludeonlyattributesofRiAllmultivalueddependenciesoftheform(Ri)whereRiandisinD+ 4NFDecompositionAlgorithmresult:={R};done:=false;computeD+;LetDidenotetherestrictionofD+toRiwhile(notdone)if(thereisaschemaRiinresultthatisnotin4NF)thenbeginletbeanontrivialmultivalueddependencythatholdsonRisuchthatRiisnotinDi,and;result:=(result-Ri)(Ri-)(,);endelsedone:=true;Note:eachRiisin4NF,anddecompositionislossless-join ExampleR=(A,B,C,G,H,I)F={ABBHICGH}Risnotin4NFsinceABandAisnotasuperkeyforRDecompositiona)R1=(A,B)(R1isin4NF)b)R2=(A,C,G,H,I)(R2isnotin4NF,decomposeintoR3andR4)c)R3=(C,G,H)(R3isin4NF)d)R4=(A,C,G,I)(R4isnotin4NF,decomposeintoR5andR6)ABandBHIAHI,(MVDtransitivity),andandhenceAI(MVDrestrictiontoR4)e)R5=(A,I)(R5isin4NF)f)R6=(A,C,G)(R6isin4NF) FurtherNormalFormsJoindependenciesgeneralizemultivalueddependenciesleadtoproject-joinnormalform(PJNF)(alsocalledfifthnormalform)Aclassofevenmoregeneralconstraints,leadstoanormalformcalleddomain-keynormalform.Problemwiththesegeneralizedconstraints:arehardtoreasonwith,andnosetofsoundandcompletesetofinferencerulesexists.Hencerarelyused OverallDatabaseDesignProcessWehaveassumedschemaRisgivenRcouldhavebeengeneratedwhenconvertingE-Rdiagramtoasetoftables.Rcouldhavebeenasinglerelationcontainingallattributesthatareofinterest(calleduniversalrelation).NormalizationbreaksRintosmallerrelations.Rcouldhavebeentheresultofsomeadhocdesignofrelations,whichwethentest/converttonormalform. ERModelandNormalizationWhenanE-Rdiagramiscarefullydesigned,identifyingallentitiescorrectly,thetablesgeneratedfromtheE-Rdiagramshouldnotneedfurthernormalization.However,inareal(imperfect)design,therecanbefunctionaldependenciesfromnon-keyattributesofanentitytootherattributesoftheentityExample:anemployeeentitywithattributesdepartment_nameandbuilding,andafunctionaldependencydepartment_namebuildingGooddesignwouldhavemadedepartmentanentityFunctionaldependenciesfromnon-keyattributesofarelationshipsetpossible,butrare---mostrelationshipsarebinary DenormalizationforPerformanceMaywanttousenon-normalizedschemaforperformanceForexample,displayingprereqsalongwithcourse_id,andtitlerequiresjoinofcoursewithprereqAlternative1:UsedenormalizedrelationcontainingattributesofcourseaswellasprereqwithallaboveattributesfasterlookupextraspaceandextraexecutiontimeforupdatesextracodingworkforprogrammerandpossibilityoferrorinextracodeAlternative2:useamaterializedviewdefinedascourseprereqBenefitsanddrawbackssameasabove,exceptnoextracodingworkforprogrammerandavoidspossibleerrors OtherDesignIssuesSomeaspectsofdatabasedesignarenotcaughtbynormalizationExamplesofbaddatabasedesign,tobeavoided:Insteadofearnings(company_id,year,amount),useearnings_2004,earnings_2005,earnings_2006,etc.,allontheschema(company_id,earnings).AboveareinBCNF,butmakequeryingacrossyearsdifficultandneedsnewtableeachyearcompany_year(company_id,earnings_2004,earnings_2005,earnings_2006)AlsoinBCNF,butalsomakesqueryingacrossyearsdifficultandrequiresnewattributeeachyear.Isanexampleofacrosstab,wherevaluesforoneattributebecomecolumnnamesUsedinspreadsheets,andindataanalysistools ModelingTemporalDataTemporaldatahaveanassociationtimeintervalduringwhichthedataarevalid.AsnapshotisthevalueofthedataataparticularpointintimeSeveralproposalstoextendERmodelbyaddingvalidtimetoattributes,e.g.,addressofaninstructoratdifferentpointsintimeentities,e.g.,timedurationwhenastudententityexistsrelationships,e.g.,timeduringwhichaninstructorwasassociatedwithastudentasanadvisor.ButnoacceptedstandardAddingatemporalcomponentresultsinfunctionaldependencieslikeIDstreet,citynottohold,becausetheaddressvariesovertimeAtemporalfunctionaldependencyXYholdsonschemaRifthefunctionaldependencyXYholdsonallsnapshotsforalllegalinstancesr(R).t ModelingTemporalData(Cont.)Inpractice,databasedesignersmayaddstartandendtimeattributestorelationsE.g.,course(course_id,course_title)isreplacedbycourse(course_id,course_title,start,end)Constraint:notwotuplescanhaveoverlappingvalidtimesHardtoenforceefficientlyForeignkeyreferencesmaybetocurrentversionofdata,ortodataatapointintimeE.g.,studenttranscriptshouldrefertocourseinformationatthetimethecoursewastaken EndofChapter ProofofCorrectnessof3NFDecompositionAlgorithm Correctnessof3NFDecompositionAlgorithm3NFdecompositionalgorithmisdependencypreserving(sincethereisarelationforeveryFDinFc)DecompositionislosslessAcandidatekey(C)isinoneoftherelationsRiindecompositionClosureofcandidatekeyunderFcmustcontainallattributesinR.FollowthestepsofattributeclosurealgorithmtoshowthereisonlyonetupleinthejoinresultforeachtupleinRi Correctnessof3NFDecompositionAlgorithm(Cont’d.)Claim:ifarelationRiisinthedecompositiongeneratedbytheabovealgorithm,thenRisatisfies3NF.LetRibegeneratedfromthedependencyLetBbeanynon-trivialfunctionaldependencyonRi.(WeneedonlyconsiderFDswhoseright-handsideisasingleattribute.)Now,Bcanbeineitherorbutnotinboth.Considereachcaseseparately. Correctnessof3NFDecomposition(Cont’d.)Case1:IfBin:Ifisasuperkey,the2ndconditionof3NFissatisfiedOtherwisemustcontainsomeattributenotinSinceBisinF+itmustbederivablefromFc,byusingattributeclosureon.Attributeclosurenothaveused.Ifithadbeenused,mustbecontainedintheattributeclosureof,whichisnotpossible,sinceweassumedisnotasuperkey.Now,using(-{B})andB,wecanderiveB(since,andBsinceBisnon-trivial)Then,Bisextraneousintheright-handsideof;whichisnotpossiblesinceisinFc.Thus,ifBisinthenmustbeasuperkey,andthesecondconditionof3NFmustbesatisfied. Correctnessof3NFDecomposition(Cont’d.)Case2:Bisin.Sinceisacandidatekey,thethirdalternativeinthedefinitionof3NFistriviallysatisfied.Infact,wecannotshowthatisasuperkey.Thisshowsexactlywhythethirdalternativeispresentinthedefinitionof3NF.Q.E.D. Figure8.02 Figure8.03 Figure8.04 Figure8.05 Figure8.06 Figure8.14 Figure8.15 Figure8.17'