数据结构课件PPT110章全第七章图.ppt 65页

1.12 MB
2022-04-29 14:33:30 发布

数据结构课件PPT110章全第七章图.ppt

关闭预览

65页
当前文档由用户上传发布，收益归属用户

下载提示
文本预览

1、本文档共5页，可阅读全部内容。
2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，可选择认领，认领后既往收益都归您。
3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形，可联系本站下载客服投诉处理。
文档侵权举报电话：19940600175。

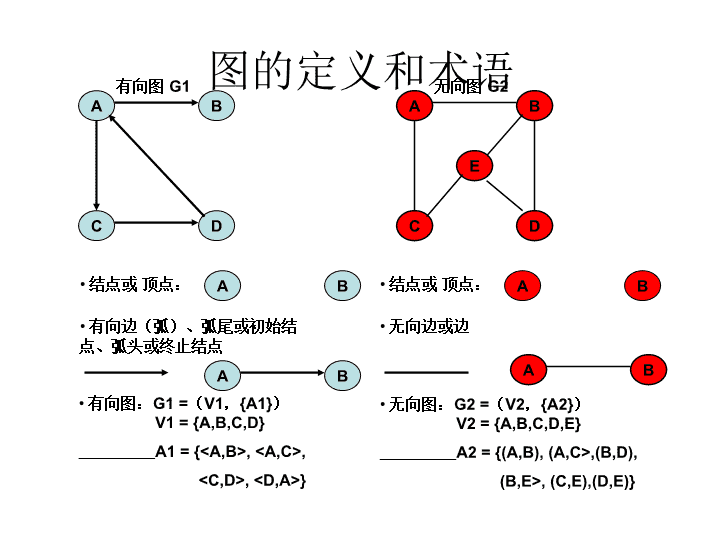
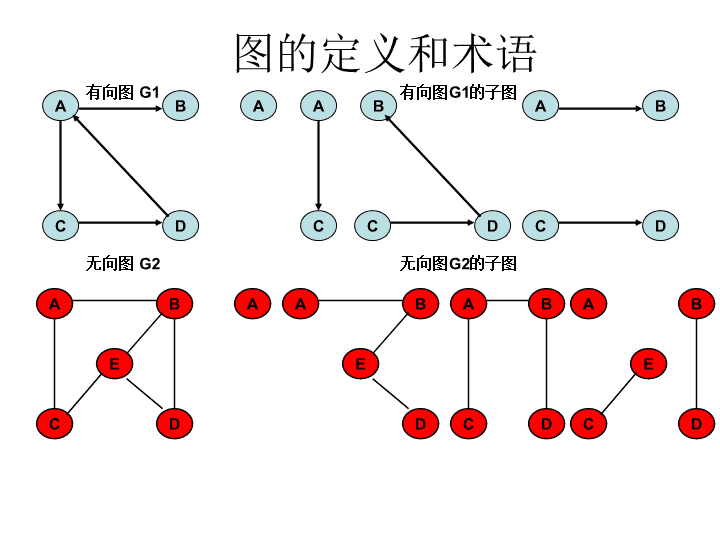
'1、图的定义和术语2、图的存储结构3、图的遍历4、图的连通性问题5、有向无环图及其应用6、最短路径第七章图图的定义和术语ABCDABCDE有向图G1无向图G2结点或顶点：有向边（弧）、弧尾或初始结点、弧头或终止结点ABAB有向图：G1=（V1，{A1}）V1={A,B,C,D}A1={,,,}结点或顶点：无向边或边AB无向图：G2=（V2，{A2}）V2={A,B,C,D,E}A2={(A,B),(A,C>,(B,D),(B,E>,(C,E),(D,E)}AB 图的定义和术语ABCD无向图G2ABCDACABCD有向图G1的子图ABCDEABDEAABCDABCDE无向图G2的子图有向图G1 图的定义和术语无向图的连通性ABCDE路径：在无向图G=(V,{E})中由顶点v至v‘’的顶点序列。回路或环：第一个顶点和最后一个顶点相同的路径。简单回路或简单环：除第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路。连通：顶点v至v‘’之间有路径存在连通图：无向图图G的任意两点之间都是连通的，则称G是连通图。连通分量：极大连通子图FGIJLHMKABCDEHMFGIJLK无向图G无向图G的三个连通分量图的定义和术语有向图的连通性路径：在有向图G=(V,{E})中由顶点v经有向边至v‘’的顶点序列。回路或环：第一个顶点和最后一个顶点相同的路径。简单回路或简单环：除第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路。连通：顶点v至v‘’之间有路径存在强连通图：有向图图G的任意两点之间都是连通的，则称G是强连通图。强连通分量：极大连通子图有向图G有向图G的两个强连通分量ABCDABCD 图的定义和术语生成树：极小连通子图。包含图的所有n个结点，但只含图的n-1条边。在生成树中添加一条边之后，必定会形成回路或环。ABCDEHMABCDEHM无向图G无向图G的生成树图的定义和术语完全图：有n(n-1)/2条边的无向图。其中n是结点个数。有向完全图：有n(n-1)条边的有向图。其中n是结点个数。边的权值，边有权的图称之为网络。邻接点：无向图结点的度有向图结点的出度和入度ABCDEHM无向图G1图的其它术语有向图G2ABCD 图的存储结构图的四种常用的存储形式：邻接矩阵和加权邻接矩阵（labeledadjacencymatrix）邻接表十字链表邻接多重表1、邻接矩阵和加权邻接矩阵（labeledadjacencymatrix）ABCD无权值的有向图的邻接矩阵设有向图具有n个结点，则用n行n列的布尔矩阵A表示该有向图；并且A[i,j]=1,如果i至j有一条有向边；A[I,j]=0如果i至j没有一条有向边注意：A[i,i]=0。出度:i行之和。入度:j列之和。表示成右图矩阵0110000000011000 图的存储结构1、邻接矩阵和加权邻接矩阵（labeledadjacencymatrix）（续）无权值的无向图的邻接矩阵设无向图具有n个结点，则用n行n列的布尔矩阵A表示该无向图；并且A[i,j]=1,如果i至j有一条无向边；A[I,j]=0如果i至j没有一条无向边注意：A[i,i]=0。i结点的度:i行或i列之和。上三角矩阵或下三角矩阵。表示成右图矩阵0110010011100010100101110ABCDE 图的存储结构1、邻接矩阵和加权邻接矩阵（labeledadjacencymatrix）（续）有向图的加权邻接矩阵设有向图具有n个结点，则用n行n列的矩阵A表示该有向图；并且A[i,j]=a,如果i至j有一条有向边且它的权值为a。A[i,j]=‘空或其它标志；如果i至j没有一条有向边。ABCD表示成右图矩阵abbbaaaaabbb优点：判断任意两点之间是否有边方便，仅耗费O(1)时间。缺点：即使<j是否有边，最坏需耗费O(n)时间。无向图同一条边表示两次边表空间浪费一倍。有向图中寻找进入某结点的边，非常困难。datafirstarc结点表中的结点的表示：用数组data:结点的数据场，保存结点的数据值。firstarc:结点的指针场，给出自该结点出发的的第一条边的边结点的地址。图的存储结构2、邻接表（adjacencylist）datafirstarc结点表中的结点的表示：续用单链表data:结点的数据场，保存结点的数据值。firstarc:结点的指针场，给出自该结点出发的的第一条边的边结点的地址。nextvex:结点的指针场，给出该结点的下一结点的地址。nextvexinfoadjvexnextarc边结点表中的结点的表示：info:边结点的数据场，保存边的权值等。adjvex:边结点的指针场，给出本条边依附的另一结点（非出发结点）的地址。nextarc:结点的指针场，给出自该结点出发的的下一条边的边结点的地址。图的存储结构2、邻接表（adjacencylist）实例：ABCD无向图G2ABCDE向图G1ABCD23141234nullnullnullnulldatafirstarcadjvexnextvexAB2312345nulldatafirstarc14152523CDE54nullnullnullnullAdjvex指针场之值为相应结点数的组元素的下标!!!六条边却用了12个边结点!!!改进：建立邻接多重表寻找进入结点的边非常困难!!!改进：建立逆邻接表或十字链表adjvexnextvex 图的存储结构2、邻接表（adjacencylist）逆邻接表实例：ABCD有向图G1AB431234null113CDnullnullnull 图的存储结构3、十字链表datafirstinfirstoutinfotailvexheadvex边结点表中的结点的表示：结点表中的结点的表示：data:结点的数据场，保存结点的数据值。firstin:结点的指针场，给出自该结点出发的的第一条边的边结点的地址。firstout:结点的指针场，给出进入该结点的第一条边的边结点的地址。info:边结点的数据场，保存边的权值等。hlinktlinktailvex:本条边的出发结点的地址。headvex:本条边的终止结点的地址。hlink:终止结点相同的边中的下一条边的地址。tlink:出发结点相同的边中的下一条边的地址。图的存储结构3、十字链表实例：ABCD向图G10123ABCD01022220033331∧∧∧∧∧∧∧∧datafirstinfirstouttailvexheadvexhlinktlink用途：用于有向图，查询进入结点和离开结点的边容易。图的存储结构4、邻接多重表datafirstedgemarkivexilink边结点表中的结点的表示：结点表中的结点的表示：data:结点的数据场，保存结点的数据值。firstedge:结点的指针场，给出自该结点出发的的第一条边的边结点的地址。info:边结点的数据场，保存边的权值等。mark:边结点的标志域，用于标识该条边是否被访问过。jvexinfoivex:本条边依附的一个结点的地址。ilink:依附于该结点（地址由ivex给出）的边中的下一条边的的地址。jlinkjvex:本条边依附的另一个结点的地址。jlink:依附于该结点（地址由jvex给出）的边中的下一条边的的地址。图的存储结构4、邻接多重表实例：无向图G2用途：用于无向图，边表中的边结点只需存放一次，节约内存。ABCDEAB12345datafirstedgeCDE123552421345∧∧∧∧markivexilinkjvexjlink∧ 图的遍历图的两种常见的遍历形式：深度优先搜索广度优先搜索1、深度优先搜索注意：每个结点只能被访问一次，又因为一个结点可以和其它的任何结点相邻接，为了避免对一个结点的重复访问，必须对访问过的结点加以标记。结点的邻接结点的次序是任意的，因此深度优先搜索的序列可能有多种。深度优先搜索类似于树的前序周游。访问方式：1、选中第一个被访问的结点。2、对结点作已访问过的标志。3、依次从结点的未被访问过的第一个、第二个、第三个……邻接结点出发，进行深度优先搜索。转向2。4、如果还有顶点未被访问，则选中一个起始结点，转向2。5、所有的结点都被访问到，则结束。图的遍历1、深度优先搜索:续有向图的实例：为了说明问题，邻接结点的访问次序以序号为准。序号小的先访问。如：结点5的邻接结点有两个6、7，则先访问结点6，再访问结点7。56724135672314·······从结点出发的搜索序列：5、6、2、3、1、4、7适用的数据结构：栈51243····从结点出发的搜索序列：1、2、3、4没有搜索到所有的结点，必须另选图中未访问过的结点，继续进行搜索。1 图的遍历1、深度优先搜索:续搜索的实现。使用的变量说明：Booleanvisited[MAX];//用于标识结点是否已被访问过Status(*VisitFunc)(intv);//函数变量voidDFSTraverse(GraphG,Status(*VisitFunc)(intv));{VisitFunc=Visit;for(v=0;v后件的序号序列：3、1、2、4、6、5、7不合乎拓扑排序的要求序号1、2、3、4、5、6、7元素3的序号1（后件）<元素1（前件）的序号2 有向无环图及其应用2、拓扑排序（TopologicalSort）实例：下述集合M代表课程的集合，其中，1代表数学，2代表程序设计，3代表离散数学，4代表汇编程序设计，5代表数据结构，6代表结构程序设计,7代表编译原理。关系R课程学习的先后关系，如数学必须在离散数学之前学习。要求排一张学习的先后次序表。132756413275641324657 有向无环图及其应用2、拓扑排序（TopologicalSort）算法（使用邻接矩阵）：1327564011000000001110000101000000000000010000001000000012345671234567算法的执行步骤：1、找到全为零的第j列，输出j2、将第j行的全部元素置为零3、找到全为零的第k列，输出k4、将第k行的全部元素置为零…………………反复执行3、4；直至所有元素输出完毕。0000000000011100001010000000000000100000010000000 有向无环图及其应用2、拓扑排序（TopologicalSort）算法（使用邻接表）：1327564算法的执行步骤：1、用一个数组记录每个结点的入度。将入度为零的结点进栈。2、将栈中入度为零的结点V输出。3、根据邻接表找到结点V的所有的邻接结点，并将这些邻接结点的入度减一。如果某一结点的入度变为零，则进栈。4、反复执行2、3；直至栈空为止。…………………次序执行结束，如果输出结点数等于图的结点总数，则有向图有环，否则有向图有环。12120123456null34463455nullnullnull6766nullnullnull01012345611213indegree0栈有向无环图及其应用2、拓扑排序（TopologicalSort）算法（使用邻接表）的程序：1327564StatusTopologicalsort（ALGraphG）{findinDegree（G，indegree）;Initstack（S）；for（i=0;inextarc）;{k=p->adjnexr;if（!（--indegree[k]））Push（S,k）;}}if（countnextarc）;{k=p->adjnexr;if（!（--indegree[k]））Push（S,k）;if（ve[j]+*（p->info）>ve[k]）ve[k]=ve[j]+*（p->info）;}}}if（countp1，同假设矛盾，不可能。Dijkstra算法:边的权值不可以为负值。V0V1V2100-995STVp1p2p3p4 Floyd算法的求解过程设C为n行n列的代价矩阵，c[i,j]为i--->j的权值。如果i=j；那么c[i,j]=0。如果i和j之间无有向边；则c[i,j]=∞1、使用n行n列的矩阵A用于计算最短路径。初始时，A[i,j]=c[i,j]2、进行n次迭代在进行第k次迭代时，我们将使用如下的公式：Ak-1[i,j]Ak[i,j]=MINAk-1[i,k]+Ak-1[k,j]注意：第k次迭代时，针对结点k进行。原Ak-1矩阵的第k行，第k列保持不变。左上至右下的对角线元素也不变。最短路径2、每一对顶点之间的最短路径：Floyd算法V1V2加权有向图：求各结点之间的最短路径V05382jkiAk-1[i,k]Ak-1[k,j]Ak-1[i,j]08530∞∞20012012右图的代价矩阵c 最短路径2、每一对顶点之间的最短路径：Floyd算法V1V2实例及求解过程:V05382Floyd算法的求解过程设C为n行n列的代价矩阵，c[i,j]为i--->j的权值。如果i=j；那么c[i,j]=0。如果i和j之间无有向边；则c[i,j]=∞1、使用n行n列的矩阵A用于计算最短路径。初始时，A[i,j]=c[i,j]2、进行n次迭代在进行第k次迭代时，我们将使用如下的公式：Ak-1[i,j]Ak[i,j]=MINAk-1[i,k]+Ak-1[k,j]注意：第k次迭代时，针对结点k进行。原Ak-1矩阵的第k行，第k列保持不变。左上至右下的对角线元素也不变。08530∞∞2001201208530∞∞20085308∞20075308520085308520A0A2A1A初值请看实例最短路径2、每一对顶点之间的最短路径：Floyd算法算法的程序实现:Floyd算法的程序的简单描述：inti,jk;//代表结点for(i=0;iV1->V0可以有许多圈。作业题集7.1,7.3,7.15,7.16题集7.25,7.27'

数据结构课件PPT110章全第七章图.ppt 65页