不等式的性质课件PPT25张（人教版七年级下数学）.ppt 25页

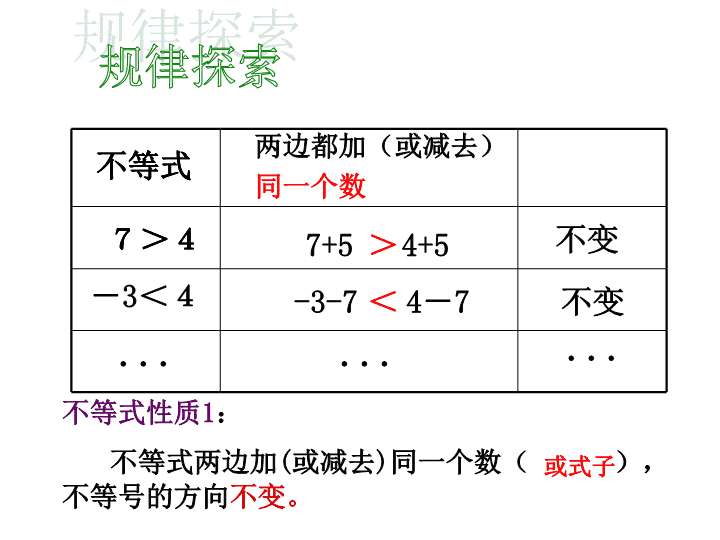
'9.1.2不等式的性质 等式基本性质1：等式的两边都加上（或减去）同一个整式，等式仍旧成立等式基本性质2：等式的两边都乘以（或除以）同一个不为0的数，等式仍旧成立如果a=b,那么a±c=b±c如果a=b,那么ac=bc或（c≠0）， 规律探索不等式７＞４－3＜４7+54+5-3-74－7不变不变两边都加（或减去）同一个数不等式７＞４.........不等式性质1：不等式两边加(或减去)同一个数（），不等号的方向不变。或式子＞＜ 不等式的性质1不等式的两边加（或减）同一个数(或式子)，不等号的方向不变.如果a＞b，那么a±cb±c字母表示为：﹥ 规律探索不等式７＞４－8＜４7×54×5-8÷24÷2不变不变两边都乘（或除以）同一个正数不等式７＞４.........不等式性质2：不等式两边乘()同一个正数，不等号的方向不变。或除以＞＜ 不等式的性质2不等式的两边乘（或除以）同一个正数，不等号的方向不变.如果a＜b,c>0那么acbc，字母表示为：﹤﹤ 规律探索不等式７＞４－8＜４7×(-5)4×(-5)-8÷（-2）4÷（-2）改变改变两边都乘（或除以）同一个负数不等式７＞４.........不等式性质3：不等式两边乘()同一个负数，不等号的方向改变。或除以<> 不等式的性质3不等式的两边乘（或除以）同一个负数，不等号的方向改变必须把不等号的方向改变如果a＞b，c＜0那么acbc，字母表示为：类比推导﹤﹤ 不等式性质1：不等式两边加(减去)同一个正数，不等号的方向不变。不等式性质2：不等式两边乘(或除以)同一个正数，不等号的方向不变。不等式性质3：不等式两边乘(或除以)同一个负数，不等号的方向改变。 针对练习针对练习(1)如果x-5>4，那么两边都可得到x>9(2)如果在-7<8的两边都加上9可得到(3)如果在5>-2的两边都加上a+2可得到(4)如果在-3>-4的两边都乘以7可得到(5)如果在8>0的两边都乘以8可得到(6)如果在的两边都乘以14可得到X7>2+X2加上52<17a+7>a-21>-2864>02x>28+7x (1)如果在不等式8>0的两边都乘以―8可得到(2)如果-3x>9，那么两边都除以―3可得到(3)设m>n,用“>”或“<”填空：m-5n-5（根据不等式的性质）-6m-6n（根据不等式的性质）针对练习-64<0x<-3>1<3 例1：判断下列各题的推导是否正确？为什么(学生口答)(1)因为7.5＞5.7，所以-7.5＜-5.7；(2)因为a+8＞4，所以a＞-4；(3)因为4a＞4b，所以a＞b；(4)因为-1＞-2，所以-a-1＞-a-2；(5)因为3＞2，所以3a＞2a．答：．(1)正确，根据不等式基本性质3．(2)正确，根据不等式基本性质1．(3)正确，根据不等式基本性质2．(4)正确，根据不等式基本性质1．(5)不对，应分情况逐一讨论．当a＞0时，3a＞2a．(不等式基本性质2)当a=0时，3a=2a．当a＜0时，3a＜2a．(不等式基本性质3) 例2：设a＞b，用“＜”或“＞”填空并口答是根据哪一条不等式基本性质。（1）a-3____b-3；（2）a÷3____b÷3（3）0.1a____0.1b;(4)-4a____-4b(5)2a+3____2b+3;(6)(m2+1)a____(m2+1)b(m为常数)＞＞＞＞＞＜ 练习：已知a＜0，用“＜”或“＞”号填空：(1)a+2____2；(2)a-1_____-1；(3)3a______0；(4)-a/4______0;(5)a2_____0;(6)a3______0(7)a-1______0；(8)|a|______0．答：(1)a+2＜2，根据不等式基本性质1．(2)a-1＜-1，根据不等式基本性质1．(3)3a＜0，根据不等式基本性质2．(5)因为a＜0，两边同乘以a＜0，由不等式基本性质3，得a2＞0．(6)因为a＜0，两边同乘以a2＞0，由不等式基本性质2，得a3＜0．(7)因为a＜0，两边同加上-1，由不等式基本性质1，得a-1＜-1．又已知，-1＜0，所以a-1＜0．(8)因为a＜0，所以a≠0，所以|a|＞0．(4)-a/4>0,根据不等式基本性质3． （1）（2）（3）（4）（5）1、判断（√）（×）（√）（×）（×） 2、判断正误：（１）如果a＞b，那么ac＞bc。（２）如果a＞b，那么ac2＞bc2。（３）如果ac2＞bc2,那么a＞b。×× 例3利用不等式的性质解下列不等式．(1)x-７＞26(2)-4x﹥3(3)3x<2x+1Zx.xk 例１　利用不等式的性质解下列不等式用数轴表示解集．(1)x-７＞26我是最棒的☞解：根据不等式性质1，得X-7+7>26+7X>33330(2)-4x﹥3解：根据不等式性质3，得X<―43解未知数为x的不等式，就是要使不等式逐步化为x﹥a或x﹤a的形式．0 (3)3x<2x+13x-2x﹤2x+1-2xx﹤1这个不等式的解在数轴上的表示注意：解不等式时也可以“移项”，即把不等式的一边的某项变号后移到另一边，而不改变不等号的方向．01解：根据不等式性质1，得3x-2x﹤1 自我检测利用不等式的性质解下列不等式用数轴表示解集．(1)x+3>-1解：根据不等式性质1,得X<-7(3)4x>-12解：根据不等式性质2，得X>-30-4-700-3解：根据不等式性质1，得X>-4(2)6x<5x-7 ２(4)－x﹥503x﹥75这个不等式的解集在数轴的表示如图０75解：2为了使不等式－x﹥50中不等号的一边变为x，根据不等式的性质２，不等式的两边都乘　不等号的方向不变，得332将未知数系数化1 (5)解：不等式两边同时乘以12，得2(5x+1)-2×12>3(x-5)10x+2-24>3x-1510x-3x>24-2-157x>7X>1去分母拆括号移项合并同类项系数化101 新情境题以下不等式中,不等号用对了么?(1)3-a<6-a(2)3a<6a解：(1)3<6,根据不等式的性质1将不等式两边同时减a,3-a<6-a(2)3<6,当a>0时,根据不等式的性质2,3a<6a当a<0时,根据不等式的性质3,3a>6a 如果关于x的不等式(1-a)x>1-a的解集为x<1,那么请给出一个符合题意a的值解：由(1-a)x>1-a，不等式两边同时除以1-a，得到x<1不等号方向改变了，由不等式的性质3可知1-a<0,a>1可以取a=2 想一想:'