习题课高等数学微积分课件PPT课件.ppt 58页

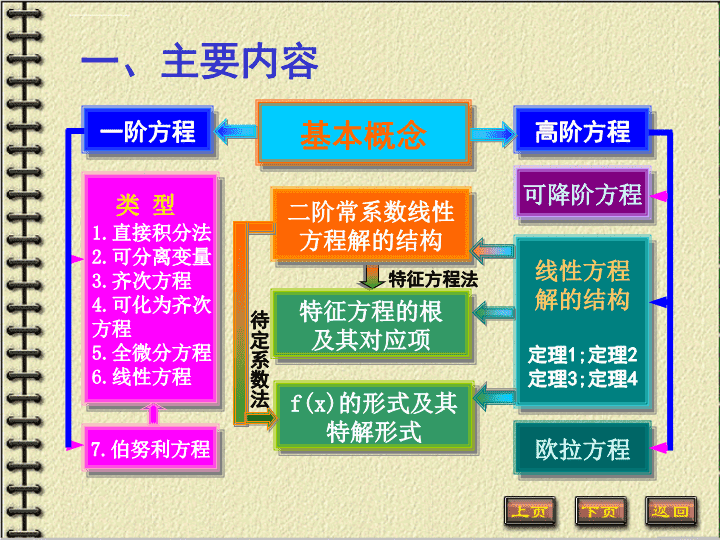
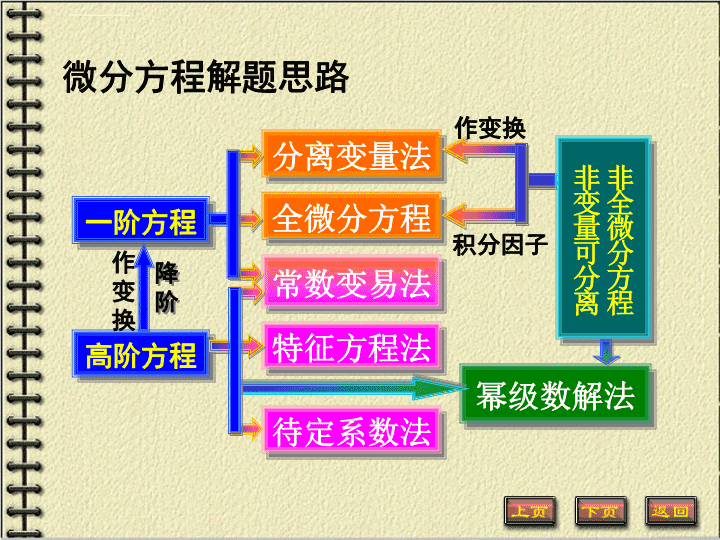
'基本概念一阶方程类型1.直接积分法2.可分离变量3.齐次方程4.可化为齐次方程5.全微分方程6.线性方程7.伯努利方程可降阶方程线性方程解的结构定理1;定理2定理3;定理4欧拉方程二阶常系数线性方程解的结构特征方程的根及其对应项f(x)的形式及其特解形式高阶方程待定系数法特征方程法一、主要内容 微分方程解题思路一阶方程高阶方程分离变量法全微分方程常数变易法特征方程法待定系数法非全微分方程非变量可分离幂级数解法降阶作变换作变换积分因子 1、基本概念微分方程凡含有未知函数的导数或微分的方程叫微分方程．微分方程的阶微分方程中出现的未知函数的最高阶导数的阶数称为微分方程的阶．微分方程的解代入微分方程能使方程成为恒等式的函数称为微分方程的解． 通解如果微分方程的解中含有任意常数，并且任意常数的个数与微分方程的阶数相同，这样的解叫做微分方程的通解．特解确定了通解中的任意常数以后得到的解，叫做微分方程的特解．初始条件用来确定任意常数的条件.初值问题求微分方程满足初始条件的解的问题，叫初值问题． (1)可分离变量的微分方程解法分离变量法2、一阶微分方程的解法(2)齐次方程解法作变量代换 齐次方程．（其中h和k是待定的常数）否则为非齐次方程．(3)可化为齐次的方程解法化为齐次方程． (4)一阶线性微分方程上方程称为齐次的．上方程称为非齐次的.齐次方程的通解为（使用分离变量法）解法 非齐次微分方程的通解为（常数变易法）(5)伯努利(Bernoulli)方程方程为线性微分方程.方程为非线性微分方程. 解法需经过变量代换化为线性微分方程．其中形如(6)全微分方程 注意：解法应用曲线积分与路径无关.用直接凑全微分的方法.通解为 (7)可化为全微分方程形如 公式法:观察法:熟记常见函数的全微分表达式，通过观察直接找出积分因子． 常见的全微分表达式可选用积分因子 3、可降阶的高阶微分方程的解法解法特点型接连积分n次，得通解．型解法代入原方程,得 特点型解法代入原方程,得４、线性微分方程解的结构（1）　二阶齐次方程解的结构: （2）二阶非齐次线性方程的解的结构: ５、二阶常系数齐次线性方程解法n阶常系数线性微分方程二阶常系数齐次线性方程二阶常系数非齐次线性方程解法由常系数齐次线性方程的特征方程的根确定其通解的方法称为特征方程法. 特征方程为 特征方程为特征方程的根通解中的对应项推广：阶常系数齐次线性方程解法 ６、二阶常系数非齐次线性微分方程解法二阶常系数非齐次线性方程解法待定系数法. 7、欧拉方程欧拉方程是特殊的变系数方程，通过变量代换可化为常系数微分方程.的方程(其中形如叫欧拉方程.为常数)， 当微分方程的解不能用初等函数或其积分表达时,常用幂级数解法.8、幂级数解法 二、典型例题例1解原方程可化为 代入原方程得分离变量两边积分所求通解为 例2解原式可化为原式变为对应齐方通解为一阶线性非齐方程伯努利方程 代入非齐方程得原方程的通解为利用常数变易法 例3解方程为全微分方程. (1)利用原函数法求解:故方程的通解为 (2)利用分项组合法求解:原方程重新组合为故方程的通解为 (3)利用曲线积分求解:故方程的通解为 例4解非全微分方程.利用积分因子法:原方程重新组合为 故方程的通解为 例5解代入方程，得故方程的通解为 例6解特征方程特征根对应的齐次方程的通解为设原方程的特解为 原方程的一个特解为故原方程的通解为 由解得所以原方程满足初始条件的特解为 例７解特征方程特征根对应的齐方的通解为设原方程的特解为 由解得 故原方程的通解为由即 例８解（１）　由题设可得：解此方程组，得 （２）　原方程为由解的结构定理得方程的通解为 解例９这是一个欧拉方程．代入原方程得(1) 和(1)对应的齐次方程为(2)(2)的特征方程为特征根为(2)的通解为设(1)的特解为 得(1)的通解为故原方程的通解为 解例10则由牛顿第二定律得 解此方程得代入上式得 测验题 测验题答案 '