最新新人教版第五章相交线与平行线复习课件PPT课件.ppt 65页

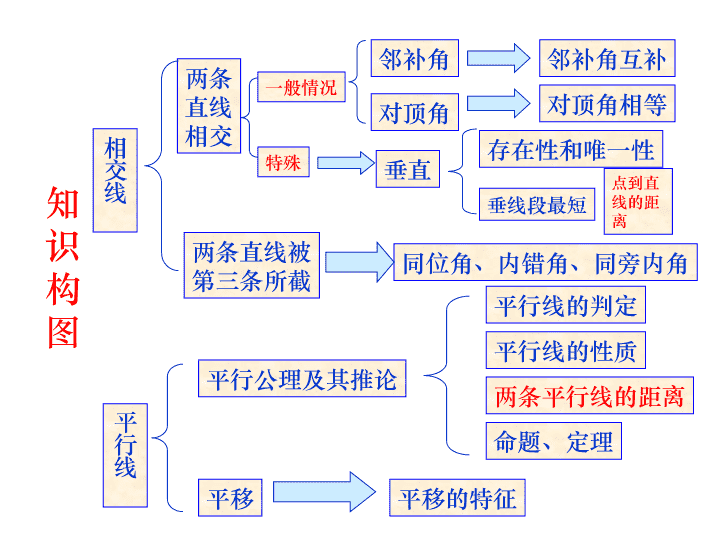
'新人教版第五章相交线与平行线复习课件 1、进一步巩固邻补角、对顶角的概念和性质2、理解垂线、垂线段的概念和性质3、掌握两条直线平行的判定和性质一、学习目标4、通过平移，理解图形平移变换的性质5、能区分命题的题设和结论以及命题的真假 相交线两条直线相交两条直线被第三条所截一般情况邻补角对顶角邻补角互补对顶角相等特殊垂直存在性和唯一性垂线段最短点到直线的距离同位角、内错角、同旁内角平行线平行公理及其推论平行线的判定平行线的性质两条平行线的距离平移平移的特征命题、定理知识构图 1.垂线的定义:两条直线相交，所构成的四个角中，有一个角是90°时，就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。2.垂线的性质:(1)过一点有且只有一条直线与已知直线垂直。(2):直线外一点与直线上各点连结的所有线段中，垂线段最短。简称:垂线段最短。3.点到直线的距离:从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。4.如遇到线段与线段，线段与射线，射线与射线，线段或射线与直线垂直时，特指它们所在的直线互相垂直。5.垂线是直线，垂线段特指一条线段是图形，点到直线距离是指垂线段的长度，是指一个数量，是有单位的。垂线 ┓ABCDOE此题需要正确地应用、对顶角、邻补角、垂直的概念和性质。 OADCB由垂直先找到90°的角，再根据角之间的关系求解。 C∟理由:垂线段最短例3:如图,要把水渠中的水引到水池C中，在渠岸的什么地方开沟，水沟的长度才能最短？请画出图来，并说明理由。 ADCBEF例4:你能量出C到AB的距离,B到AC的距离,A到BC的距离吗? 思考：三角形的三条垂线有什么特点？三角形的三条垂线都交于一点；锐角三角形的三条垂线交点在三角形的内部；直角三角形的三条垂线交点在直角顶点；钝角三角形的三条垂线交点在三角形的外部；例5:你能画出ABC三点到对边的垂线吗？ ABCD在如图所示的三角形中,说出下列点到线段的距离分别是哪一条线段的长度点C到线段AB的距离点A到线段BC的距离点B到线段AC的距离ACCDBCBD是点＿到线段＿＿的距离BCD 平行线的概念:在同一平面内,不相交的两条直线叫做平行线。2.两直线的位置关系:在同一平面内，两直线的位置关系只有两种:(1)相交;(2)平行。3.平行线的基本性质:(1)平行公理(平行线的存在性和唯一性)经过直线外一点，有且只有一条直线与已知直线平行。(2)推论(平行线的传递性)如果两条直线都和第三条直线平行，那么这两条直线也互相平行。4.同位角、内错角、同旁内角的概念同位角、内错角、同旁内角，指的是一条直线分别与两条直线相交构成的八个角中，不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样，总是成对存在着的。平行 1、同位角的位置特征是:2、内错角的位置特征是:3、同旁内角的位置特征是:(1)在截线的同旁，(2)在被截两直线的同方向。(1)在截线的两旁，(2)在被截两直线之间。(1)在截线的同旁，(2)在被截两直线之间。F1375286DCABE4被截线截线三线八角 (1)定义法;在同一平面内不相交的两条直线是平行线。(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。(4)三种角判定(3种方法):在这六种方法中，定义一般不常用。同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。(3)因为a⊥c,a⊥b；所以b//cabCFABCDE1234判定两直线平行的方法有三种: ∠1和∠2不是同位角，如图中的∠1和∠2是同位角吗?为什么?1212∵∠1和∠2无一边共线。∠1和∠2是同位角，∵∠1和∠2有一边共线、同向且不共顶点。练一练 ACBDE12答：∠EAC答：∠DAB答：∠BAC,∠BAE,∠2∠1与哪个角是同旁内角？∠2与哪个角是内错角?例1.∠1与哪个角是内错角？ 证明:∵∠DAC=∠ACB(已知)ABCDEF∴AD//BC(内错角相等,两直线平行)∵∠D+∠DFE=180°(已知)∴AD//EF(同旁内角互补,两直线平行)∴EF//BC(平行于同一条直线的两条直线互相平行)例2.已知∠DAC=∠ACB,∠D+∠DFE=1800,求证:EF//BC 平行线的判定两直线平行条件结论同位角相等内错角相等同旁内角互补条件同位角相等内错角相等同旁内角互补结论两直线平行夹在两平行线间的垂线段的长度,叫做两平行线间的距离。平行线的性质 ABCDE1F24、操作与解释：数学课上有这样一道题：“如图，以点B为顶点,射线BC为一边，利用尺规作∠EBC，使得∠EBC=∠A，EB与AD一定平行吗？”。小王说“一定平行”；而小李说“不一定平行”。你更赞同谁的观点？ 5、探索与思考：有一条直的等宽纸带，按如图所示折叠时，∠1=30°求纸带重叠部分中∠CAB的度数。ABC1234EF 已知：AB∥CD。试探索①∠A、∠C与∠AEC之间的关系；②∠B、∠D与∠BFD之间的关系。ABCDEF几何之旅1234l 证明：由：∠1+∠2=180°(已知)4123ABCEFD(同旁内角互补，两直线平行)∠1=∠3（对顶角相等)∠2=∠4（对顶角相等)所以∠3+∠4=180°(等量代换)AB//CD.例1.如图已知：∠1+∠2=180°，求证：AB∥CD。 ∵EF⊥AB，CD⊥AB（已知）∴EF//CD(垂直于同一条直线的两条直线互相平行)∴∠EFB＝∠DCB（两直线平行，同位角相等）∵∠EFB=∠GDC（已知）∴∠DCB=∠GDC（等量代换）∴DG∥BC（内错角相等,两直线平行）∴∠AGD=∠ACB（两直线平行，同位角相等）证明：例3.已知EF⊥AB，CD⊥AB，∠EFB=∠GDC，求证：∠AGD=∠ACB。 如图，两平面镜а、β的夹角为θ，入射光线AO平行于β入射到а上，经两次反射后的反射光线O"B平行于а，且∠1=∠2，∠3=∠4，则角θ=_____度аβθOBA12345例4.两块平面镜的夹角应为多少度?分析:由题意有OA//β,O"B∥a且∠1=∠2，∠3=∠4，由OA//β,∠1=∠θO‘B∥a,∠4=∠θ,∠2=∠5所以∠3=∠4=∠5=∠θ因为∠3+∠4+∠5=180°所以∠3=60°即θ=60° 1.命题的概念:判断一件事情的句子，叫做命题。命题必须是一个完整的句子;这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。2.命题的组成:每个命题是由题设、结论两部分组成。题设是已知事项;结论是由已知事项推出的事项。命题常写成“如果……，那么……”的形式。或“若……，则……”等形式。真命题和假命题:命题是一个判断,这个判断可能是正确的,也可以是错误的。由此可以把命题分成真命题和假命题。真命题就是:如果题设成立,那么结论一定成立的命题。假命题就是:如果题设成立时,不能保证结论总是成立的命题。命题 画线段AB=2cm直角都相等;两条直线相交，有几个交点?如果两个角不相等，那么这两个角不是对顶角。相等的角都是直角;分析:因为(1)、(3)不是对某一件事作出判断的句子，所以(1)、(3)不是命题。解.(1)、(3)不是命题;(2)、(4)、(5)是命题;(2)、(4)都是真命，(5)是假命题。例1.判断下列语句，是不是命题，如果是命题，是真命题，还是假命题? ABCD分析:不妨选择(1)与(2)作条件，由平行性质“两直线平行，同旁内角互补”可得∠A=∠C，故满足要求。由(1)与(3)也能得出(2)成立，由(2)与(3)也能得出(1)成立。解:如果在四边形ABCD中，AB//DC、AD//BC，那么∠A=∠C。例2.如图给出下列论断:(1)AB//CD(2)AD//BC(3)∠A=∠C以上，其中两个作为题设，另一个作为结论，用“如果……，那么……”的形式，写出一个你认为正确的命题。 课堂练习1、下列命题是真命题的有（）A、相等的角是对顶角B、不是对顶角的角不相等C、对顶角必相等D、有公共顶点的角是对顶角E、邻补角的和一定是180度F、互补的两个角一定是邻补角G、两条直线相交,只要其中一个角的大小确定了那么另外三个角的大小就确定了C、E、G 1.平移变换的定义:把一个图形整体沿某一方向移动,会得到一个新图形，这样的图形运动，叫做平移变换，简称平移。平移的特征:(1)平移不改变图形的形状和大小。(2)新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点，对应点连结而成的线段平行且相等。决定平移的因素是平移的方向和距离。经过平移，图形上的每一点都沿同一方向移动相同的距离。经过平移，对应角相等;对应线段平行且相等;对应点所连的线段平行且相等。平移 站在运动着的电梯上的人左右推动的推拉窗扇小李荡秋千运动躺在火车上睡觉的旅客分析:A、B、D属平移，在一个位置取两点连成一条线，在另一个位置再观察这条线段，发现是平行的，而C同样取两点连成一条线段，运动到另一位置时，可能已不平行解:选C例1.在以下生活现象中,不是平移现象的是 例2.如图所示,△ABC平移到△A′B′C′的位置,则点A的对应点是____,点B的对应点是____，点C的对应点是____。线段AB的对应线段是___________，线段BC的对应线段是______，线段AC的对应线段是_______。∠BAC的对应角是________，∠ABC的对应角是_________，∠ACB的对应角是_________。△ABC的平移方向是________________________________________，平移距离是_____________________________________________。ABCA′B′C′A′B′C′沿着射线AA′(或BB′，或CC′)的方向线段AA′的长(或线段BB′的长或线段CC′的长填空题 2.下列生活中的物体的运动情况可以看成平移的是()（1）摆动的钟摆（2）在笔直的公路上行驶的汽车（3）随风摆动的旗帜（4）摇动的大绳（5）汽车玻璃上雨刷的运动（6）从楼梯自由落下的球（球不旋转） 小结：1、邻补角、对顶角的概念和性质2、垂线画法、垂线段的性质3、平行线的判定和性质4、命题的题设与结论以及命题的真假5、平移的概念和平移的性质 如图，已知∠1=∠2，直线AC、BE交于B,∠A+∠C=1800,求证：AF//BE证明：∵∠1=∠2（已知）∴BE//CD(内错角相等,两直线平行)又∵∠A+∠C=1800（已知）∴AF//CD(同旁内角互补,两直线平行)∴AF//BE(平行于同一条直线的两条直线互相平行)DABCEF１2 如图，平行线AB、CD被直线AE所截，已知∠1=110o，则∠2、∠3、∠4分别是多少度？为什么？答：∠2=110o，因为两直线平行，内错角相等，∠2=∠1∠3=110o，因为两直线平行，同位角相等，∠3=∠1∠4=180o－110o=70o，因为两直线平行，同旁内角互补。（（（（4321DCBAE 如图，已知：AD∥BC,∠AEF=∠B,求证：AD∥EF。证明：∵AD∥BC（已知）∴∠A+∠B＝180°（两直线平行，同旁内角互补）∵∠AEF=∠B（已知）∴∠A＋∠AEF＝180°（等量代换）∴AD∥EF（同旁内角互补，两条直线平行） 例2：如图，已知：AE平分∠BAC，CE平分∠ACD，且AB∥CD。求证：∠1＋∠2=90°证明：∵AB∥CD（已知）∴∠BAC＋∠ACD=180°(两条直线平行，同旁内角互补)又∵AE平分∠BAC，CE平分∠ACD（已知）∴∠1＝∠BAC,∠2＝∠ACD（角平分线的定义）∴∠1+∠2＝(∠BAC＋∠ACD)（等式的性质）＝×1800＝900即∠1＋∠2=900 例5：如图，已知：AB∥CD，∠A＝∠C，求证：AD∥BC。证明：∵AB∥CD（已知）∴∠A＋∠D=180°(两条直线平行，同旁内角互补)∵∠A＝∠C（已知）∴∠C＋∠D=180°（等量代换）∴AD∥BC（同旁内角互补，两条直线平行） 如图2-73。已知：∠1=∠2，AC平分∠DAB，求证：AB∥CD。1 8.如图，已知：AC∥DE，∠1=∠2，试证明AB∥CD.证明：∵由AC∥DE（已知）∴∠ACD=∠2(两直线平行，内错角相等)∵∠1=∠2（已知）∴∠1=∠ACD(等量代换)∴AB∥CD(内错角相等，两直线平行)ADBE12C 巩固提高3.如图所示，∠1=∠2，∠BAC=20°，∠ACF=80°.（1）求∠2的度数；（2）FC与AD平行吗？为什么？ 巩固提高4.如图所示，已知∠1=∠2，∠3+∠4=180°,则a与c平行吗？为什么？ 巩固提高5.如图所示，如果∠1=47°，∠2=133°，∠D=47°，那么BC与DE平行吗？AB与CD平行吗？ 巩固提高6.如图所示，已知∠D=∠A，∠B=∠FCB，试问ED与CF平行吗？ 巩固提高7.已知,如图，点B在AC上，BD⊥BE，∠1+∠C=90°，问射线CF与BD平行吗？试用两种方法说明理由. 如图，∠BHE与∠BGF互为补角，∠D=∠A．求证：∠B=∠C．综合应用⑴观察图形中的∠B与∠C具有怎样的位置关系？⑵AB与CD具有怎样的位置关系时，才能说明∠B=∠C？⑶由已知条件能说明AB与CD平行吗？问题分析： 如图，∠BHE与∠BGF互为补角，∠D=∠A．求证：∠B=∠C．综合应用解：因为∠BHE+∠BGF=180°,所以∠BGF=∠BHA（同角的补角相等）,所以AE//DF(同位角相等，两直线平行）,∠BHE+∠BHA=180°,所以∠A=∠BFD(两直线平行，同位角相等).又因为∠D=∠A，所以∠BFD=∠D,所以AB//CD（内错角相等，两直线平行）.所以∠B=∠C（两直线平行，内错角相等）. 如图所示，是汽车灯的灯碗的纵切面，从位于O点的灯泡发出的两束光线OB和OC经过灯碗反射后,沿BA和CD方向平行射出，如果∠ABO=46°,∠DCO=48°，求∠BOC．综合应用思路点拨：构造BA和CD的平行线OE,从而构造出平行线间夹的两对内错角.EOCBDA 祝同学们学习进步再见 半命题作文中考作文考前辅导之 半命题作文：命题者只提供一个不完整的题目,由学生将题目残缺的部分补充完整后再进行写作的一种作文样式。定义 考一考你的观察力（一）__________________，我开心地笑了（二）幸福的感觉其实很多：求知是一种幸福，给予是一种幸福；亲近自然是一种幸福，回报社会是一种幸福；享受成功是一种幸福，历经磨炼是一种幸福……请以“  ___________是一种幸福”为题，写一篇文章。（三）为了迎接春天，小草在孕育新绿；为了迎接风雨，雏鹰在磨砺羽翼；为了迎接挑战，你在挥洒汗水……朝着一个目标而努力的生活总是充实的，因为在这些日子里，有太多期盼、太多付出、太多感受、太多故事……请以“在迎接________________的日子里”为题，在横线上填写适当的词或短语，把题目补充完整，写一篇文章。（四）请以“我心中的那__________（一轮太阳、一抹绿色、一份天真、一丝牵挂……）为题写一篇文章。出题形式：（1）直接填空型（2）给出导语型（3）给出备选词语型 标题，是文章内容的高度浓缩；标题，是文章的眼睛，透过它可以洞悉文章的灵魂。常言道，题好一半文。从某种程度上说，拟题的优劣直接关系到文章品位的高低。写好半命题作文的关键在补题。而拟一个恰当的标题首先要审清题意。 半命题作文拟题常出现的问题？《挫折也美丽》：8人《失败也美丽》：7人拟题雷同《生活也美丽》《板书也美丽》拟题宽泛拟题随意《——也美丽》 限制部分命题作文开放部分材料作文《——也美丽》半命题作文的特点 《————也美丽》美丽？景题意也主语人事真美丽也最美丽 “也”如何体现？小草溪流平凡白发挫折失败鲜花大海伟大青丝顺利成功要有参照物审题完成了吗？ 审题仅仅为了补题吗？确定文章的立意——歌颂美丽确定文章题材——真实确定写作重点——美丽的原因明确文章体裁——记叙文明确其他要求(字数等） 判断下列补题及开头、结尾是否准确把握题意了？ 开头：学生作文1——《冬雪也美丽》在我的心中，最美的季节是冬天，最美的景物便是唯有在冬天才会有的——雪。每当下雪的时候，我都会跑到门外，欣赏那洁白的雪花，心情也会好起来。写的不是“也”美丽，而是“最”美丽。学生作文2——《失败也美丽》失败，是每个人都会经历的。有的人讨厌它，一味躲避，这样只能离它更近；而有的人在失败之后，从中吸取教训，不断努力，慢慢走向了成功。对于这些人，失败是美丽的。写的不是“也”美丽的，而是“是”美丽的。学生作文3——《配角也美丽》有人说，主角永远是舞台上最耀眼、最美丽的那轮明月，而配角只是旁边点缀的小星，黯然无光。可在我看来，其实，配角和主角一样，也很美丽。 如何体现“也美丽”？比较三个结尾。《皱纹也美丽》我的目光久久停留在那皱纹上，此时我突然感觉到父亲眼角的皱纹是如此美丽，它里面包含了父亲对我深深的爱。我很庆幸我拥有这样的父亲。《旧毛手套也美丽》这双手套我一直珍藏到现在，它虽然不好看，但在我心中永远是最美的。《失败也美丽》成功固然美丽，但失败是成功之母，没有一次次的失败，怎能得到一个个通向成功的阶梯呢？当你从失败中吸取教训、不断总结、不断努力而最终成功的时候，你会突然发现：原来失败也是美丽的。美丽父亲对我深深的爱最美失败也是美丽的结尾揭示美丽的“内涵”，并且对比“成功”而言，扣题。也?也?美丽? 审题练习1题目：《我尝到了——的滋味》偏正短语，修饰中心词“滋味”的，应是酸、甜、苦、辣、咸之类的表示滋味感受的词语。再考虑，所补充的内容应该是表现思想感受的词，如痛苦、幸福、喜悦、沮丧等。注意：尝到的滋味对你有什么启示和影响一定要写出来。 审题练习2请以《从此，我不再》为题，写一篇不少于600字的记叙文。提示：先把题目补充完整，然后作文。横线上可填的词语如：任性、自卑、孤独、偷懒、害怕困难、迷恋网络、受人关注、拥有笑容……填写谓语（根据自己的生活经历填写）从此——重点内容不再——有铺垫，有对比'