最新邻里中心模式及案例分析课件PPT.ppt 69页

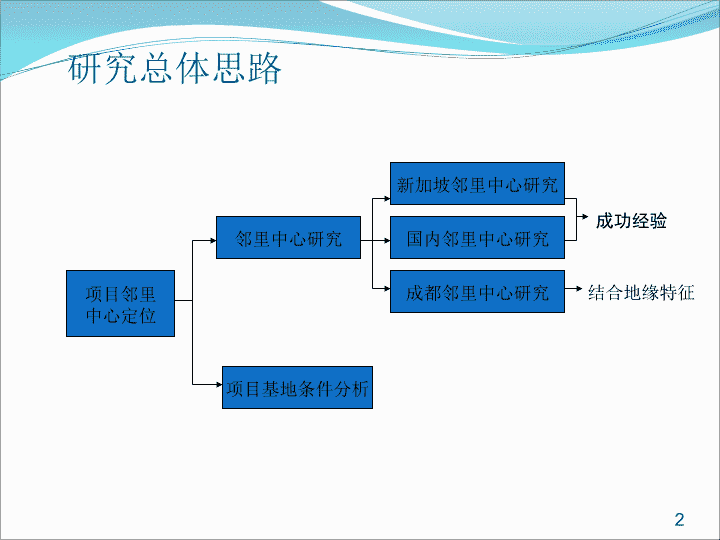
'邻里中心模式及案例分析 项目邻里中心定位邻里中心研究项目基地条件分析新加坡邻里中心研究国内邻里中心研究成都邻里中心研究结合地缘特征成功经验研究总体思路2 第一部分邻里中心研究3 新加坡邻里中心研究3商业分级新镇中心邻里中心邻区商店配置标准40000—60000套住户，1.27m2对1单位组屋配置6000—8000套住户,按1.27m2对1单位组屋配置1000—1200套住户，按1.27m2对1单位组屋配置商品档次高档商品中档商品生活必须品必备功能娱乐设施、银行、邮政局、超级市场、百货公司及高档商品、商店、餐馆、快餐店诊疗所及牙医、面包店、文具店、中西药行、托儿所、服装店、眼镜店、理发店、家庭用品、书局、家庭娱乐中心。典型的邻里中心包含35个商店、2个食阁、1个超级市场、1个菜市场、1—2台自动提款机。普通日用商店和餐厅7 中国邻里中心研究1中国邻里中心发展历程及发展趋势发源：中国的邻里中心是在借鉴新加坡公共管理先进理念的基础上，由苏州工业园区率先引入国内。苏州工业园区结合自身园区商业开发，并通过多年实践已摸索出一整套适合中国国情的商业地产开发运营管理模式，苏州工业园区邻里中心也成为了集商业、文化、体育、卫生、教育于一体的区域性商业服务中心。“邻里中心”也成为了中国第一个社区商业服务的品牌商标，其品牌及软件已面向全国输出。现状：国内很多类似于邻里中心（社区商业）的业态是不成规模、不成气候的，服务也不完整，物业类型以商业街为主，没有一个完整的配置概念。由于苏州工业园邻里中心的成功运营，国内部分特大城市已将邻里中心纳入城市规划，如上海不做市区十字路口经济，将提升和创新郊区“邻里中心”商业发展模式，以此推动上海的国际化和城市化进程；南京河西新区的规划中，已在每个街道规划了一个“邻里中心”。发展趋势：邻里中心将被国家纳入城市规划，扮演区域基础商业角色。8 中国邻里中心典型案例一——苏州工业园区1邻里中心是苏州工业园区在第三产业和公益事业及其经营管理方面借鉴新加坡经验而创造的一种新颖的社区服务形态，也是国内最早最成功的邻里中心。苏州工业园的邻里中心以全方位、多功能、各层次的综合性社区商业服务业为发展主线，并按照邻里中心规划先行原则，在园区内规划了17个邻里中心，目前已成功运营了四个综合性商业服务中心：邻里中心湖东大厦、邻里中心新城大厦、邻里中心贵都大厦和邻里中心师惠大厦。师惠大厦贵都大厦湖东大厦9 中国邻里中心典型案例一——苏州工业园区2服务理念：以12项必备功能为基础，让顾客满意、经营者满意、政府满意“三满意”，服务内涵是综合性、全方位、多功能、各层次。物业形态：综合型大厦，层数大多为四层（新城大厦及贵都大厦）。配置标准：按２万人组团配置一个邻里中心标准规划，2万人组团一般有5、6个住宅小区，辐射直径为0.5-1.5公里，面积按1000-1500m2/千人配置。业态定位：80%以服务业为主，其中40%-50%为餐饮业。12项必备功能为银行、超市、邮政、餐饮店、洗衣房、美容美发店、药店、文化用品店、维修点、社区活动中心、净菜场、卫生所。运营管理：功能定位在先，招商紧随其后，再将单纯的物业管理跨越到“现场管理加物业管理”。销售模式：三权分离，承诺投资回报的产权式商铺销售模式。招商政策：主要针对品牌连锁商家。开发成本加物业费的低租金吸引经营者。10 中国邻里中心典型案例一——苏州工业园区3四大邻里中心比较研究楼盘名新城大厦贵都大厦师惠大厦湖东大厦总建筑面积21600m211000m212300m230000m2服务人口2万人层数4层4层特色业种健身俱乐部、小吃街3-4F为写字楼邻里假日酒店、新型菜场、特色餐饮家电零售、家装配套、汽车展销、7000m2美食大楼、2500m2菜场；商业、金融和中介服务三条街停车场6000m23500m211 中国邻里中心典型案例二——上海联洋社区1上海联洋社区总建筑面积250万m2，社区配套服务面积为30万m2，其中商业面积占10万m2。联洋邻里中心设有大型综合商业中心（SHOPPINGMALL），占地50920m2，总建筑面积71300m2。12 中国邻里中心典型案例二——上海联洋社区2物业形态：街区商业及综合型大厦，层数三层。配置标准：面积按1400m2/千人配置。业态定位：以核心SHOPPINGMALl为中心，主力店有联华生鲜超市、4000m2意大利商品展示中心、1.7万m2LAYA俱乐部及1300m2室内溜冰馆。招商优惠政策：由于租赁情况不佳，推出了局部两年免租等极大的优惠条件经营情况：较为冷清，还有近2/3的商业面积未租赁。失败原因：规划失败：商业的通道及进出口设计不合理，通道宽度太窄（仅5米），自行车库规划位置不合理，阻碍行人通行。开发进度失败：联洋社区邻里中心开发时间超前于住宅开发进度，造成了大面积空置现象。商业的开发进度应随整体住宅项目的开发进度及入住人口的实际情况适时控制。13 成都邻里中心研究成都目前还没有真正的邻里中心，类似于邻里中心的社区基础商业主要分布于以下几种物业：街区商业：规划条件限制了开发商在开发住宅用地时必须有商业配套，以此来保证居民的基本生活。街区商业有着易分割、独立性强、自主性强、易管理、易销售等优势，已成为了开发商追求盈利及资金迅速回笼的最常用的商业开发模式，也是成都最主要的基础商业的物业形态。由于商业街大多缺乏统一管理及规划，业主自主性强，导致了成都的基础商业配置不齐全，且十分零散局面。会所：是小区居民交流、活动、休闲的社区公共场所，以方便业主为出发点，是社区基础配套之一，由于规模及服务人口的限制，无法为小区居民提供完整的社区服务，有60%以上会所目前处于亏损状态。14 成都邻里中心典型案例一——罗马假日广场罗马假日广场位于成都市一环路南段与高升桥东路交汇处。该商业物业是成都市最早推出的邻里购物中心，一经推出，便火爆发售。但是，由于街区划分的短视，虽然好又多有旺盛的人流，但临街的商铺却不能很好地利用这一资源，使得现有的商铺经营状况惨淡。15 成都邻里中心典型案例二——玉林生活广场玉林生活广场是集餐饮、娱乐、休闲、购物与办公为一体的欧式风情的超大街区式邻里型购物中心。在开发之时，玉林生活广场定位是玉林社区唯一的一个高档次邻里型购物中心概念，改变传统的小门面经营模式，服务社区邻里生活。但实际的情况确是成为餐饮娱乐的强势口岸。16 对本案邻里中心的启发核心优势：邻里中心是一个区域或组团的基础商业，解决了新兴住区基础配套的难题，优化了住区与商业矛盾，还能带动地价的迅速攀升。配置标准：邻里中心大多按人口配置，通常按6000-8000户或2万人组团配置一个邻里中心，沿海城市的邻里中心面积配置标准为1000-1500m2/千人，由于成都经济、人均收入及消费均不及沿海城市，成都的面积配置标准应在此基础上略微降低，建议按850m2/千人配置,辐射直径为0.5-1.5公里。物业形态：综合型大厦或内街外廊建筑，层数不超过四层，应注重人流导入及交通动线规划。功能定位：应结合商业、文化、体育、卫生、教育于一体，并以80%服务业为主（其中40-50%为餐饮业）。开发进度：应随整体住宅项目的开发进度及入住人口的实际情况适时控制，避免出现上海联洋社区邻里中心大面积空置现象。17 对本案邻里中心的启发邻里中心必备功能：18 对本案邻里中心的启发运营模式：已突破原有初始阶段的社区服务模式，上升到了一种以房屋租售为经营基础、以市场需求作功能定位、由房东身份进行行业管理的区域性、综合型商业服务新业态。以三权分离为核心，导入功能定位及城市规划理念，招商紧随其后，再将单纯的物业管理跨越到“现场管理加物业管理”。招商模式：主要针对品牌连锁商家。以低租金及优惠招商政策吸引商家。销售模式：结合成都地缘特征，建议本案邻里中心可以采用包租（承诺投资回报）+旗舰带动型的销售模式。19 第二部分项目邻里中心定位20 项目邻里中心开发目的成为住区基本配套，以满足社区居民日常生活为主提升住区品质，解决居住环境与商业的矛盾将本案的商业做强，让商业价值最大化21 项目邻里中心区位邻里中心邻里中心22 项目邻里中心控规邻里中心邻里中心用地性质：公共服务设施用地用地面积：4264容积率：1.8限高：24米密度：35%绿化率：30%LTF：社区服务中心、公厕用地性质：公共服务设施用地用地面积：3978容积率：1.8限高：24米密度：35%绿化率：30%LTF：社区服务中心、公厕用地性质：农贸市场用地面积：3167容积率：2.0限高：24米密度：45%绿化率：20%用地性质：农贸市场用地面积：3296容积率：2.0限高：24米密度：45%绿化率：20%23 项目邻里中心商圈范围定位核心商圈：以服务本案住区为主，辐射范围约0.5公里以内，服务人口约2.5万人。次级商圈：以服务区域住区居民为主，特别以高新西区居民为主，辐射范围为1公里以内，服务人口约3万人。24 项目邻里中心规模定位地块可实现的最大规模：27761.6m2（按最大容积率计算）市场需求规模：沿海城市的邻里中心面积配置标准为1000-1500m2/千人，由于成都经济、人均收入及消费均不及沿海城市，成都的面积配置标准应在此基础上略微降低，建议按850m2/千人配置，本区域内居住人口按三万人计算，邻里中心面积应在2.55万平米左右。25 项目邻里中心业态定位1社区商业基本业态购物服饰、家具店、家居饰品店、装饰材料店、灯具店、五金店、水族用品店、花店等休闲娱乐KTV、网吧、健身房、咖啡店、茶楼、水吧、酒吧、洗浴中心、保健中心等餐饮特色餐饮店（如咖哩专卖），快餐店（面馆，品牌快餐），连锁早餐店、名小吃店（龙抄手、钟水饺）等社区服务美容美发店，配钥匙、装琐、刻印，汽车美容店，租车行，各种培训中心（如计算机培训中心），外语教学处，牙科诊所，中医诊所，药店，彩扩店，干洗店，音像租赁店，水电维修，打字、复印店等26 项目邻里中心业态定位2邻里中心12项必备基本功能27 项目邻里中心业态定位3档次定位：中档商品为主。本案邻里中心业态定位（以12项必备功能为核心）主营业态经营内容规模品牌商家超市副食品、日杂用品1000-2000㎡新一佳、红旗、互惠等菜市场蔬菜、肉类、禽蛋、水产，粮油、干货、水果、冷冻食品1500-2000㎡医疗卫生诊所、中西药店、牙医100-200㎡同仁堂、德仁堂、唐牙科等银行银行1-3家或提款机2个200-300㎡建行、中国银行、工行等文化用品书店、文具用品店、音像制品店（VCD租赁店）150-200㎡新华书店、文轩书店等28 项目邻里中心业态定位4主营业态经营内容规模品牌商家邮政快递、汇款、包裹、信件、鲜花等50-100m2中国邮政、宅急送等维修店换锁、配钥匙、刻印、鞋子修理店、家居维修店等10-50㎡5-10维修店等洗衣房清洁、熨汤及服饰修改100-200㎡4-8家，美国布兰奇等美容美发美发、美容美体SPA店、减肥中心50-500㎡流行前线、佐登妮丝、箩娅蒂丝纤丝鸟减肥纤体中心等社区活动中心棋牌室、老年活动中心、培训班（儿童语数外培训、成人外语培训、网球培训、老年培训中心等）1000㎡——29 项目邻里中心业态定位5主营业态经营内容规模品牌商家餐饮早餐店、小吃店、快餐店、特色餐饮30-1000m2必胜客、肯德基、麦当劳、德克士、龙抄手、钟水饺、叶抄手、巴西烤肉、日本料理等休闲娱乐KTV量贩、网吧、健身房、咖啡店、茶楼、水吧、酒吧、洗浴中心、保健中心等100-1000㎡吸引力、浩沙健身俱乐部、良木缘咖啡、半打啤酒馆、何日君、富侨保健等生活服务鲜花礼品、摄像彩扩店、西点店、日用杂品店10-50㎡特百惠、科达、玛萨面包等家居配套家居饰品店、装饰材料店、灯具店、五金店、水族用品店、30-100㎡10-20家。30 项目邻里中心产品形态定位物业形态：建议以内街外廊的建筑为主。层数：局部四层空间设计原则：商业空间的步行化、休闲化、个性化、在有限空间的利益最大化。旗舰店带动原则：注重超市及新型菜场等主力店规划，着重依托主力店带动邻里中心整体人气及商气。内部交通动线设计：着重通过庭院式景观节点对内部人流的有效导向。31 谢谢！32 第三章工业机器人运动学 引言要实现对工业机器人在空间运动轨迹的控制，完成预定的作业任务，就必须知道机器人在空间瞬时的位置与姿态。如何计算机器人手部在空间的位姿是实现对机器人的控制首先要解决的问题。本章讨论机器人运动学的基本问题，将引入齐次坐标变换。推导出坐标变换方程；利用DH参数法，进行机器人的位姿分析；介绍机器人正向和逆运动学的基础知识。 主要内容数学基础——齐次坐标变换机器人运动学方程的建立（正运动学）机器人逆运动学分析 一、机器人数学基础——齐次坐标变换1.1引言1.2点向量和平面的描述1.3变换1.4平移变换1.5旋转变换1.6坐标系1.7相对变换1.8物体的描述1.9逆变换1.10一般性旋转变换1.11等价旋转角与旋转轴1.12扩展与缩小1.13透视变换1.14变换方程1.15小结 1.1引言(Introduction)机器人操作涉及到各物体之间的关系和各物体与机械手之间的关系。这一章将给出描述这些关系必须的表达方法。类似这种表示方法在计算机图形学中已经解决。在计算机图形学和计算机视觉中，物体之间的关系是用齐次坐标变换来描述的。在本课程我们将采用齐次坐标变换来描述机械手各关节坐标之间、各物体之间以及各物体与机械手之间的关系。本章首先介绍向量和平面的表示方法，然后引出向量和平面的坐标变换，这些变换基本上是由平移和旋转组成，因此可以用坐标系来描述各种物体和机械手的空间位置和姿态。稍后还要介绍逆变换，逆变换是运动学求解的基础。 a0vzyxzyxpcb0uEH图1.1点向量的描述•1.2点向量和平面的描述（Notationofpointvectorsandplanes）1.2.1点向量（Pointvectors）点向量描述空间的一个点在某个坐标系的空间位置。同一个点在不同坐标系的描述及位置向量的值也不同。如图1.1中，点p在E坐标系上表示为Ev，在H坐标系上表示为Hu，且v≠u。一个点向量可表示为v=ai+bj+ck通常用一个（n+1）维列矩阵表示，即除x、y、z三个方向上的分量外，再加一个比例因子w，即v=[xyzw]T其中a=x/w,b=y/w,c=z/w。改变比例因子w，则分量a、b、c的数值相应改变，但描述的还是同一个点向量。如v=3i+4j+5k可表示为v=[3451]T=[68102]T=[-3-4-5-1]T在向量中增加一个比例因子w是为了方便坐标变换中的矩阵运算。 已知两个向量a=axi+ayj+azkb=bxi+byj+bzk（1.1）向量的点积是标量。用“·”来定义向量点积，即a·b=axbx+ayby+azbz（1.2）向量的叉积是一个垂直于由叉积的两个向量构成的平面的向量。用“×”表示叉积，即a×b=(aybz¯azby)i+(azbx¯axbz)j+(axby¯ayby)k（1.3）可用行列式表示为ijka×b=axayaz（1.4）bxbybz 1.2.2平面（Planes）平面可用一个行矩阵表示，即p=[abcd]（1.5）它表示了平面p的法线方向，且距坐标原点的距离为－d/m，其中m=（1.6）如图1.2所示，如果将x－y平面沿z轴正方向平移一个单位距离，构成平面p，则p=[001-1]即a=0,b=0,c=1,d=-1,m==1平面p上任一点v为v=[xy11]T，它与平面p的点乘为零，即p•v=0平面p上方任一点v，如v=[0021]T，它与平面p的点乘为一个正数，即p•v=1平面p下方任一点v，如v=[0001]T，它与平面p的点乘为一个负数，即p•v=-1注意：平面[0000]无定义。a2+b2+c2a2+b2+c2图1.2平面的描述0•vpzyx1yx H空间的变换是由4×4矩阵来完成的，它可以表示平移、旋转、扩展和透视等各种变换。如已知点u（在平面p上）,它的变换v（在平面q上）用矩阵积表示为v=Hu（1.7）其中H为4×4变换矩阵，u和v为4×1的点列向量，相应的平面p到q的变换是q=pH-1（1.8）其中H-1为H的逆阵，p和q为1×4的平面行向量。经变换后的平面向量q与点向量v的点乘为q·v=pH-1·Hu＝p·u（1.9）与变换前平面p与点u的点乘相等，证明了变换的等效性。1.3变换(Transformation) 1.4平移变换（Translationtransformation）用向量h＝ai+bj+ck进行平移，其相应的H变换矩阵是100a010bH=Trans(abc)=001c(1.10)0001因此对向量u=[xyzw]T，经H变换为向量v可表示为x+awx/w+ay+bwy/w+bv=z+cw=z/w+c(1.11)w1可见，平移实际上是对已知向量u=[xyzw]T与平移向量h=[abc1]T相加。 【例1.1】对点向量u=[2321]T进行平移，平移向量为h=[4-371]T，则平移后的向量为v=[6091]T，或100426010―330v=H∙u=00172=9000111点向量的平移过程如图1.3所示。对平面的平移则用H－1进行变换，如对平面p=[100-2]进行H变换为平面q，则根据变换原理有100-40103q＝pH－1＝[100-2]001-70001＝[100-6]平面p＝[100-2]是y－z平面沿x正方向移动2个单位形成的平面（图1.3），点u=[2321]T是平面p上的一个点，它们的点乘p∙u=0。经H变换后的平面q＝[100-6]是y－z平面沿x正方向移动6个单位形成的平面，点v=[6091]T是平面q上一个点，平面q与点v的点乘也应是零，即q∙v＝0，说明变换前后的结果不变，证明H变换是正确的。u•0zyx3P22图1.3点向量的平移•v69qp 1.5旋转变换（Rotationtransformation）如图1.4所示，绕x,y,z轴旋转一个θ角的相应变换是10000cosθ-sinθ0Rot(x,θ)=0sinθcosθ0（1.12）0001cosθ0sinθ00100Rot(y,θ)=-sinθ0cosθ0(1.13)0001cosθ-sinθ00sinθcosθ00Rot(z,θ)=0010(1.14)0001注意：θ角旋转的正方向遵循右手螺旋法则（如图1.4所示）图1.4旋转变换θ0zyxθθ 【例1.2】点u=7i+3j+2k，它绕z轴旋转90°为v，经式（1.14）变换得到（sinθ=1，cosθ=0）0-1007-3100037v=Rot(z,90°)=00102＝2000111起始点u和终点v如图1.5所示。如将v点再绕y轴旋转90°得到w。用式（1.13）变换得到0010-32010077w=Rot(y,90°)=-10002＝3000111结果如图1.6所示。如果将上述两次旋转结合起来，写成一个表达式得到w=Rot(y,90°)v＝Rot(y,90°)Rot(z,90°)u用两个变换矩阵Rot(y,90°)、Rot(z,90°)和起始点u代入上式计算的结果与前面分两次计算的结果相同。2•uzyx•v0图1.5Rot(z,90°)yuv0zx•w••图1.6Rot(y,90°)Rot(z,90°)27 为此，先将点u绕z轴旋转90°，然后再绕y轴旋转90°，我们得到00100-100720100100037w＝Rot(y,90°)Rot(z,90°)u=-100000102＝30001000111如果按着逆序旋转，首先绕y轴旋转90°，然后再绕z轴旋转90°，其结果为0-10000107-31000010032w=Rot(z,90°)Rot(y,90°)u=0100-10002=-70001000111逆序旋转的结果如图1.7所示。显然，变换的顺序不同，其结果也不同。这从矩阵相乘是不可交换的（AB≠BA）也可以得到证明。 如对经过两次旋转变换得到的点向量w再进行一次平移（平移向量为h＝[4-371]T），则可得到如图1.8所示的点向量n。变换过程如下100426010-374n=Trans(4,－3,7)w=00173=10000111zuv0yx•w••图1.8Trans(4,-3,7)Rot(y,90°)Rot(z,90°)•••n72w0zyx•••u图1.7Rot(z,90°)Rot(y,90°)2-7v 1.6坐标系(Coordinateframes)齐次变换矩阵H由四个列向量组成，它的前三个列向量称为方向向量，由式（1.12）到式（1.14）的旋转变换（分别绕x、y、z轴旋转θ角）确定，第四个列向量称为平移向量，它的平移分量（沿x、y、z轴的平移量）由式（1.10）第四列的前三个元素确定。如0014100-3H＝Trans(4,-3,7)Rot(y,90°)Rot(z,90°)=0107（1.15）0001坐标系的原点，即零向量[0001]T的H变换是[4-371]T，相当于将原点按平移向量的各个分量进行平移的结果（如图1.9所示）。如果对x、y、z轴的单位向量进行H变换，分别得到[4-271]T、[4-381]T和[5-371]T。这四个向量在图1.9中标出，并形成了一个新坐标系。0zyxzyx0Trans(4,-3,7)Rot(z,90°)Rot(y,90°)图1.9坐标原点与单位向量的H变换 这个新坐标系的x、y、z轴的方向分别是[0，1，0，0]T、[0，0，1，0]T和[1，0，0，0]T，它是由单位向量的H变换减去这个坐标原点的向量得到的。这些方向向量相应于变换矩阵的前三列（见式（1.15））。可见，H变换矩阵描述了一个坐标系绕原参考坐标系旋转和对参考坐标系平移的三个轴的方向和原点的位置（见图1.9）。如图1.10所示，当对一个向量n进行式（1.15）给出的H变换时，原向量n可以被认为是在新坐标系描述的那个向量u，即被变换了的向量u就是相对于参考坐标系描述的同一个向量n。00zzyyxxu(7,3,2,1)•n(6,4,10,1)图1.10向量的H变换 1.7相对变换（Relativetransformation）我们刚刚描述的旋转和平移都是相对于一个固定的坐标系而进行的。这样，在已给的例子里0014100-3Trans(4,-3,7)Rot(y,90°)Rot(z,90°)=0107（1.16）0001坐标系首先绕参考坐标系z轴旋转90°，然后绕y轴旋转90°，最后平移4i－3j+7k，如图2.9所示。如果以相反次序从左到右来进行这些操作：首先对坐标平移4i―3j+7k，然后将它绕当前坐标系的y轴旋转90°，此时当前坐标系的y轴与参考坐标系的y轴是相同的。然后再绕着新坐标系（当前的）坐标系的z轴旋转90°，所得结果与前面的方法相同（见图1.11）。 •00zzzzyyyyxxxxRot(y,90°)Rot(z,90°)Trans(4,-3,7)坐标原点图1.11相对变换 一般的情况下，如果我们用一个旋转和/或平移变换矩阵右乘一个坐标系的变换，那么产生的平移和/或旋转是相对于前一个变换的坐标系（当前坐标系）的轴来说的。如果我们用一个描述平移和/或旋转的变换矩阵左乘一个坐标系的变换，那么产生的平移和/或旋转是相对于基坐标系来说的。【例1.3】给一个坐标系C和一个变换T，T为绕z轴旋转90°，并在x轴方向上平移10个单位，当变换是相对于基坐标系产生时，我们用T左乘C得到新的位置x为0-1010100200010100000-11010020x=TC=00100100＝0100（1.17）000100010001当变换是相对于当前坐标系C轴产生时，我们用T右乘C得到新的位置y为100200-10100-103000-110100000-110y=CT=01000010＝1000（1.18）000100010001结果如图1.12所示。 YXTrans(10,0,0)Rot(z,90°)0zyxxxxxyyyyzzzzRot(z,90°)Trans(10,0,0)图1.12相对于基坐标系和当前坐标系的变换 1.8物体的描述（Objectrepresentation）变换可用来描述物体的位置与方向（方位）。如图1.13所示的楔形物体用六个角点来描述，这六个角点是相对于物体所在的参考坐标系的。如果把物体绕z轴旋转90°，然后绕y轴旋转90°，接着沿x方向平移4个单位，我们可以描述这个变换为00141000Trans(4,0,0)Rot(y,90°)Rot(z,90°)=01000001这个变换表示了对参考坐标系的旋转和平移操作，变换后物体的六个角点为44664400141-1-111-11-1-111-11000000044000044=01000002201111110001111111变换后该物体在坐标上的方位如图1.13所示。 从图1.13可以看出，由于楔形物体的角点与它所在的坐标系有固定的关系，因此没有必要对所有的角点进行变换，只要对物体所在的坐标系进行变换，就可得到变换后的各个角点在基坐标中的位置，将这些角点用直线连接起来就可得到楔形物体的边缘，它与逐点变换的结果完全相同（见图1.14）。(-1,0,0)(-1,0,2)(1,0,2)(1,4,0)(-1,4,0)(1,0,0)zyx0图1.13楔形物体图1.14被变换的楔形物体(4,1,0)(4,-1,4)(4,1,4)(6,1,0)(6,-1,0)(4,-1,0)yx0yxzz 1.9逆变换（Inversetransformation)所谓逆变换就是将被变换的坐标系返回到原来的坐标系，在数学上就是求变换矩阵的逆。下面我们写出变换矩阵的一般表达形式nxoxaxpxnyoyaypyT=nzozazpz（1.19）0001式中n,o,a是旋转变换列向量，p是平移向量，其逆是nxnynz-p.noxoyoz-p.oT-1=axayaz-p.a（1.20）0001式中的“.”表示向量的点积。这个结果很容易用式1.19右乘式1.20是单位矩阵来证明。 1.10一般性旋转变换（Generalrotationtransformation）前面我们介绍的旋转变换都是绕x，y，z轴旋转的旋转变换，这些变换都有一个简单的几何解释。例如：在绕z轴旋转的情况下，表示z轴保持恒定，x轴和y轴将如图1.15所示那样变化。图1.15绕z轴的旋转θz0zyyxxCosθ－SinθSinθCosθθ 如图1.16所示，给出一个变换矩阵C，它绕任意向量k旋转，我们把k当作C坐标系的z轴单位向量。nxoxax0nyoyay0C=nzozaz0（1.21）0001k=axi+ayj+azk（1.22）绕k旋转就相等于绕C坐标系的z轴旋转。Rot（k，θ）=Rot（Cz，θ）（1.23）如果我们给一个坐标系T，它在参考坐标系里被描述，它在C坐标系里用X描述，这样T=CX（1.24）其中X描述T相对C的位姿，求X，我们得到X=C-1T（1.25）kTzzyyxxx00图1.16一般性旋转变换C T绕k旋转就等于Ｘ绕Ｃ坐标系的z轴旋转Rot（k,θ）Ｔ＝CRot（z,θ）X（1.26）Rot（k,θ）Ｔ＝CRot（z,θ）C-1T（1.27）这样Rot（k,θ）＝CRot（z,θ）C-1（1.28）展开式（1.28），我们发现CRot（z,θ）C-1仅是k的函数。用C-1右乘Rot（z,θ），我们得到cosθ-sinθ0　0　　nxnynz0sinθcosθ00　　oxoyoz0Rot（z,θ）C-1＝　00　10　　axayaz00　　0　010001nxcosθ－oxsinθnycosθ―oysinθnzcosθ―ozsinθ0nxcosθ+oxsinθnycosθ+oysinθnzcosθ+ozsinθ0=axayaz0（1.29）0001再用C左乘nxoxax0nyoyay0C=nzozaz0（1.30）0001 得到CRot（z,θ）C-1=nxnxcosθ―nxoxsinθ+nxoxsinθ+oxoxcosθ+axaxnynxcosθ―nyoxsinθ+nxoysinθ+oyoxcosθ+ayaxnznxcosθ―nzoxsinθ+nxozsinθ+ozoxcosθ+azax0nxnycosθ―nxoysinθ+nyoxsinθ+oyoxcosθ+axaynynycosθ―nyoysinθ+nyoysinθ+oyoycosθ+ayaynznycosθ―nzoysinθ+nyozsinθ+oyozcosθ+azay0nxnzcosθ―nxozsinθ+nzoxsinθ+ozoxcosθ+axaz0nynzcosθ―nyozsinθ+nzoysinθ+ozoycosθ+ayaz0nznzcosθ―nzozsinθ+nzozsinθ+ozozcosθ+azaz0（1.31）01 应用下列关系进行简化：C坐标系任意的行或列与其他行或列的点积为零，因为这些向量是正交的；C坐标系任意的行或列与其自身的点积为I，因为它们是单位量；z向量是x和y向量的叉积：a=n×o，它有下列分量ax=nyoz―nzoyay=nzox―nxozaz=nxoy―nyox正矢Versθ=（1―cosθ），简写成Versθ，且kx=ax，ky=ay，kz=az。由此可得到简化式为Rot(k,θ)=kxkxVersθ+cosθkykxVersθ―kzsinθkzkxVersθ+kysinθ0kxkyVersθ+kzsinθkykyVersθ+cosθkzkyVersθ―kzxsinθ0kxkzVersθ―kysinθkykzVersθ+kxsinθkzkzVersθ+cosθ0（1.32）0                                   0                                  01上式是一般性的旋转变换的重要结论。从这个结论可以得出每一个基本旋转变换。例如：Rot(x,θ)就是Rot(k,θ)当kx=1，ky=0,kz=0的情况，将这些值代入式（1.32）得到10000cosθ-sinθ0Rot(x,θ)=0sinθcosθ0（1.33）0001这个结果与以前一样。 1.11等价旋转角与旋转轴（Equivalentangleandaxisofrotation）任给一个旋转变换，从（1.32）方程得到一个轴，绕这个轴旋转的等价旋转角可由如下方法得到。已知一个旋转变换Rnxoxax0nyoyay0R=nzozaz0（1.34）0001令R和式（1.32）的Rot(k,θ)相等，并将对角线各项相加得到nx+oy+az+1=k2xVersθ+cosθ+k2yVersθ+cosθ+k2zVersθ+cosθ+1（1.35）nx+oy+az=(k2x+k2y+k2z)Versθ+3cosθ=1+2cosθ（1.36）由此可得到旋转角的余弦是cosθ=1/2（nx+oy+az―1）（1.37）对非对角线项相减，我们得到oz―ay=2kxsinθ（1.38）ax―nz=2kysinθ（1.39）ny―ox=2kzsinθ（1.40）把式（1.38）到式（1.40）两边平方并相加有（oz―ay）2+（ax―nz）2+（ny―ox）2=4sin2θ（1.41） 我们得到了sinθ的表达式sinθ=±1/2√（oz―ay）2+（ax―nz）2+（ny―ox）2（1.42）规定这个旋转是绕k正方向旋转，当0≤θ≤180°时，在上式中取十号是合理的。这个旋转角θ被唯一定义为tanθ=√（oz―ay）2+（ax―nz）2+（ny―ox）2/（nx+oy+az―1）（1.43）k的各分量为kx=（oz―ay）/2sinθ（1.44）ky=（ax―nz）/2sinθ（1.45）kz=（ny―ox）/2sinθ（1.46）注意：当旋转角θ较小或接近180°时，上述三个式子的分子和分母都很小，所计算的k值是不精确的。为此可继续根据式（1.32）和式（1.33）对应元素以及它们的代数和相等的关系来求出k的各个分量。 1.12扩展与缩小（Stretchingandscaling）一个变换Ta0000b00T=00c0（1.47）0001将沿着x轴以a因子，沿着y轴以b因子，沿着z轴c因子均匀扩展着各种物体。假定在一个物体上任意一个点xi+yj+zk，它的变换是axa000xby0b00ycz=00c0z（1.48）100011这个正好表示出所说的扩展。这样，一个正方体可以由这个变换变成长方体。变换ss0000s00s=00s0（1.49）0001将以s为比例因子来扩展或缩小任一物体。 1.13透视变换（Perspectivetransformation）假设由一个简单透镜把一个物体形成的像如图1.17所示。透镜的轴沿着y的方向，焦距为f，物体上的一个点x,y,z成象为x/,y/,z/。y/表示象距，它随着物距y而变化。如果在通过y/而垂直于y的平面（照相机的底片）上画出各个点，那么就形成了一个透视像。射线穿过透镜中心不偏转，则z/y=z//y/（1.50）x/y=x//y/（1.51）根据平行透镜的轴的射线通过焦点，我们可以写出z/f=z//(y/+f)（1.52）x/f=x//(y/+f)（1.53）x/y/和z/是负数，而f是正数。用式（1.50）和式（1.52）消去y/，得z/f=z/(z/y/z+f)（1.54）zyx0(x’,y’,z’)(x,y,z)••f•图1.17透视变换 求出x/=x(1―y/f)（1.55）y/=y(1―y/f)（1.56）z/=z(1―y/f)（1.57）齐次变换p能导出同样结果，变换p是10000100p=0010（1.58）0-1/f01任何一点xi+yj+zk变换为x1000xy0100yz=0010z（1.59）1―y/f0-1/f011用比例因子1―y/f除得到的象点x/,y/,z/有[x/(1―y/f)]i+[y/(1―y/f)]j+[z/(1―y/f)]k（1.60）这个结果与前面利用透视原理的结果完全相同。在p变换的第二列最底一元素为―1/f，则导出一个沿着y轴的一透视变换。如果―1/f是第三列最底一项，那就是沿z轴的透视变换。 1.14变换方程（Transformequations）研究一下图1.18描述的一个物体与机械手情况，机械手用变换Z相对于基坐标系被定位。机械手的端点用变换ZT6来描述，而末端执行器用变换T6E来描述。物体用变换B相对于基坐标系被定位。最后，机械手末端抓手用变换BG相对于物体被定位。末端抓手位置的描述有两种方式，一种是相对于物体的描述，一种是相对于机械手的描述。由于两种方式描述的是同一个点，我们可以把这个描述等同起来，得到ZZT6T6E=BBG（1.61）这个方程可以用有向变换图来表示（见图1.19）。图的每一段弧表示一个变换。从它的定义的坐标系向外指向。用Z-1左乘和用E-1右乘方程（1.61），得到T6=Z-1BGE-1（1.62）0EGBZT6zyx图1.18一个物体与机械手•图1.19有向变换图GBET6Z••0 从有向变换图上我们可以直接得到上述结果，从T6弧线的尾部开始，沿着图形顺时针依次列出各个变换，直到T6弧的箭头为止。在逆变换时，我们从T6弧的箭头开始，按逆时针方向依次列出各个变换，直到T6弧的起始点为止，则可得到T6的逆T6-1=EG-1B-1Z（1.63）对上式求逆得到与式（1.62）完全相同的结果。作为进一步的例子，假设一个物体B的位置不知道，但机械手移动，使得末端抓手正好定位在物体上面。然后用G-1右乘式（1.61）求出B。或者在有向变换图中从B的尾部沿着逆时针方向到达弧B的箭头，直接得到同样结果。B=ZT6EG-1（1.64）同样，我们可以用有向变换图求出变换的连接组。例如ZT6=BGE-1（1.65）用有向变换图简化了变换方程的求解，可以直接写出变换结果。为了避免画圆，我们用图1.20所示的形式表示这个变换图，其中虚线表示那两个节点是被连在一起的，中间各垂线段表示相对坐标系。BGET6Z图1.20有向变换图的另一种形式 1.15小结（Summary）齐次变换可以用来描述空间坐标系的位置与方向。如果坐标系被固定在物体或机械手连杆上，那么该物体或机械手的位置与方向同样很容易被描述。物体A相对于物体B的齐次变换可以求其逆，来获得物体B相对于物体A的描述。变换可以表示为旋转变换和/或平移变换的乘积。如果变换是从左到右，那么旋转和/或平移是相对于当前的坐标系。如果变换是从右到左，那么旋转和/或平移是相对于参考坐标系进行。齐次变换用正交分量来描述坐标系，即用角度的正弦和余弦。这种描述可与旋转联系起来。在一般性旋转的情况下，旋转是绕任意向量旋转θ角。'