最新同济六版高等数学第三章第一节课件PPT课件 26页

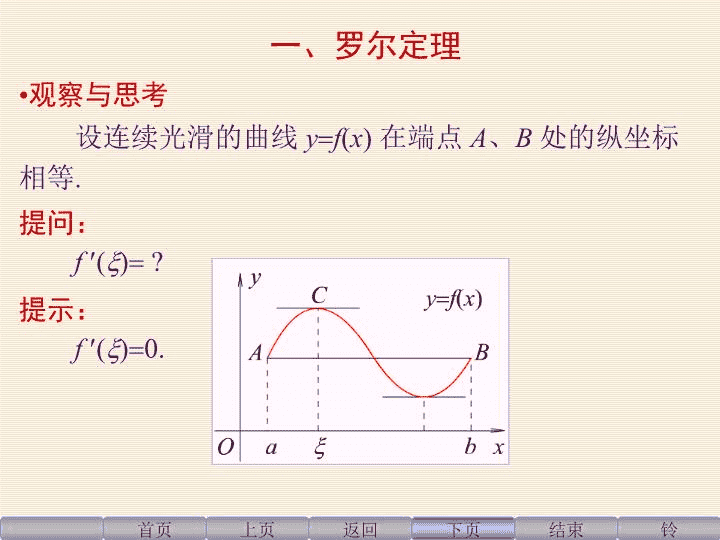
'同济六版高等数学第三章第一节课件 一、罗尔定理二、拉格朗日中值定理三、柯西中值定理§3.1中值定理上页下页铃结束返回首页 二、拉格朗日中值定理观察与思考设连续光滑的曲线y=f(x)在端点A、B处的纵坐标不相等提问：直线AB的斜率k=?f(x)?提示：下页直线AB的斜率 如果函数f(x)在闭区间[ab]上连续在开区间(ab)内可导那么在(ab)内至少有一点x使得f(b)f(a)f(x)(ba)拉格朗日中值定理下页直线AB的斜率 则函数j(x)在区间[ab]上满足罗尔定理的条件于是至少存在一点x(ab)使j(x)0即简要证明由此得f(b)f(a)f(x)(ba)下页如果函数f(x)在闭区间[ab]上连续在开区间(ab)内可导那么在(ab)内至少有一点x使得f(b)f(a)f(x)(ba)拉格朗日中值定理0 f(b)f(a)f(x)(ba)f(xDx)f(x)f(xqDx)Dx(0>> 证明设f(x)ln(1x)显然f(x)在区间[0x]上满足拉格朗日中值定理的条件根据定理就有f(x)f(0)f(x)(x0)0