最新多媒体教学课件ppt课件PPT课件 24页

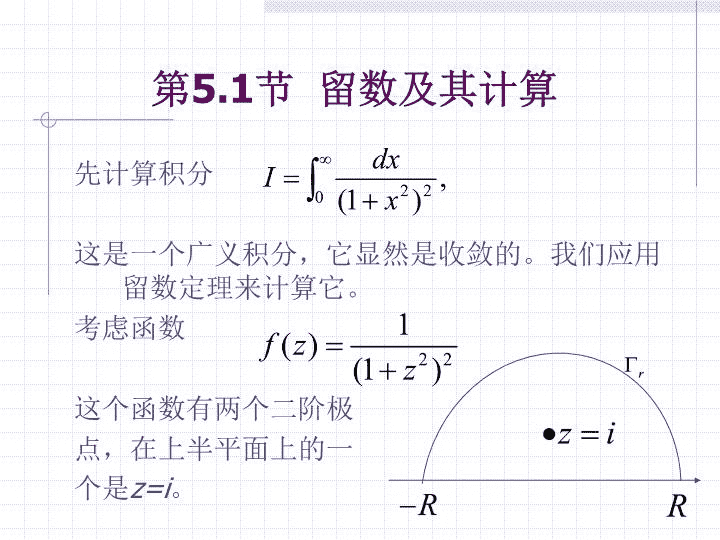
'多媒体教学课件ppt课件 第五章留数理论第5.1节留数及其计算第5.2节留数定理及其推广第5.3节应用于积分计算第5.4节辐角原理和儒歇定理 注解注解2、即f(z)在孤立奇点z0的留数等于其洛朗级数展式中的系数。注解3、如果z0是f(z)的可去奇点，那么 留数的求法方法一：前述方法二：设z0为f的一阶极点，则方法三：其中P(z)及Q(z)在解析，且 留数的求法方法四：。设z0是f(z)的一个m阶极点(m>1)。则在z0附近有其中，在z0解析，且，则因此 2.在无穷远点的留数设函数f(z)在圆环域R<|z|<内解析,C为圆环域内绕原点的任何一条简单闭曲线,则积分的值与C无关,称其为f(z)在点的留数,记作f(z)在圆环域R<|z|<内解析：理解为圆环域内绕的任何一条简单闭曲线。 这就是说,f(z)在点的留数等于它在点的去心邻域R<|z|<+内洛朗展开式中z-1的系数变号. 第5.2节留数定理及其推广定理5.1（留数定理）设D是由复合闭路所围的有界多连通域。设f(z)在D内除去有孤立奇点外解析，并且连续到C，则：这里沿C的积分按关于区域D的正向取的。 留数定理的基本思想 留数定理的证明：证明：以D内每一个孤立奇点zk为心，作圆Ck，使以它为边界的闭圆盘上每一点都在D内，并且使任意两个这样的闭圆盘彼此无公共点。从D中除去以这些Ck为边界的闭圆盘的一个区域G，其边界是C以及Ck，在G及其边界所组成的闭区域上，f(z)解析。因此根据柯西定理， 这里沿C的积分按关于区域D的正向取的，沿Ck的积分按反时针方向取的。根据留数的定义，得定理的结论成立。留数定理的证明：注解1、留数定理在两个从定义上看，完全不同，也不相干的概念之间架起一个桥梁，是非常重要的。注解2、具体计算一定要注意前面的系数 定理5.2如果f(z)在扩充复平面内只有有限个孤立奇点,那末f(z)在所有各奇点(包括点)的留数总和必等于零.证：除点外,设f(z)的有限个奇点为zk(k=1,2,...,n).且C为一条绕原点的并将zk(k=1,2,...,n)包含在它内部的正向简单闭曲线,则根据留数定理与在无穷远点的留数定义,有注：定理5.2给出了扩充复平面内只有有限个孤立奇点时的关系，是一个方程，说明此类问题实际计算时可以转化求解； 所以方法五成立. 例5.9发现在|z|<4有五个孤立起点，故可以将问题转化为求无穷远点的留数 2.推广的留数定理若孤立起点在边界上时，可以将留数定理进行推广：设D是由复合闭路所围成的有界多连通域，，f(z)在D内解析，在连续，在有关于D的阶极点（），则其中，L取关于D的正向，是处关于域D的张角 2.推广的留数定理定理5.3(路见可定理）设D是由复合闭路所围成的有界多连通域，，设函数f(z)在内解析,在连续，f(z)在分别有关于D的阶极点j=1,2…,N)，则其中为处关于D的张度，L取关于D的正向，积分在每个处在高阶奇异积分（重极点时）或柯西主值（单极点时）意义下理解。 结束语谢谢大家聆听！！！24'