最新大学物理下册干涉习题课件PPT课件 18页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。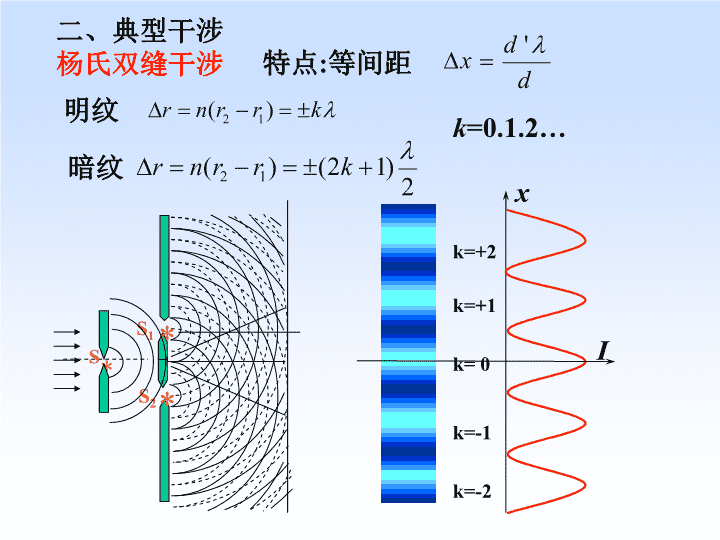　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅大学物理下册干涉习题课件 杨氏双缝干涉特点:等间距二、典型干涉明纹暗纹k=0.1.2…*SS2**S1k=+1k=-2k=+2k=0k=-1Ix 例7：在迈克尔逊干涉仪的一条光路中，插入一块折射率为n，厚度为d的透明薄片。插入这块薄片使这条光路的光程改变了2(n-1)d例8：若在迈克尔逊干涉仪的可动反射镜M移动0.620mm的过程中，观察到干涉条纹移动了2300条，则所用光波的波长为Å 例9.如图，S1、S2是两个相干光源，它们到P点的距离分别为r1和r2．路径S1P垂直穿过一块厚度为t1，折射率为n1的介质板，路径S2P垂直穿过厚度为t2，折射率为n2的另一介质板，其余部分可看作真空，这两条路径的光程差等于A.B.C.D.答：B 例10双缝干涉实验装置如图所示，双缝与屏之间的距离D＝120cm，两缝之间的距离d＝0.50mm，用波长l＝500nm(1nm=10-9m)的单色光垂直照射双缝．(1)求原点O(零级明条纹所在处)上方的第五级明条纹的坐标x．(2)如果用厚度l＝1.0×10-2mm，折射率n＝1.58的透明薄膜复盖在图中的S1缝后面，求上述第五级明条纹的坐标x． =19.9mm解：(1)∵dx/D≈kλx≈Dkl/d=(1200×5×500×10-6/0.50)mm=6.0mm(2)考虑零级明条纹，零级明纹上移零级上方的第五级明条纹坐标 如图半导体测硅片表面氧化膜，腐蚀成劈尖形，用钠光＝5893Å照射，在氧化膜表面恰好看到五个明纹。求（1）最大膜厚dmax；（2）若d=0.6m，用绿光＝550nm，可见几条亮纹？解（1）无半波损失氧化膜硅k=0,1,2,...因为可见5条明纹，所以k＝4（2）所以k=3，可见四条亮条纹 在双缝干涉实验中，屏幕E上的P点处是明条纹．若将缝S2盖住，并在S1S2连线的垂直平分面处放一高折射率介质反射面M，如图所示，则此时(A)P点处仍为明条纹．(B)P点处为暗条纹．(C)不能确定P点处是明条纹还是暗条纹．(D)无干涉条纹．答：B 例:在双缝干涉实验中，若单色光源S到两缝S1、S2距离相等，则观察屏上中央明条纹位于图中O处．现将光源S向下移动到示意图中的S位置，则(A)中央明条纹也向下移动，且条纹间距不变．(B)中央明条纹向上移动，且条纹间距不变．(C)中央明条纹向下移动，且条纹间距增大．(D)中央明条纹向上移动，且条纹间距增大．答:B 例:在双缝干涉实验中，波长l＝550nm的单色平行光垂直入射到缝间距a＝2×10-4m的双缝上，屏到双缝的距离D＝2m．求：(1)中央明纹两侧的两条第10级明纹中心的间距；(2)用一厚度为d＝6.6×10-5m、折射率为n＝1.58的玻璃片覆盖一缝后，零级明纹将移到原来的第几级明纹处？(1nm=10-9m)解：(1)Dx＝20Dl/a＝0.11m(2)覆盖云玻璃后，零级明纹应满足(n－1)d＋r1＝r2设不盖玻璃片时，此点为第k级明纹，则应有r2－r1＝kl所以(n－1)d=klk＝(n－1)d/l＝6.96≈7零级明纹移到原第7级明纹处 例:在图示的双缝干涉实验中，若用薄玻璃片(折射率n1＝1.4)覆盖缝S1，用同样厚度的玻璃片(但折射率n2＝1.7)覆盖缝S2，将使原来未放玻璃时屏上的中央明条纹处O变为第五级明纹．设单色光波长l＝480nm(1nm=109m)，求玻璃片的厚度d(可认为光线垂直穿过玻璃片)．解：原来，覆盖玻璃后∴(n2－n1)d＝5l=8.0×10-6m 结束语谢谢大家聆听！！！18'