西北工业大学矩阵论课件PPT第五章例题特征值的估计与表示 27页

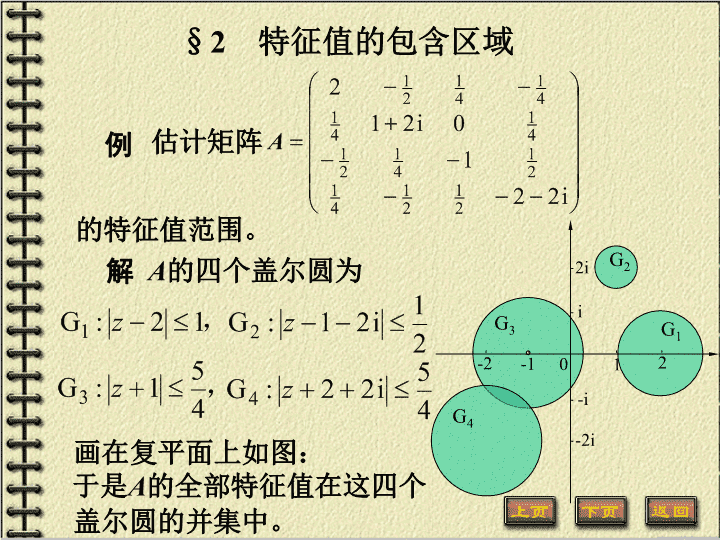
'例解所以又因为所以估计矩阵的特征值上界。因为0.50第五章特征值的估计与表示§1特征值的界的估计 实际计算可求得A的特征值为估计的效果较好。由于A是实矩阵，所以即A的特征值在虚轴上区间之内。 G3G1例解A的四个盖尔圆为画在复平面上如图：于是A的全部特征值在这四个估计矩阵的特征值范围。012-1-2i2i-i-2iG2G4盖尔圆的并集中。§2特征值的包含区域 例满足应用Gerschgorin定理证明A的特征值的实部小于零。证从而由知A的第i个盖尔圆在左半平面，故A的特征值的实部小于零。设矩阵因为 例解A的四个盖尔圆为估计矩阵的特征值范围。 G3G1012-1-2i2i-i-2iG2G4A的四个列盖尔圆为画在复平面上如图：可见A的四个特征值位于中，四个孤立圆盘且各圆盘中仅有A的一个特征值。 例分布范围，解A的三个盖尔圆为试估计矩阵的特征值并适当选择一组正数，使A的三个盖尔圆互不相交。作图:G3G2G100.51.0 G2取则B的三个盖尔圆为：G3G100.51.0综合考虑知，中各有A的一个特征值。在 G2G3G1例解A的三个盖尔圆为：取则试分离矩阵的特征值。039i作图： 中各有A的一个特征值。综合考虑知，在G1，B的三个盖尔圆为：G2G3G1039i作图： G1G4G2例的特征值(要求画图表示)，A的四个盖尔圆为应用盖尔定理隔离并利用实矩阵特征值解的性质改进所得结果。作图：0310-2G3 取则B的四个盖尔圆为作图：G1G4G20310-2G3 故在中各有A的一个特征值。于是在区间中各有A的一个特征值。 G2G1G3例并在复平面上画图。A的三个盖尔圆为：试分离矩阵的特征值，解作图：应取但G1与G2靠太近，无法分。01020 G1例并在复平面上画图。试分离矩阵的特征值，解AT的三个盖尔圆为：作图：G2G301020 取则B的三个盖尔圆为：作图：G1G2G301020它们已分离，中各有A的一个特征值。故在 例解A的三个盖尔圆为隔离矩阵的特征值(要求画图表示)。作图：01020 取令则B的三个盖尔圆为作图：01020在中各有A的一个特征值。 G1G2G3例的特征值A的三个盖尔圆为：试估计矩阵分布区域。解作图：0123 而A的三个Ostrowski圆为（取G1G2作图：0123O3G3O1O2 G1G2例的特征值分布区域。A的两个盖尔圆为：试估计矩阵解00.51.0作图：A的一个Cassini卵形为： 令则由得Cassini卵形线其中心在左端点右端点最高点最低点可见结果较为精确，的标准方程不过Cassini卵形线比较难画。作图：G1G200.51.0 例的奇异值为又设则分析设的特征值为故§3实对称矩阵特征值的表示 例其中求解广义特征值问题解§4广义特征值问题 广义特征值为求解得对应的广义特征向量为求解得对应的广义特征全部广义特征向量为全部广义特征向量为向量为 例求B-正交矩阵Q使得解广义特征值为对应的广义特征向量分别为已知实对称矩阵A和正定矩阵B分别为为对角矩阵。先求解广义特征值问题 故B-正交矩阵使得（它们已是B-正交的）按B-单位化得'