数学人教版八年级上册线段的垂直平分线.1.2线段垂直平分线的性质课件PPT.ppt 31页

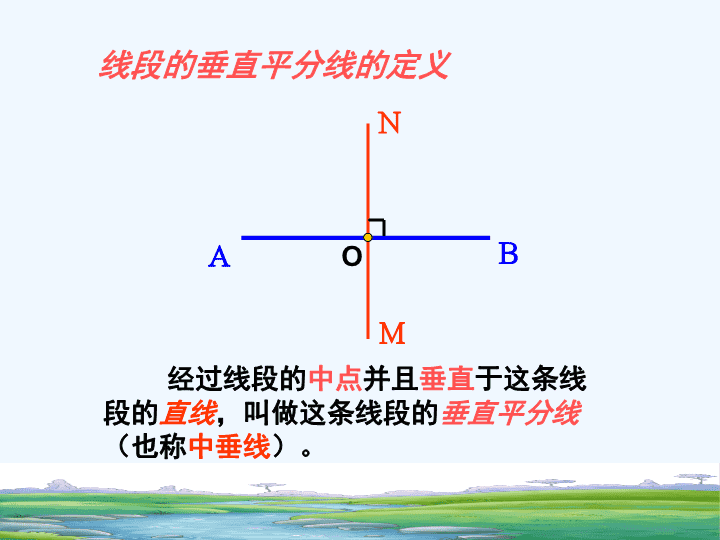
'线段的垂直平分线 比较归纳：轴对称图形两个图形成轴对称区别＿个图形＿个图形联系１．沿一条直线折叠,直线两旁的部分能够＿＿＿＿．２．都有＿＿＿＿．３．如果把一个轴对称图形沿对称轴分成两个图形，那么这两个图形关于这条直线＿＿＿；如果把两个成轴对称的图形看成一个图形，那么这个图形就是＿＿＿＿．一两互相重合对称轴对称轴对称图形 经过线段的中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线（也称中垂线）。线段的垂直平分线的定义ＡＢＮＭO 1、如果两个图形关于某条直线对称，那么对称轴是任何一对应点连线段的垂直平分线2、轴对称图形的对称轴，是任何一对应点所连线段的垂直平分线l垂直平分l垂直平分l垂直平分图形轴对称的性质 线段AB的中垂线MN，垂足为C；在MN上任取一点P，连结PA、PB；量一量：PA、PB的长，你能发现什么？PMNCPA=PBP1A=P1B……由此你能得到什么规律？命题：线段垂直平分线上的点和这条线段两个端点的距离相等。画一画AB●P1 命题：线段垂直平分线上的点和这条线段两个端点的距离相等。已知：如图，直线MN⊥AB,垂足为C,且AC=CB.点P在MN上.求证：PA=PB证明：∵MN⊥AB∴∠PCA=∠PCB在ΔPAC和ΔPBC中，AC=BC∠PCA=∠PCBPC=PC∴ΔPAC≌ΔPBC∴PA=PB证一证ABPMNC 性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等。ABPMNCPA=PB点P在线段AB的垂直平分线上性质定理有何作用？可证明线段相等定理应用格式：∵AC=BC,MN⊥AB,P是MN上任意一点∴PA=PB(线段垂直平分线性质)线段垂直平分线性质 ABPCPA=PB点P在线段AB的垂直平分线上（利用全等,仿照性质定理自己证明）反过来，如果PA=PB，那么点P是否在线段AB的垂直平分线上?换一换判定定理：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。判定定理有何作用？用途：判定一条直线是线段的中垂线 判定定理：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上判定ABPC性质题设和结论正好相反，是互逆关系线段垂直平分线性质 用一根木棒和一根弹性均匀的橡皮筋，做一个简易的“弓”，“箭”通过木棒中央的孔射出去，怎样才能保持射出去的方向与木棒垂直呢？只要AC=BC就可以了ABC为什么？ （1）线段AB的垂直平分线上的所有点都满足“与点A、B的距离相等”这一条件吗？线段的垂直平分线可以看作是和线段两个端点距离相等的所有的点的集合想一想（2）满足“与A、B的距离相等”的所有点都在线段AB的垂直平分线上吗？ 1、如图直线MN垂直平分线段AB，则AE=AF判断题课堂练习ABMEFN 2、如图线段MN被直线AB垂直平分，则ME=NE√课堂练习判断题ABMNE 3、如图PA=PB，则直线MN是线段AB的垂直平分线。课堂练习ABMNP 二、逆定理：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。线段的垂直平分线一、性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上线段垂直平分线判定线段垂直平分线性质三、线段的垂直平分线的集合定义：线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合小结 13.3角的平分线ODEABPC定理1在角的平分线上的点到这个角的两边的距离相等。定理2到一个角的两边的距离相等的点，在这个角的平分线上。角的平分线是到角的两边距离相等的所有点的集合14.1线段的垂直平分线定理线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线 理解了吗？1、∵，∴AB＝AC。理由：2、∵，∴A在线段BC的中垂线上理由：AD是BC的中垂线AB＝AC线段垂直平分线上的点与这条线段两个端点的距离相等．与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。BCAD3、如图，NM是线段AB的中垂线,下列说法正确的有：。①AB⊥MN,②AD=DB，③MN⊥AB，④MD=DN，⑤AB是MN的垂直平分线ABMND①②③ 3、下列说法：①若直线PE是线段AB的垂直平分线，则EA=EB，PA=PB；②若PA=PB，EA=EB，则直线PE垂直平分线段AB；③若PA=PB，则点P必是线段AB的垂直平分线上的点；④若EA=EB，则过点E的直线垂直平分线段AB．其中正确的个数有（　　）A．1个B．2个C．3个D．4个C 会用吗？4如图，若AC=12，BC=7，AB的垂直平分线交AB于E，交AC于D，求△BCD的周长。DCBEA解：∵ED是线段AB的垂直平分线∴∵C△BCD=BD+DC+BC∴C△BCD===BD=ADAD+DC+BCAC+BC12+7=19 1.垂直平分线的定义：∵MN是AB的垂直平分线∴，；2.垂直平分线的性质：∵MN是AB的垂直平分线∴（）3.垂直平分线的判定：∵PA＝PB∴（）小结MN⊥ABPABMNDAD＝BDPA＝PB线段垂直平分线上点与这条线段两个端点的距离相等P在AB的垂直平分线上与一条线段两个端点距离相等的点，在这条线段的垂直平分线上 1、如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上，AB、AC、CE的长度有什么关系？AB+BD与DE有什么关系？AC=CEAB+BD=DEECDBA课堂练习 2、如图，AB=AC，MB=MC，直线AM是线段BC的垂直平分线吗？ABCM课堂练习 3、如图，△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，求△ABC的周长？ECDBA课堂练习 4、如图，△ABC中，BC的垂直平分线分别交AC、BC于点E、D，△ABE的周长为15，BD=5，求△ABC的周长？ECDBA课堂练习 5、如图△ABC中，AC＝20cm，DE垂直平分AB，若BC=12cm，求△BCD的周长。DCEBA课堂练习 6、如图△ABC中，AB=AC＝32，DE是AB的垂直平分线，且有BC=21，求△BCD的周长。DCEBA课堂练习 例1：如图，点A与点B关于某条直线成轴对称，你能作出这条直线吗？例题精讲AB分析：我们只要连接点A和点B，画出线段AB的垂直平分线，就可以得到点A和点B的对称轴.而由两点确定一条直线和线段垂直平分线的性质，只要作出到点A、B距离相等的两点即可.作法：1.分别以点A、B为圆心，以大于1/2AB的长为半径作弧，两弧交于C、D两点；2.作直线CD.CD∴直线CD即为所求 例2：如图是一颗五角星，你能作出它的所有对称轴吗？例题精讲作法：1.找出它的一对对称点（例如A和A’）；2.作线段AA’的垂直平分线l.AA’l用类似的的方法，就可以作出其他四条对称轴.你也试一试！ 已知：△ABC中，边AB、BC的垂直平分线交于点P。求证：PA=PB=PC.PABC结论：三角形三边的垂直平分线交于一点，并且这点到三个顶点的距离相等。证明：∵MN⊥AB，P在MN上∴PA=PB（线段垂直平分线上的点与线段两个端点的距离相等）同理：PB=PC∴PA=PB=PCMFEN 如图，八（5）班与八（6）班两个班的学生分别在M、N两处参加植树劳动，现要在道路AO、BO的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且PM=PN，请你找出P点。MNABO做一做 如图,已知:AOB,点M、N.求作:一点P,使点P到AOB两边的距离相等,并且满足PM=PN...MNAOB.P点P为所求作的茶水供应点P'