自动控制理论课件PPT2(哈工大).ppt 84页

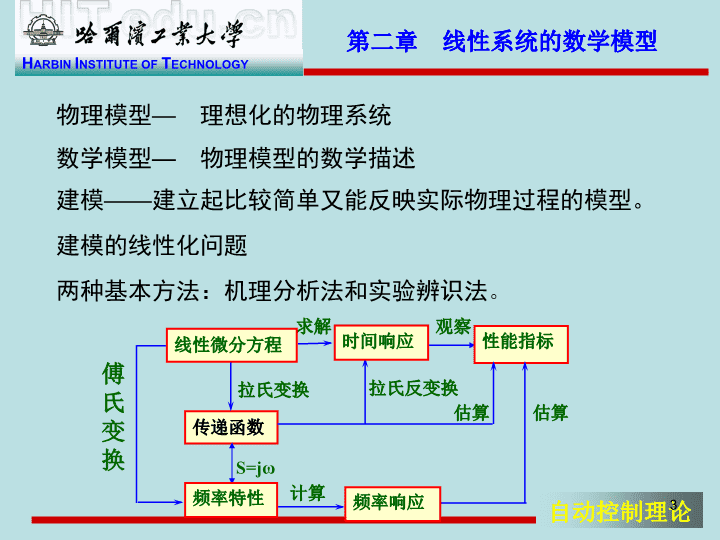
'本章重点线性系统微分方程的建立；运用拉氏变换法求解线性微分方程；传递函数的概念和性质；传递函数和微分方程之间的关系；结构图的绘制及其等效变换；结构图和信号流图的关系；梅逊公式。1 本章难点运用综合的基础知识(如电子、机械、物理等知识)建立正确的微分方程；(2)建立系统的结构图或信号流图；(3)结构图和信号流图等效变换的灵活运用；(4)建立系统的动态方程。2 第二章　线性系统的数学模型物理模型—　理想化的物理系统数学模型—　物理模型的数学描述建模——建立起比较简单又能反映实际物理过程的模型。建模的线性化问题两种基本方法：机理分析法和实验辨识法。求解观察线性微分方程性能指标传递函数时间响应频率响应拉氏变换拉氏反变换估算估算计算傅氏变换S=jω频率特性3 §2.1线性系统的输入—输出时间函数描述§2.2线性系统的输入—输出传递函数描述§2.3典型环节的数学模型§2.4控制系统的结构图及其等效变换§2.5自动控制系统的传递函数第二章　线性系统的数学模型4 第二章　线性系统的数学模型§2.1线性系统的输入—输出时间函数描述系统的输入—输出描述：是一种外部描述，目的在于通过该数学模型确定被控制量与给定量或扰动量之间的关系。一、列写微分方程法（机理分析法）1.　线性元件的微分方程(1)确定输入量、输出量和扰动量，并根据需要引进一些中间变量。(2)根据物理或化学定律，列出微分方程。(3)消去中间变量后得到描述输出量与输入量(包括扰动量)关系的微分方程（标准形式）。5 第二章　线性系统的数学模型例2.1　弹簧阻尼系统f—粘滞摩擦系数k—弹簧系数v—物体相对的移动速度6 例2.1　机械传递系统xa和xb作为网络的结点。在每一个节点上，力的和等于零。综合两个方程可以得到：“D”表示微分算子第二章　线性系统的数学模型7 第二章　线性系统的数学模型G＝G1G28 第二章　线性系统的数学模型例2-2　　机械旋转系统f—粘滞摩擦系数k—弹性扭转变形系数9 第二章　线性系统的数学模型例2-3电阻、电感、电容串联网络机械传递系统电气网络fvMKBx力速度质量弹性系数阻尼系数线位移uiL1/CRq电压电流电感电容倒数电阻电荷10 第二章　线性系统的数学模型例2-4　直流他激电动机带动负载设激磁电流恒定并忽略电枢反应。ω为转速，Ua为电枢电压，Mc为负载1)电枢回路的电势平衡方程为：2)电动机的反电势方程为Ce为电动机的电势常数，单位为v·s／rad。3)电动机的电磁转矩方程为Cm为电动机的转矩常数，单位为Nm／A。11 第二章　线性系统的数学模型4)电动机轴上的动力学方程为J为转动部分折算到电动机轴上的总转动惯量，其单位为N·m·s2。消去ea、ia、M三个中间变量，可以得到描述输出量ω，输入量ua及扰动量M之间的关系的微分方程为：电机的电磁时间常数电机的机械时间常数电压传递系数转矩传递系数12 第二章　线性系统的数学模型通常电枢的电感La很小，所以电磁时间常数可以忽略不计，于是电动机的微分方程可以简化为：如果取电动机的转角作为输出，则上式可改写为2　微分方程的增量化表示若电动机处于平衡状态，各阶导数均等于零，微分方程可以变为下面的代数方程：表示平衡状态下的输入量和输出量的关系，称为静态方程，表示了电机的控制特性和机械特性。13 第二章　线性系统的数学模型电动机在平衡状态附近运行的变量可以表示为：将上面变量代回到简化的微分方程中，并考虑平衡状态的变量关系可以得到这是电动机的微分方程在平衡状态附近的增量化表示式。14 第二章　线性系统的数学模型3　非线性方程的线性化非线性方程难于求解，用线性数学模型近似表示非线性数学模型。在一定工作范围内进行线性化处理。将非线性函数在平衡点附近展成泰勒级数，并忽略高次项。例：直流发电机X轴表示励磁电流Y轴表示输出电势由于存在磁路饱和，y和x呈非线性关系y=f(x)可以在(x0,y0)附近泰勒级数15 第二章　线性系统的数学模型忽略高次项，然后用增量表示是比例常数。经上述处理后，就变成了线性方程。16 第二章　线性系统的数学模型对于具有两个自变量的非线性函数在静态工作点y0=(x10,x20)附近展成泰勒级数。用增量表示及是比例常数。17 第二章　线性系统的数学模型上述方法称为小偏差线性化方法。它是基于这样一种假设：输入量和输出量只是在静态工作点附近作微小变化。几点注意：(1)只适用于不太严重的非线性系统，其非线性函数是可以利用泰勒级数展开的（非本质非线性）。(2)实际运行情况是在某个平衡点(即静态工作点)附近，且变量只能在小范围内变化。(3)不同静态工作点得到的方程是不同的。(4)对于严重的非线性，例如继电特性，因为处处不满足泰勒级数展开的条件，故不能做线性化处理。(5)线性化后得到的是增量微分方程。18 第二章　线性系统的数学模型二、脉冲响应法（实验辩识法）描述线性定常系统的微分方程为：实验辨识方法的理论依据：C(t)=H(t)r(t)假设线性系统是定常的，初始条件为零或初始状态为零，其响应和输入之间满足齐次和线性关系，即：19 第二章　线性系统的数学模型给定输入是单位脉冲函数时实验辨识基本原理脉冲函数的表达式为：A为脉冲面积或脉冲强度。脉冲强度A=1时的脉冲函数记为，令并求取极限，则称为单位脉冲函数。，令20 第二章　线性系统的数学模型零初始条件的线性定常系统的输入δ(t)，得到的输出称为系统的单位脉冲响应，也称为权函数，记作g(t)。21 第二章　线性系统的数学模型§2.2线性系统的输入—输出传递函数描述为什么采用传递函数来描述？微分方程描述不直观、求解困难。线性常微分方程经过拉氏变换，即可得到系统在复数域中的数学模型，称之为传递函数。将单位脉冲响应g(t)的曲线转换成相应的传递函数。表示其输入输出关系。22 第二章　线性系统的数学模型R(s)输入r(t)的像函数，即输入函数的拉氏变换；C(s)输出c(t)的像函数，即输出函数的拉氏变换。传递函数——初始条件为零的线性定常系统输出的拉氏变换与输入的拉氏变换之比。也称为频（率）域描述。几点说明：只适用于线性定常系统。是系统的动态数学模型。分母的阶数一定高于分子的阶数。(为什么？）有惯性元件和受到功率的限制23 第二章　线性系统的数学模型客观物理世界的基本属性，它反映了一个基本事实：一个物理系统的输出不能完全复现输入信号，只有经过一定的时间过程后，输出量才能达到输入量所要求的数值。一个传递函数只能表示一个输入量对一个输出量的关系。单输入-单输出系统，若多输入多输出要采用传递函数矩阵。传递函数可以表示成有理分式，也可以表示成零极点表示的形式。也可以表示成时间常数的形式K值具有量纲也称为传递系数24 第二章　线性系统的数学模型7.分子分母的系数都是实数，所以如果有复数零极点则必为共轭复数。式中，25 第二章　线性系统的数学模型复习－拉氏变换（Laplacetransform）拉氏变换的定义t<0时f(t)=02.几个简单的函数的拉氏变换单位阶跃指数函数26 第二章　线性系统的数学模型余弦函数27 第二章　线性系统的数学模型单位斜坡函数3.拉氏变换的一些性质线性性质叠加性质28 第二章　线性系统的数学模型延迟性质像函数（复域）的微分相似定理本函数（时域）的微分29 第二章　线性系统的数学模型例：复域延迟性质例：已知30 第二章　线性系统的数学模型终值定理：有存在的条件f(t)及其导数是可拉氏变换的，且要sF(s)在虚轴（除原点）和右半平面上没有极点。初值定理：卷积定理：已知函数f(t)和g(t)，其卷积定义为31 第二章　线性系统的数学模型3.拉氏反变换求本函数（1）部分分式分解法极点的几种情形：都是一阶实极点。32 第二章　线性系统的数学模型例：已知：计算f(t)重的一阶实极点33 第二章　线性系统的数学模型含有共轭极点。2.留数方法（略）34 第二章　线性系统的数学模型例：直流电动机传递函数电枢电势平衡方程：反电势方程：电磁转矩方程电机轴上转矩平衡方程当Mc(s)=0时－机电时间常数－电磁时间常数忽略Ta35 第二章　线性系统的数学模型直流电动机动态方框图当Mc(s)=0时36 例：直流电动机转速闭环控制系统第二章　线性系统的数学模型37 第二章　线性系统的数学模型直流电机传函对放大器对测速机闭环系统的传递函数38 第二章　线性系统的数学模型用复数阻抗法求电网络的传递函数时域方程拉氏变换传递函数复数阻抗电容电感电阻39 第二章　线性系统的数学模型B点为虚地例：比例积分控制器40 第二章　线性系统的数学模型例：比例微分控制器静态放大系数41 第二章　线性系统的数学模型§2.3典型环节的数学模型典型环节：运动规律相同，具有相同的数学模型。一、比例环节K称为比例系数或放大系数，有时也称为环节的增益。二、惯性环节τ－时间常数，K－比例系数输出量不能立即跟随输入量变化。存在时间上的延迟。可以用τ来量度。42 第二章　线性系统的数学模型对惯性环节输入单位阶跃信号并且具有零初始条件时，其输出量y(t)为：43 第二章　线性系统的数学模型三、积分环节积分环节的动态方程为积分环节在单位阶跃输入下的响应K－比例系数，T－积分时间常数。44 第二章　线性系统的数学模型四、微分环节，τ—时间常数。纯微分一阶微分二阶微分45 第二章　线性系统的数学模型输入是单位阶跃响应，即r(t)=1(t)，则输出的单位阶跃响应为：几个实际微分的例子RC串联电路τ＝RC　—时间常数46 第二章　线性系统的数学模型实际的比例微分电路47 第二章　线性系统的数学模型五　振荡环节弹簧阻尼系统的传递函数为：机械旋转系统的传递函数为：RLC电路的传递函数为：振荡环节的微分方程为传递函数为：48 第二章　线性系统的数学模型设0<ζ<1，K=1,输入信号r(t)=1(t)，R(s)=1/s，求阶跃响应。令无阻尼自然振荡频率阻尼自然振荡频率49 第二章　线性系统的数学模型如果令50 振荡环节的单位阶跃响应第二章　线性系统的数学模型51 第二章　线性系统的数学模型六、纯滞后环节输出信号比输入信号迟后一段时间。c(t)=r(t-τ)τ－滞后时间常数。得到传递函数52 §2-4控制系统的结构图及其等效变换第二章　线性系统的数学模型一、结构图的基本概念把方块图和传递函数结合起来。称为动态结构图。是描述系统各组成元件之间信号传递关系的一种数学图形。两种图形研究方法：方框图和信号流程图方法。结构图给出了信息传递的方向又给出了输入输出的定量关系。即C(s)=R(s)G(s)。53 第二章　线性系统的数学模型二、结构图的组成和建立由四种基本图形符号组成。（1）函数方块(2)信号线(3)分支点(引出点)（4)综合点(比较点或相加点)54 2．系统结构图的建立55 第二章　线性系统的数学模型三、结构图的等效变换常用的结构图变换方法有二：一是环节的合并，二是信号分支点或相加点的移动。原则是：变换前、后的数学关系(输入量、输出量）保持不变。1.环节的串联忽略负载效应56 例：左图并不是两个惯性环节串联其传递函数为如果忽略负载效应。57 2.环节的并联58 第二章　线性系统的数学模型3.反馈联接对于正反馈有当H(s)=1有59 第二章　线性系统的数学模型4.汇合点和分支点的移动和互换以及方框图的变换和简化将信号引出点和汇合点前后移动的规则：变换前和变换后前向通道中的传递函数的乘积保持不变；变换前和变换后回路中的传递函数的乘积保持不变。（1）信号相加点(综合点)的移动和互换相加点后移：60 第二章　线性系统的数学模型相加点前移：相加点互换：61 第二章　线性系统的数学模型（2）分支点的移动和互换分支点后移：分支点前移：62 第二章　线性系统的数学模型分支点互换（1）结构图简化的关键是解除环路与环路的交叉，使之分开或形成大环套小环的形式。（2）解除交叉连接的有效方法是移动相加点或分支点。一般，相邻的分支点和综合点可以彼此交换。（3）当分支点与综合点相邻时，它们的位置就不能作简单的交换。63 引出点移动G1G2G3G4H3H2H1abG1G2G3G4H3H2H1G4164 G2H1G1G3综合点移动G1G2G3H1错！G2无用功向同类移动G165 G1G4H3G2G3H1作用分解H1H3G1G4G2G3H3H166 归纳出以下几条简化结构图的规律(1)闭环系统传递函数Φ(s)是一个有理分式。(2)其分子等于前向通道中各串联环节的传递函数之积(3)分母为负反馈为“＋”；正反馈为“－”。67 §2-5自动控制系统的传递函数一、系统的开环传递函数前向通道传递函数和反馈通道传递函数的乘积。将反馈点上断开主反馈通道，反馈信号和偏差信号之比就是开环传递函数。二、闭环系统的传递函数68 给定输入作用下的闭环传递函数N(s)＝0时的系统结构图2．扰动输入作用下的闭环传递函数R(s)＝0时的系统结构图69 3．给定输入和扰动输入同时作用下系统的总输出三、闭环系统的偏差传递函数1.给定输入作用下的偏差传递函数。N(s)=0时E(s)和R(s)之比。N(s)=0时系统的等效图70 2．扰动输入作用下的偏差传递函数3．给定输入和扰动输入同时作用下的总偏差71 注：四个传函具有相同的分母。上式称为闭环系统的特征多项式。上式称为闭环系统的特征方程。特征方程的根称为闭环系统的根或闭环系统的极点。72 §2-6信号流程图一、基本概念是一种将线性代数方程用图形表示的方法。支路有三个特点：联接有因果关系的节点；有方向性；有加权性。73 二、一些术语和定义节点：表示变量或信号的点。支路：起源于一个节点，终止于另一个节点，这两个节点之间不包含或经过第三个节点。出支路：离开节点的支路。入支路：指向节点的支路。源(节)点：只有出支路的节点，对应于自变量或外部输入，如x0。汇节点：只有入支路的节点，对应于因变量，如x6。74 开通道：如果通道从某节点开始终止在另一节点上，而且通道中每个节点只经过一次，则该通道称为开通道。通道：又称路径，从一个节点出发，沿着支路的箭头方向相继经过多个节点的支路。混合节点：节点既连接入支路又连接出支路。闭通道：如果通道的终点就是通道的始点，并且通道中每个节点只经过一次，该通道称为闭通道或反馈环、回环、回路等。如果从一个节点开始，只经过一个支路又回到该节点的，称为自回环。75 前向通道：在开通道中，从源节点开始到汇节点终止，而且每个节点只通过一次的通道，称为前向通道。不接触回环：如果一些回环没有任何公共节点，就称它们为不接触回环。支路传输：两个节点之间的增益。通道传输或通道增益：沿通道各支路传输的乘积。回环传输或回环增益：闭通道中各支路传输的乘积。三、信号流图的简化76 混合节点的消除回路的消除自回路的消除串联支路的合并并联支路的合并77 四、梅逊(Mason)公式及其应用梅逊公式为：T—从源节点到任何节点的传输；Pk—第k条前向通道的传输；Δ—信号流图的特征式ΣL1—为所有不同回环的传输之和；ΣL2—为任何两个不互不接触的回环传输的乘积之和；ΣL3—为任何三个不互不接触的回环传输的乘积之和；ΣLm—为任何m个不互不接触的回环传输的乘积之和；Δk—为余子式，即从Δ中除去与第k条前向通道Pk相接触的回环的回路增益后余下的部的特征式。78 例1：系统只有一个回路增益为-G2G3H两条前向通道：其余子式其余子式79 三条前向通道：回路增益：L1=-G1G2G3G4H2L2=-G1G6H2L3=-G3H1L2和L3互不接触，所以特征式为：P1=G1G2G3G4，P2=G3G4G5P3=G1G680 R(s)C(s)L1=–G1H1L2=–G3H3L3=–G1G2G3H3H1L4=–G4G3L5=–G1G2G3L1L2=(–G1H1)(–G3H3)=G1G3H1H3L1L4=(–G1H1)(–G4G3)=G1G3G4H1G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H3(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G1(s)G2(s)G3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)G4(s)G3(s)梅逊公式例R-CH1(s)H3(s)G1(s)G2(s)G4(s)H1(s)H3(s)G1(s)G2(s)G3(s)P2=G4G3P1=G1G2G3△1=1△2=1+G1H1C(s)R(s)=?请你写出答案，行吗？81 四个单独回路，两个回路互不接触e1abcdfghC(s)R(s)C(s)R(s)=1––––++前向通路两条信号流图afbgchefhgahfced(1g)–bdabc82 G1(s)G3(s)H1(s)G2(s)H3(s)H2(s)R(s)C(s)N(s)E(S)G1(s)G3(s)H1(s)G2(s)H3(s)H2(s)R(s)C(s)N(s)E(S)P1=1△1=1+G2H2P1△1=?E(s)=1+G2H2+G1G2H3-G1H1G2H2-G1H1(–G2H3)R(s)[]N(s)(1+G2H2)(-G3G2H3)++R(s)E(S)G1(s)G3(s)H1(s)G2(s)H3(s)H2(s)C(s)N(s)R(s)E(S)G3(s)G2(s)H3(s)E(S)R(s)G1(s)H1(s)H2(s)C(s)P2=-G3G2H3△2=1P2△2=?梅逊公式求E(s)P1=–G2H3△1=1N(s)G1(s)H1(s)H2(s)C(s)G3(s)G2(s)H3(s)R(s)E(S)83 小　　结学习了描述线性定常系统的各种数学模型：微分方程、传递函数、动态结构图、信号流图以及脉冲响应函数。通过本章的学习，应能列写控制系统常用元件的数学模型和系统的数学模型；应牢固掌握绘制系统的结构图以及用结构图求闭环系统传递函数的方法。84'