直线与圆的位置关系教学课件PPT共三套.ppt 33页

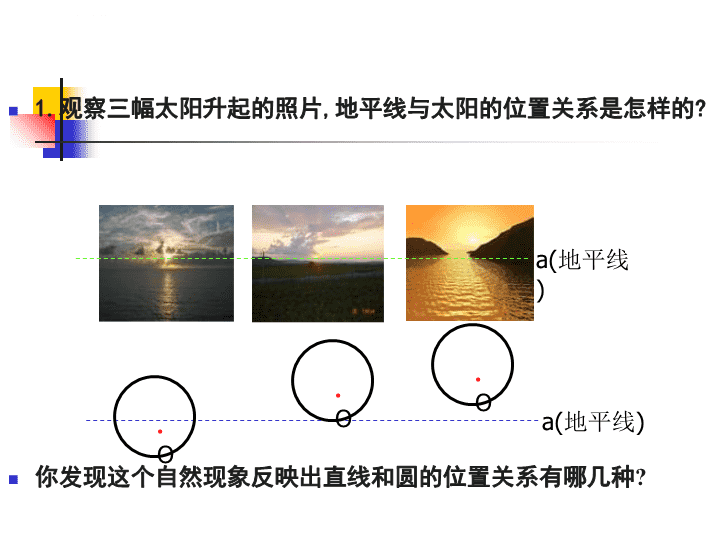
'3.1直线与圆的位置关系 海上日出 1.观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?a(地平线)a(地平线)●O●O●O 2.观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的?你发现这个自然现象反映出直线和圆的位置关系有哪几种?a(地平线)a(地平线)●O●O●O 直线与圆的位置关系作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,直线和圆有哪几种位置关系?●O●O有三种位置关系:相交直线和圆有惟一公共点(即直线和圆相切)时,这条直线叫做圆的切线,这个惟一的公共点叫做切点.●O相切相离直线与圆的交点个数可判定它们关系 做一做如图.O为直线L外一点,OT⊥L,且OT=d.请以O为圆心,分别以为半径画圆.所画的圆与直线l有什么位置关系?LTOdLTOdLTOd 如图,圆心O到直线l的距离d与⊙O的半径r的大小有什么关系?你能根据d与r的大小关系确定直线与圆的位置关系吗?●O●O相交●O相切相离直线与圆的位置关系量化rrr┐dd┐d┐ 直线和圆相交dr;dr;直线和圆相切直线和圆相离dr;直线与圆的位置关系量化●O●O相交●O相切相离rrr┐dd┐d┐<=> 练一练1.设⊙O的半径为r,圆心O到直线L的距离为d,根据下列条件判断直线L与⊙O的位置关系:d=4,r=3(2)d=1,r=(3)(4)2.在直角三角形ABC中,∠ACB=90°,CA=3,CB=4.设⊙C的半径为r.请根据r的下列值,判断AB与⊙C的位置关系,并说明理由.(1)r=2(2)r=2.4(3)r=3 1.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.以点C为圆心作圆,当半径为多长时,AB与⊙C相切?ACB┐D┛例1； 1、船有无触礁的危险如图,海中有一个小岛P,该岛四周12海里内暗礁.今有货轮四由西向东航行,开始在A点观测P在北偏东600处,行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行.要解决这个问题,我们可以将其数学化,如图:请与同伴交流你是怎么想的?怎么去做?你认为货轮继续向东航行途中会有触礁的危险吗?PABH北例2；600450 你说我说大家说下课了!学到了什么?还有什么疑惑与不解? 直线和圆的位置关系直线和圆的位置相交相切相离图形公共点个数圆心到直线距离d与半径r的关系公共点名称直线名称210dr交点切点无割线切线无O•drOl•drO•dr 3.1直线与圆的位置关系（2） 请按照下述步骤作图：在⊙O上任取一点A，连结OA。过点A作直线l⊥OAO问题：（1）圆心O到直线l的距离和圆的半径有什么关系？（2）直线l与⊙O的位置有什么关系？根据什么？（3）由此你发现了什么？ 直线与圆相切的判定定理：经过半径的外端并且垂直这条半径的直线是圆的切线。 做一做：(1)如图，AB是⊙O的直径，请分别过点A,B作⊙O的切线。OAB(2)如图，点Q在⊙O上。分别根据下列条件，判定直线PQ与⊙O是否相切：OPQ①OQ=6,OP=10,PQ=8②∠O=67.3°,∠P=22°42′ 例1：已知：如图，A是⊙O外一点，AO的延长线交⊙O于点C，点B在圆上，且AB=BC，∠A＝30°。求证：直线AB是⊙O的切线。OCBA 例2：如图，台风中心P（100，200）沿北偏东30°移动，受台风影响区域的半径为200km，那么下列城市A(200,300)，B(600,480)，C(550,300)，D(370,540)中，哪些受到这次台风的影响，哪些不受这次台风的影响？P北x(km)y(km)O100100ADBC OABCD练一练：已知：如图，AB是圆的直径，BC⊥AB，弦AD∥OC。求证：DC是⊙O的切线。 探究活动：课本第53页 3.1直线与圆的位置关系(2) 直线和圆的位置关系：ld＜rd=rd＞r相交相切相离 l请按照下述步骤作图:如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA。OA(1)圆心O到直线l的距离和圆的半径有什么关系?(2)直线l和⊙O的位置有什么关系?根据什么?(3)由此你发现怎样的直线是切线?经过半径的外端并且垂直这条半径的直线是圆的切线。切线的判定定理： 经过半径的外端并且垂直这条半径的直线是圆的切线。半径的外端垂直这条半径 例1:已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC，∠A=30°。求证：直线AB是⊙O的切线ABCO经过半径的外端并且垂直这条半径的直线是圆的切线 做一做：如图，已知点B在⊙O上。根据下列条件，能否判定直线AB和⊙O相切？⑴OB=6,AO=10,AB=8⑵∠O=68.5°,∠A=21°30′经过半径的外端并且垂直这条半径的直线是圆的切线 做一做：如图AB是⊙Ｏ的直径，请分别过A，B作⊙Ｏ的切线．ＡOB 例2：如图,台风P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200km,那么下列城市(200,380),B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到台风的影响?0100400500600700300200X(km)y(km)60050040030020010030°PABCD OPSTQ做一做：如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于S点。(1)过点P作⊙O的切线.(2)过点P的切线交OT于Q,判断S是不是OQ的中点,并说明理由. 1、切线的判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线。本节小结3、学会过圆上一点画切线.2、证明切线时常用的辅助线：作半径lOA 探究活动：请任意画一个圆,并在这个圆所在的平面内任意取一点P.(1)过点P是否都能作这个圆的切线?(2)点P在什么位置时,能作并且只能作一条切线?(3)点P在什么位置时,能作两条切线?这两条切线有什么特性?(4)能作多于2条的切线吗? 体会.分享说能出你这节课的收获和体验让大家与你分享吗？'