华东理工高等数学(上)11学分课件PPT-2.1 导数的概念.ppt 31页

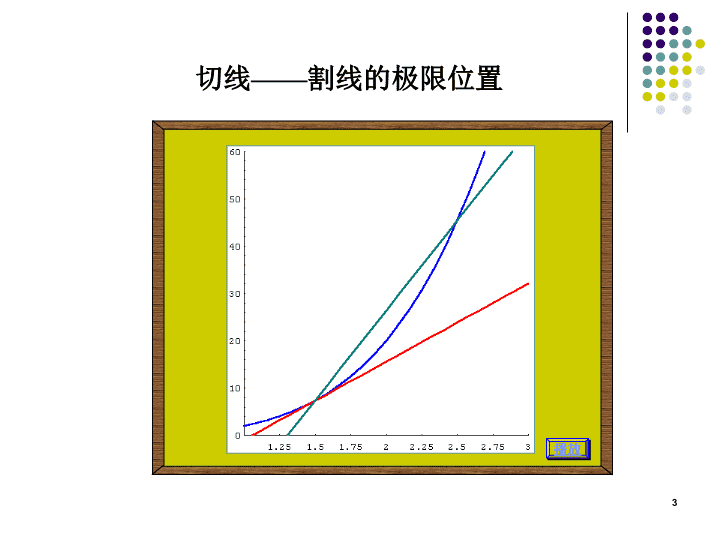
'第二章微积分学的创始人:德国数学家Leibniz微分学导数描述函数变化快慢微分描述函数变化程度都是描述物质运动的工具(从微观上研究函数)导数与极限导数思想最早由法国数学家Ferma在研究极值问题中提出.英国数学家Newton 2.1导数概念2.1.1引例A.切线问题圆的切线椭圆的切线？推广讨论曲线在点处的切线定义及其求法。2 切线——割线的极限位置播放3 切线——割线的极限位置4 切线——割线的极限位置5 切线——割线的极限位置6 切线——割线的极限位置7 切线——割线的极限位置8 切线——割线的极限位置9 切线——割线的极限位置10 切线——割线的极限位置11 切线——割线的极限位置12 切线——割线的极限位置13 如图,如果割线MN上点N沿曲线C无限趋于点M,则割线MN的极限位置直线MT称为曲线C在点M处的切线.极限位置即14 如果能求出曲线y=f(x)在点(x0,f(x0))处切线的斜率k,则曲线在点(x0,f(x0))处的切线方程为:例：求曲线在点处的切线，其中由的任意性可得曲线上任一点处的切线斜率为15 例：讨论曲线y=|x|在原点O(0,0)处的切线。注意：并不是一条曲线上任一点处总有切线。yOxQ2Q1y=|x|16 B.变速直线运动物体的速度设s=s(t)为物体沿直线运动的运动方程，求物体在时刻t0的瞬时速v(t0)。对于非匀速直线运动物体,(2)当tt0时,(1)先求出时刻t0到时刻t的平均速度:应趋于时刻t0的瞬时速度v(t0)17 18 2.1.2导数概念A.导数的定义定义设函数y=f(x)在给定点x0的某个邻域N(x0)内有定义,对该邻域内的任一点x(xx0),当自变量由x0变到x时,(记自变量增量△x=xx0)对应函数值的增量：△y=f(x)f(x0)或△y=f(x0+△x)f(x0)则称函数f(x)在点x0处可导.19 并称此极限为f(x)在点x0处的导数,记为f(x0),f(x0)也可记为:20 如果如果f(x)在(a,b)内的每一点都可导,此时称f(x)在(a,b)内可导,此时对于(a,b)内的任一点x,都存在导数f(x),这样得到一个新的函数,称为f(x)的导函数,则称f(x)在点x0处不可导。记作f(x).21 22 B.导数的几何意义：导数在物理方面的意义：yxOx0y=f(x)TMNf(x0)表示曲线y=f(x)在点(x0,f(x0))处切线MT的斜率,(1)变速直线运动物体的运动方程为:s=s(t)则s(t0)速度表示瞬时速度v(t0)。(2)若Q(t)表示通过导体横截面的电量,则Q(t0)表示时刻t0通过导体横截面的电流强度。k=tan,即,f(x0)=tan.23 24 例1.求常数函数f(x)=C的导数f(x).解：即,(C)=0.过点且与切线垂直的直线称为曲线在该点处的法线。当时，法线斜率法线方程当时，法线方程25 26 27 C.函数的增加率28 29 牛顿(1642–1727)伟大的英国数学家,物理学家,天文学家和自然科学家.他在数学上的卓越贡献是创立了微积分.1665年他提出正流数(微分)术,次年又提出反流数(积分)术,并于1671年完成《流数术与无穷级数》一书(1736年出版).他还著有《自然哲学的数学原理》和《广义算术》等. 莱布尼兹(1646–1716)德国数学家,哲学家.他和牛顿同为微积分的创始人,他在《学艺》杂志上发表的几篇有关微积分学的论文中,有的早于牛顿,所用微积分符号也远远优于牛顿.他还设计了作乘法的计算机,系统地阐述二进制计数法,并把它与中国的八卦联系起来.'