最新26.1.7-二次函数与一元二次方程、不等式的关系课件课件PPT.ppt 78页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。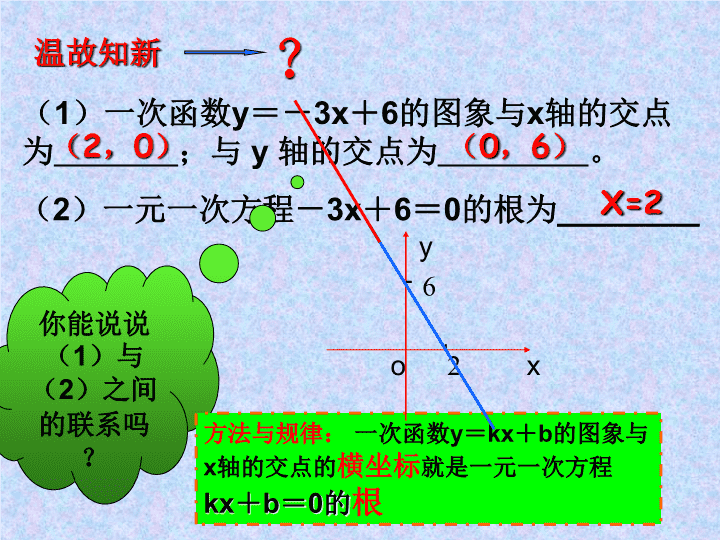　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅26.1.7-二次函数与一元二次方程、不等式的关系课件 温故知新（1）一次函数y＝－3x＋6的图象与x轴的交点为；与y轴的交点为。？（2，0）（2）一元一次方程－3x＋6＝0的根为________（0，6）X=2你能说说（1）与（2）之间的联系吗？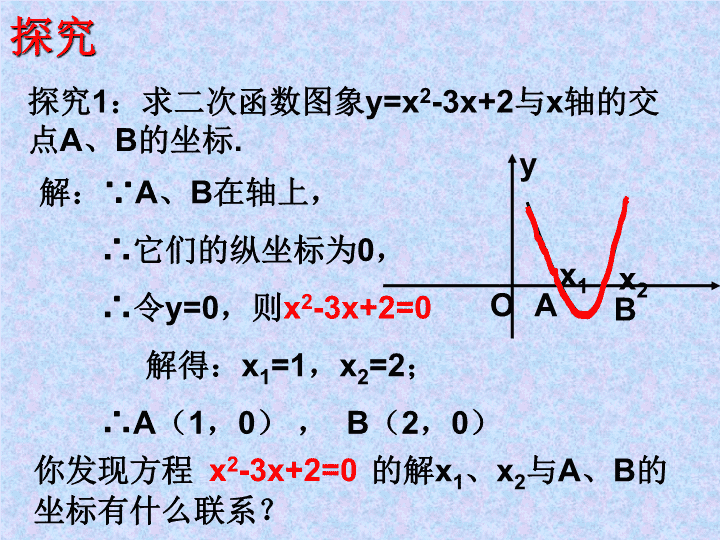方法与规律：一次函数y＝kx＋b的图象与x轴的交点的横坐标就是一元一次方程kx＋b＝0的根2xyo6 探究探究1：求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标.解：∵A、B在轴上，∴它们的纵坐标为0，∴令y=0，则x2-3x+2=0解得：x1=1，x2=2；∴A（1，0），B（2，0）你发现方程的解x1、x2与A、B的坐标有什么联系？x2-3x+2=0OABx1x2y 简单运用 1.已知抛物线y=2x2+bx+8的顶点在x轴上，则b=。2.若二次函数y=（m-8）x2+2x+m2-64的图象过原点，则m=。±8-8二、基础训练3.根据下列表格的对应值：判断方程ax2+bx+c=0（a≠0,a、b、c为常数）一个解的范围是　（　　　　）Ａ、3＜x＜3.23Ｂ、3.23＜x＜3.24Ｃ、3.24＜x＜3.25Ｄ、3.25＜x＜3.26x3.233.243.253.26y=ax2+bx+c-0.06-0.020.030.09C 二、基础训练4.已知抛物线y=x2-6x+a的顶点在x轴上，则a；若抛物线与x轴有两个交点，则a；若抛物线与坐标轴有两个公共点，则a；6.已知抛物线y=x2+px+q与x轴的两个交点为（-2，0），（3，0），则p=___，q=__5.已知抛物线y=x2-3x+a+1与x轴至少有一个交点，则a的范围是。 三、拓展应用练习1.已知二次函数y=（k﹣3）x2+2x+1的图象与x轴有交点，则k的取值范围是（）A、k＜4B、k≤4C、k＜4且k≠3D、k≤4且k≠3D 练习2.关于x的二次函数y=(k-1)x2-3x-1的图像全部位于x轴的下方，则k的取值范围是；k＜-5/4知识小结：(1)抛物线y=ax2+bx+c全部在x轴上方的条件：a__0,b2-4ac__0；(2)全部在x轴下方的条件：a__0,b2-4ac__0＞＜＜＜ .已知二次函数的图像与X轴有两个不同的交点.（1）求k的取值范围（2）当k为何值时，这两个交点横坐标的平方和等于50.能力提升解：△=∵＞0∴k的取值为解：解之得：k的取值为∴ 要点小结一般地，关于x的一元二次方程ax2+bx+c=0(a≠0)的根就是二次函数y=ax2+bx+c(a≠0)的值为0时自变量x的值，也就是函数y=ax2+bx+c的图象与x轴交点的横坐标。可由一元二次方程的根的判别式来判定二次函数图象与x轴的交点的情况，由根与系数的关系来解决相关问题。在函数问题中，往往需要解方程：反过来也可以利用函数图象解方程。 三、课后习题已知二次函数y=x2-kx+k-2.(1)求证:不论k取何值时，这个二次函数y=x2-kx+k-2与x轴有两个不同的交点。(2)如果二次函数y=x2-kx+k-2与轴两个交点为A、B，设此抛物线与y轴的交点为C，当k为6时,求S△ABC. 四、小结1、若一元二次方程ax2+bx+c=0的两个根是x1、x2，则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A（x1，0），B（x2，0）2、若一元二次方程ax2+bx+c=0与二次函数y=ax2+bx+c之间的互相转化的关系。体现了数形结合的思想。 当x取何值时，y＜0？当x取何值时，y＞0？能否用含有x的不等式来描述两个问题？探究三：你的图象与x轴的交点坐标是什么？xyy＝x2－2x－3根据图象回答下列问题． 例题精讲3.已知二次函数y=-x2+3x+4的图象如图；(1)方程-x2+3x+4=0的解是_____(2)不等式-x2+3x+4>0的解集是____(3)不等式-x2+3x+4<0的解集是___xyo12345-1-21234-1-2-3-4-5x=-1,x=4X<-1或x>4-10,y=0,y<00x1x2xy当x=x1或x=x2时,y=0当xx2时,y<0当x10xyx1x2Oxyx1x2当x=x1或x=x2时,y=0当xx2时,y>0当x10,y=0,y<0y≥2 ⊿=b2-4acy=ax2+bx+c（a>0）图像ax2+bx+c=0（a≠0）的根ax2+bx+c>0（a>0）解集ax2+bx+c<0（a>0）解集X2X1xy0OxX1=X2xyxOxy⊿>0⊿＝0⊿＜0x1＝x2x1=x2＝－b/2a没有实数根xx2x≠x1的一切实数所有实数x1①-x2+x+2=0;②-x2+x+2>0;③-x2+x+2<0.<2>①x2-4x+4=0;②x2-4x+4>0;③x2-4x+4<0.<3>①-x2+x-2=0;②-x2+x-2>0;③-x2+x-2<0.Xy02Oxy-12Xy0y=-x2+x+2 拓广：函数y=ax2+bx+c的图像如图，那么1）方程ax2+bx+c=2的根是__________;2）不等式ax2+bx+c>2的解集是_________;3）不等式ax2+bx+c<2的解集是_________;3-1Oxy2(4,2)(-2,2)X1=-2;X2=4X<-2;X>4-2