最新《推理能力培养》PPT课件PPT课件.ppt 93页

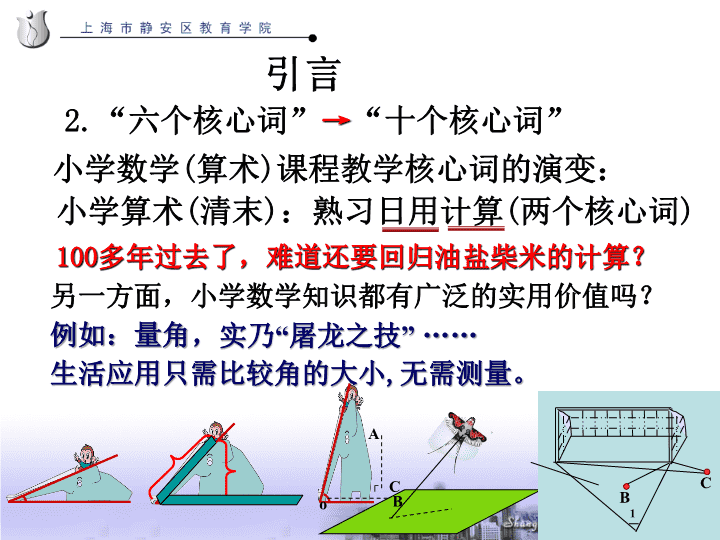
'《推理能力培养》PPT课件 引言教育部义务教育数学课程标准（2011年版）最大的改变：1.“双基”→“四基”数学的基础知识、基本技能、基本思想、基本活动经验意味着：我国数学教育优良传统得到肯定理解＋记忆；回归“结果”与“过程”并重的理念铺垫＋变式……“但求曾经拥有，不求天长地久”…… 引言2.“六个核心词”→“十个核心词”小学数学(算术)课程教学核心词的演变：小学算术(清末)：熟习日用计算(两个核心词)100多年过去了，难道还要回归油盐柴米的计算？另一方面，小学数学知识都有广泛的实用价值吗？例如：量角生活应用只需比较角的大小,无需测量。，实乃“屠龙之技”……┌oBC1CAB 基于核心词的能力架构空间观念数据分析观念运算能力数学建模核心词十个之多，还有核心吗？说明研究尚处初级阶段，缺乏概括，有待更深入、更浅出！推理能力AB 一、什么是推理推理：由已知判断推出未知判断的思维。(前提)(结论)它的本质是从已有知识得到新知识,特别是可以得到不可能通过感觉经验掌握的新知识。例如：起初人们认为线段长度总能用整数或分数表示。希腊数学家希帕斯通过推理得出边长为1的正方形，它的对角线不能用分数表示。这一伟大的发现，促使人们从依靠直观、经验转向重视推理论证。11 一、什么是推理推理的形式具有多样性。例如：①已知“小明哥哥已大学毕业”“小明受教同一老师”,推出“小明也能大学毕业”。②已知“一千只苹果是红的”，推出“苹果都是红的”。③已知“太平洋已被污染”，“大西洋已被污染”，“印度洋已被污染”，“北冰洋已被污染”，推出“地球上所有大洋都已被污染”。④已知“人终将一死”“约翰是人”推出“约翰会死”。类比不完全归纳完全归纳演绎 一、什么是推理又如：①已知“长方形面积＝长×宽”“长、宽是长方形邻边”,推出“平行四边形面积＝邻边相乘”。②已知“”，推出“”。③已知“袋里有5个球”“摸出第1、2、3个都是红的”推出“袋里全是红球”。④已知“1＋3＝22,1＋3＋5＝32,1＋3＋5＋7＝42”,推出“从1起连续奇数的和等于奇数个数的平方”。类比不完全归纳类比不完全归纳×?√√推理的形式具有多样性。 一、什么是推理推理的形式具有多样性。又如：①已知“2，3，5，7都不能整除29”,推出“29是质数”。②已知“平行四边形面积＝底×高”，“任何两个全等三角形能拼成一个平行四边形,且三角形的底和高就是平行四边形的底和高”,推出“三角形面积＝底×高÷2”。完全归纳演绎√√ “类比”是由特殊到特殊的推理；“归纳”是由特殊到一般的推理；“演绎”是由一般到特殊的推理。一、什么是推理推理的形式具有多样性。 一般地说，推理可以分为：推理类比推理归纳推理演绎推理不完全归纳推理完全归纳推理或然推理必然推理必然推理主要指演绎推理；或然推理又叫做合情推理（似真推理），是一种合乎情理的、好像为真的推理。一、什么是推理 1.心理学视角的描述“数学推理能力”：在数学活动中，运用合情推理去理解数学概念、公式、法则或获得发现、得出猜想，并用演绎推理对发现、猜想加以检验、证明的个性心理特征。推理能力的发展应贯穿于整个数学学习过程中。推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。——数学课程标准(2011年版)二、什么是数学推理能力 2.数学课程标准的阐述推理一般包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果；演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算。——数学课程标准(2011年版)二、什么是数学推理能力 3.两类推理相辅相成的必要性演绎推理只能证明，而不能发现真理。传统的数学教学缺少：通过条件预测结果的能力、依据结论探究成因的能力。缺少这两个能力就难有真正的创造，也不利于创新型人才的成长。预测、探究的事物事先并不确切知道，所以无法借助演绎推理完成。二、什么是数学推理能力 3.两类推理相辅相成的必要性在解决问题的过程中，两种推理功能不同，相辅相成：合情推理用于探索思路，发现结论；演绎推理用于证明结论。——数学课程标准(2011年版)二、什么是数学推理能力 三、小学数学中的推理1.演绎推理举例黑、灰、白三只兔子赛跑。黑兔说：“我不是最快的，但比白兔快。”请问，谁跑得最快?谁跑得最慢?∵黑兔不是最快，白兔不是最快∴灰兔最快（排除法）计算7＋5＝？∵7＋3＝10；10＋2＝12∴7＋5＝7＋3＋2＝10＋2＝12直角三角形的一个锐角是30°,另一个锐角是多少？∵三角形内角和＝180°∴另一个锐角是180°－90°－30°＝60° 三、小学数学中的推理2.演绎推理课例分析并非教学速度概念：为正式引进速度概念奠定更好的认知基础解决问题（实际应用问题）识别信息→说明依据跳出了“多样化”与“优化”的争论“特殊方法”与“一般方法”互补打字人小亚小巧小丁丁总字数174192192时间(分)668→提出问题→解决问题→交流解法 三、小学数学中的推理深入挖掘了常规问题的数学推理内涵①巧＞亚②巧＞丁③亚＞丁（时间相同，打字多的快）（字数相同，时间少的快）（字数、时间都不同，每分钟打的多快）打字人小亚小巧小丁丁总字数174192192时间(分)6682.演绎推理课例分析 三、小学数学中的推理2.演绎推理课例分析深入挖掘了常规问题的演绎推理内涵①巧＞亚②巧＞丁③亚＞丁巧最快丁最慢完全归纳由①③：巧＞亚＞丁传递反过来：丁＜亚＜巧逆反演绎打字人小亚小巧小丁丁总字数174192192时间(分)668 6346商13乘1减落由具体的算例：如：46÷3＝？……归纳得出：整数除法计算法则。由三条线段围成三角形的操作，归纳得出：三角形任意两边之和大于第三边。由摸棋实验，归纳推断：红棋比白棋多，两种棋约占总数的几分之几。三、小学数学中的推理3.合情推理举例 三、小学数学中的推理3.合情推理举例由除法的基本性质：被除数、除数都乘或除以相同的数(0除外)商不变类比推出分数、比的基本性质：分数的分子、分母都乘或除以相同的数(0除外)分数的大小不变。……由整数乘法计算类比推出小数乘法计算：如：0.15×3＝？0.15×3450.11 四、合情推理与演绎推理怎样相结合因为3×6＝18所以30×600＝18000凭借经验和直觉—合情推理因为3×6＝18所以30×6＝18个十所以30×600＝180个百凭借整数的概念—演绎推理＝180＝18000末尾有0的乘法：1.计算教学实例 四、合情推理与演绎推理怎样相结合因为长方形面积＝长×宽所以长方体体积＝长×宽×高类比—合情推理根据体积单位概念与计数—演绎计算长方体的体积：2.几何教学实例 四、合情推理与演绎推理怎样相结合2.几何教学实例周长与表面积计算：将二维空间观念推广到三维空间观念凭借几何直观猜想：与正方形周长相等—合情推理通过平移转，验证、说明猜想的正确性—演绎推理合情推理→演绎推理 1.充分利用直观很多情况下，数学的结果是“看”出来的，“看”是一种直观判断，即数学的直觉智慧。2.鼓励学生猜想以事实、经验为基础，由此及彼，发现问题、提出问题，大胆“假设”。3.启发学生说理以所学数学概念、性质、法则、公式为依据，说明猜想，解释结论。五、怎样培养小学生的推理能力 五、怎样培养小学生的推理能力4.数、形、事结合采用多种方式辅助说理：“算理”＋“事理”＋“图示”。多渠道地促进理解与表达。 “算理＋事理＋图示”的实例——乘法分配律 “算理＋事理＋图示”的实例——乘法分配律【复习引入】我们已学：加法交换律，结合律；……那么，加法和乘法之间有什么运算规律呢？【尝试与发现】（12＋8）×6=12×6＋8×6=它们是得数相等的两个算式，可以用等号连起来：（＋）×=×＋×。再写出几个这样的算式：（＋）×=×＋×；……你发现了什么规律？能总结吗？有困难看课本。 “算理＋事理＋图示”的实例——乘法分配律【验证与理解】一个长方形操场，原来长65米，宽32米。扩建后长不变，宽增加15米，现在操场面积有多大？看作一个长方形求：；看做两个长方形求：。算法不同，结果。所以：(＋)×=×＋×。编一道这样的实际问题：？用乘法意义说明：如：(12＋8)×6=12×6＋8×6表示一共有个6＝个6加个6。原来面积增加面积653215 五、怎样培养小学生的推理能力5.适当开展推理训练首先是结合基础知识的教学实施训练。例1由相交引出垂直：如图，量得一个角是直角，∠1＝()；∠2＝()。其次是结合平时的教学穿插训练。12 五、怎样培养小学生的推理能力5.适当开展推理训练例2看图推理：最重；最轻。例3找规律推理：112梯形个数12345…10周长(cm)581114… 6.培养良好的思维习惯最主要的是：有根有据；有条有理。推理能力的发展与语言的发展，关系密切，两者是相互促进的。发展小学生的推理能力，就要提高学生用数学语言合乎逻辑地进行讨论和质疑的能力。五、怎样培养小学生的推理能力 7.提高教师自身的数学素养练习：五、怎样培养小学生的推理能力（1）有学生发现：1×2×3×4＋1＝(1×4＋1)2＝(2×3－1)22×3×4×5＋1＝(2×5＋1)2＝(3×4－1)23×4×5×6＋1＝(3×6＋1)2＝(4×5－1)2……连续四个自然数的积加1等于头尾两数的积加1和的平方，等于中间两数的积减1差的平方。这一规律成立吗?请给以证明。 7.提高教师自身的数学素养练习：五、怎样培养小学生的推理能力（2）有学生说，推导梯形面积计算公式，可以延长两腰相交成大三角形，然后大三角形面积减去小三角形面积，就是梯形面积。请完整写出这一思路的推导过程。┐ABCDE 7.提高教师自身的数学素养练习：五、怎样培养小学生的推理能力（1）设四个连续自然数为n－1，n，n＋1，n＋2，则所以，学生发现的规律成立。 7.提高教师自身的数学素养五、怎样培养小学生的推理能力┐ABCDE作DF∥CB交于AB的延长线于F，则BCDF为□，AF为梯形ABCD上、下底的差.连接DB，连接FE，则三角形AFE的面积为设小三角形高为l.BADCEF┐,即 1.数学模型与建模六、关于数学建模数学模型是用数学符号、式子、程序、图形等对实际课题本质属性的抽象而又简洁的刻划。它能解释某些客观现象，或预测未来的发展规律，或为控制某一现象的发展提供最优策略或较好策略。从实际课题中抽象、提炼出数学模型的过程就称为数学建模。调研→假设→建立→求解→分析→检验→应用 2.模型思想六、关于数学建模“模型”是所研究的系统、过程、事物或概念的一种表达形式。“模型思想”与“建模思想”的区别可理解为：模型思想是初步的、大致的建模思想；模型思想比数学建模有更广泛的内涵。 2.模型思想模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义。这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识。——数学课程标准(2011年版)六、关于数学建模 六、关于数学建模3.小学数学中的数学模型常见数量关系；计算公式等都是典型的数学模型。如：单价×数量＝总价S＝ab又如：水池同时打开进水管、出水管……几小时后水池满？动态平衡的数学模型只是“取材不当” 六、关于数学建模4.小学数学中的数学建模小胖每分走40米，小巧每分走60米，他们从相距1500米两地同时出发相向而行，几分钟相遇？师徒共做1540个零件。徒弟做了16天,平均每天做40个；师傅做了15天,平均每天做几个？买15个足球、16个篮球，足球每只60元，篮球每只40元，一共应付多少元?如图,求两种蔬菜的面积(单位:米)。a×b＋c×d＝s1500÷(40＋60)(1540－40×16)÷1560×15＋40×16＝1540青菜韭菜6040161540x＋60x＝150040×16＋15x＝1540设x分相遇，设每天x个， 六、关于数学建模4.小学数学中的数学建模a×b＋c×d＝s 六、关于数学建模5.用数学建模思想反思某些一题多解小胖每分走40米，小巧每分走60米，他们从相距1500米的两地同时出发，相向而行，几分钟后相遇？ab＋cd＝s40x＋60x＝15001500－40x＝60x1500－60x＝40x(60＋40)x＝15001500÷x＝60＋401500÷x－40＝601500÷x－60＝401500＝40x＋60x60x＝1500－40x40x＝1500－60x这样的一题多解有意义吗？你认为怎样列方程便于思考?设x分钟后两人相遇。………… 六、关于数学建模6.正确处理建模思想与策略多样化的关系2元、5元人民币共15张，共54元。2元、5元各几张？列表；画图；推算；列方程假设：15张全是5元，共5×15＝75(元)比较：调整：（置换）列表尝试，实质上是连续多次：假设→比较→调整2元(张)05元(张)15总价(元)………785411472每次减少3元，21369755－275－54＝21(元)21÷()列方程解：x＋y＝152x＋5y＝542x＋5(15-x)＝54化难为易 谢谢！欢迎提问共同探讨聚焦小学数学的核心能力 疟疾昆明医学院附属第二医院 疟疾（malaria)：人体疟原虫经按蚊媒介传播的常见寄生虫病。疟原虫肝细胞发育繁殖红细胞内寄生增殖红细胞周期性大批破坏发病。临床特征：周期性定时发作的寒战、高热、出汗、退热，可多次反复发作，久则出现贫血和脾肿；恶性疟还能引起严重的、甚至致命的凶险发作。血 【病原学】人体疟原虫分四种:间日疟原虫、恶性疟原虫、三日疟原虫、及卵形疟原虫。疟原虫生活史包括两个阶段：人体内无性增殖按蚊体内有性增殖 传染性按蚊吮吸病人的血时：子孢子随按蚊的唾液人体血液约经30分钟，血肝细胞转变成圆形核分裂（无性的裂体生殖）恶性疟原虫5～6天，间日疟8天卵形疟9天，三日疟11～12天裂殖体成熟放出1.2～4万个裂殖子一部分被巨噬细胞吞噬一部分侵入红细胞，进行裂体增殖，引起临床发作 间日疟原虫子孢子进入肝细胞后,在发育繁殖速度上可能是多态的：速发型子孢子迟发型子孢子休眠子：不发育的原虫这些子孢子都是不同质的。因此在肝细胞内发育繁殖，也不是完全同步的，有快有慢。这是间日疟潜伏期有长有短，复发有近期、有远期的原因。 红细胞内原虫环状体、晚期滋养休、裂殖体各阶段裂殖子红细胞破裂释出裂殖子继续侵犯其他红细胞，继续无性增殖。经过几代增殖后，一部分原虫发育配子体按蚊蛰人随血液蚊胃配子雌雄配子结合合子动合子胃壁外层囊合子成熟后孢子囊（内含许多孢子体逸出，穿过体腔入于涎腺，待机输入人体） 蚊体内：有性增殖人体内：无性增殖发病 恶性疟骨髓象（集中视野）1环状体2滋养体3裂殖体前期4雄配子体5雌配子体6早幼粒细胞7晚幼红细胞 三日疟血象（集中视野）1环状体2滋养体3裂殖体4雄配子体5雌配子体6中性分裂核粒细胞7淋巴细胞 间日疟血象1环状体2滋养体3裂殖体4雄配子体5雌配子体6中性分裂核粒细胞7淋巴细胞 【流行病学】传染源：疟疾患者和带疟原虫者传播途径：按蚊叮咬皮肤，少数为输血平原区间日疟：中华按蚊山区：微小按蚊丘陵地区：雷氏按蚊海南山林地区：大劣按蚊 【流行病学】传染源：疟疾患者和带疟原虫者传播途径：按蚊叮咬皮肤，少数为输血人群易感性：感染后有一定免疫力，但不持久各型疟原虫之间无交叉免疫反复多次感染 【流行病学】传染源：疟疾患者和带疟原虫者传播途径：按蚊叮咬皮肤少数为输血人群易感性：流行特征：热带＞亚热带＞温带流行区以间日疟最广，恶性疟最严重季节多以夏秋季较多。 【发病机制】红内期一般无症状。红细胞破裂释放出裂殖子同时，伴随诱生多种细胞因子及代谢产物入血寒战、高热继之大汗的典型症状。症状的严重程度主要取决于原虫血症的数量。疟原虫生活史的两个特点：繁殖周期中产生巨大量的子代抗原的多样性疟原虫能够在宿主体内较长期存在，并在自然界持续传播 【临床表现】平均潜伏期：间日疟、卵形疟14天，三日疟30天，恶性疟12天典型发作：慢性疟疾：再燃与复发：由迟发型子孢子所引起特殊类型疟疾：间日疟三日疟卵形疟恶性疟 间日疟多数起病急骤，尤其是复发患者。初发时可有低热、乏力、头痛、食欲减退等前驱症状。初起发热大多不规则，数天后转为周期性和间歇性发作。典型发作可分为三期:123 发冷期：骤然发冷、剧烈寒战、口唇青紫、皮肤苍白或微带青紫色，脉细速，血压升高初觉寒冷，体温通常<38℃；到发冷期末，可以升达39～40℃初发患者，此期持续约10～15分钟，反复发作后，则此期可渐增长达30～45分钟。 发热期：寒战停止高热升达39.5～41℃颜面潮红，脉搏洪速，头痛如裂，全身肌肉、关节疼痛，口干烦渴，甚至谵妄严重者，可发生抽搐及昏迷一般持续2～6小时。 出汗期：盛汗退热，衣褥尽湿病人感觉舒适，但十分困倦此期约2～3小时血象：WBC及NC在急性发作时可增加，发作过后则正常多次发作后，则WBC减少而MC增多 规律性：整个典型发作全程约6～10小时，间歇期无症状典型者常48小时发作一次尤其是在复发时明显影响因素：二组或二组以上不同发育周期的虫株或高疟区病人可能有不同种类的疟原虫的混合感染，可每日发作，或呈不规则的发作疟疾后期免疫力增加，或治疗不充分等，均能影响发作的规律性 三日疟：多无前驱症状发作周期多数是72小时(即3天一次)持续不变。发作时，发冷期、发热期和出汗期症状划分明显出汗期退热较速，故易引起虚脱脾肿及贫血轻，而蛋白尿则较常见病程长且复发率高，病程一般不超过三年。某些地区，儿童反复感染三日疟，可能发生肾病综合征，称为疟疾肾病。 卵形疟：前驱症状不明显常无恶寒、战栗，热度低，易自愈无明显贫血及脾大一般发作不到6次，就不再复发 恶性疟：前驱症状常见发作时可有畏寒，头痛、恶心、呕吐常见热型常不规则，一次发热可长达20～36小时或更长贫血及脾大出现早而明显初发5～10天后，无免疫力患者易演变为。凶险发作 脑型疟疾凶险发作类型过高热型胃肠型 凶险发作脑型：最多见症状类似脑炎及脑膜炎，表现为头痛、发热，不同程度的意识障碍，如未及时救治，则病情继续发展，导致脑水肿，呼吸、循环、肾功能衰竭，迅速死亡，病死率高达50%。其发生于受染的红细胞堵塞微血管、低血糖、细胞因子有关。进食不足、疟原虫发育消耗能量、奎宁治疗刺激胰岛素分泌 超高热型：体温迅速上升至42℃或更高，持续不退患者呼吸急促、烦躁不安、谵妄、昏迷，常伴发惊厥或抽搐，大小便失禁，皮肤约热干燥或呈青紫色可数小时内死亡 胃肠型：高热弛张、恶心呕吐、腹泻频繁，水样便或血便可伴里急后重、剧烈腹痛及结肠部压痛，无腹泻，常易误认为急腹症后期休克、急性肾衰：脉搏细弱、血压下降、皮肤厥冷、冷汗、体温下降，少尿或无尿 肺水肿型：患者骤发呼吸困难，明显发绀，口鼻涌出泡沫状血性分泌物。虽无过多输液，亦可发生。 慢性疟疾：以间日疟及三日疟为多常呈不规则低热，三期表现不明显，消瘦、乏力贫血加重脾脏肿大更明显且变坚硬。 孕妇疟疾先天性疟疾婴幼儿疟疾输血疟疾 【并发症】黑尿热（溶血尿毒综合征）疟疾性肾病DIC、心血管系统异常、黄疸及肝功能不全以及各种感染 黑尿热主要由于疟原虫感染、患者先天缺乏G-6-PD或其他红细胞酶有关诱因：奎宁和伯氨喹等抗疟药治疗急性血管内溶血，引起血尿及血红蛋白尿，严重者导致肾缺血及肾小管坏死起病急骤寒战高热、腰痛、呕吐、腹痛、尿量骤减，呈暗红色或黑色（酱油色）尿中出现白蛋白、管型、上皮细胞及血红蛋白。 疟疾性肾病急性肾功能衰竭：恶性疟反复发作，可出现进行性少尿和尿闭抗疟治疗和血透析治疗有效肾病综合征：三日疟长期反复发作后，表现为进行性蛋白尿、贫血与水肿为疟疾抗原抗体复合物沉积于肾小球毛细血管基底膜与血管间质所致抗疟药治疗在肾病早期可获明显效果，晚期效果差 【诊断】临床诊断：凡曾在有蚊季节去过疟疾流行区，或有疟疾病史、或有输血史的人发生原因未明的发热，或伴有进行性贫血及脾肿大，都应想到疟疾的可能性如有上述病史及现有典型发作过程，则可作出初步诊断。 实验诊断：1、原虫检查：确诊的根据，血涂片或划皮法采组织液涂片2、免疫学诊断：检测疟原虫抗原检测抗疟原虫的特异性抗体3、基因检测：DNA探针技术及PCR技术直接测原虫DNA4、治疗诊断法： 【鉴别诊断】与发热疾病鉴别：败血症、伤寒、钩端螺旋体、胆道感染、尿路感染等。脑型疟：应与乙脑、中毒性菌痢鉴别。黑尿热：应与阵发性血红蛋白尿症、蚕豆病鉴别。最重要的鉴别诊断方法：病原学的确定 【治疗】治疗原则：①应用抗疟药愈早愈好②适当选用抗疟药，要求安全、有效、简便易行a.在已发现耐氯喹虫株的地区，对重症及恶性疟患者，尽量避免采用氯喹b.对有溶血病史或红细胞缺乏G-6-PD的病人，忌用伯氨喹啉类药物。③力争根治，以免复发及转成慢性。④重视对症治疗与护理，尤其是凶险发作患者，更应注意。 一般治疗与对症治疗卧床休息，发冷期间注意保暖，高热时可予物理降温，酌予解热剂，多饮水，流质饮食；吐泻明显者可输液严重贫血者，可输血、铁剂及高蛋白饮食出现脑水肿或昏迷，及时积极脱水监测血糖，及时发现和纠正低血糖 病因治疗对氯喹敏感的疟疾发作治疗1、氯喹：磷酸氯奎首剂1g口服6~8h后再服0.5g第2、3日各再服0.5g＝总量2.5g2、伯氨喹：39.6mgQD,连服8天，控制复发 耐氯喹疟疾发作的治疗1、甲氟喹：750mg一次顿服2、磷酸咯萘啶：第一日0.4g两次口服，第2、3日各0.4g。3、青蒿素：首剂1g，第2、3日各0.5g。或蒿甲醚首剂300mgim,第2、3日各150mg以青蒿素为基本药物的联合治疗方法推荐首选 凶险型疟疾发作的治疗1、氯喹：用于敏感株的治疗，基质10mg/kgiv4h5mg/kgiv2h，总量＜25mg/kg2、奎宁：用于耐氯喹株感染，500mgiv4h，12h后可重复，清醒后改为口服3、磷酸咯萘啶：4、青蒿琥脂： 【预防】化学预防1、根治疟疾现症病人及带疟原虫者，健全疫情报告。间日疟：氯喹＋伯氨喹1～2年内疟疾史者：高峰前二月集体抗复发治疗，乙胺嘧啶8片连服2天，加伯氨喹2片连服8天。 2、预防性服药：高疟区健康人群及外来人群。（1）非耐氯喹疟疾流行区：首选氯喹，每周0.3g（2）耐氯喹疟疾流行区：甲氟喹每周0.25g 控制传播媒介清除按蚊幼虫滋生产所及广泛使用杀虫药。 疫苗预防研究发展包含各阶段疟原虫的主要抗原成分——理想疫苗 Byebye'