最新提公因式法分解因式ppt课件(1)课件PPT.ppt 58页

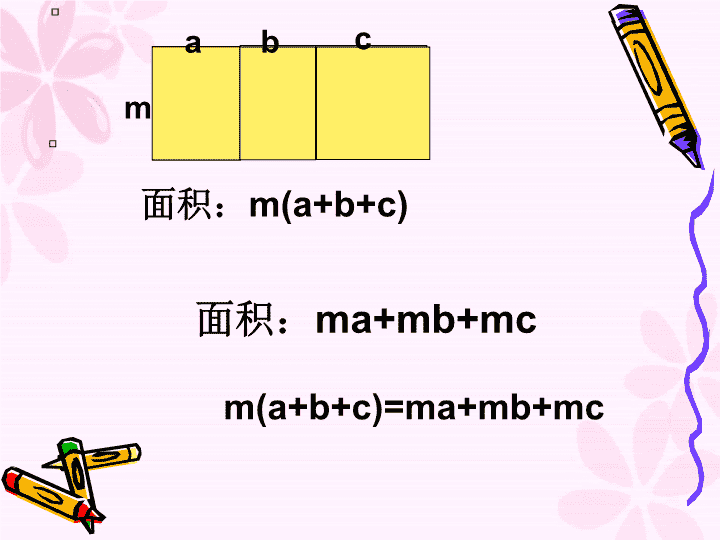
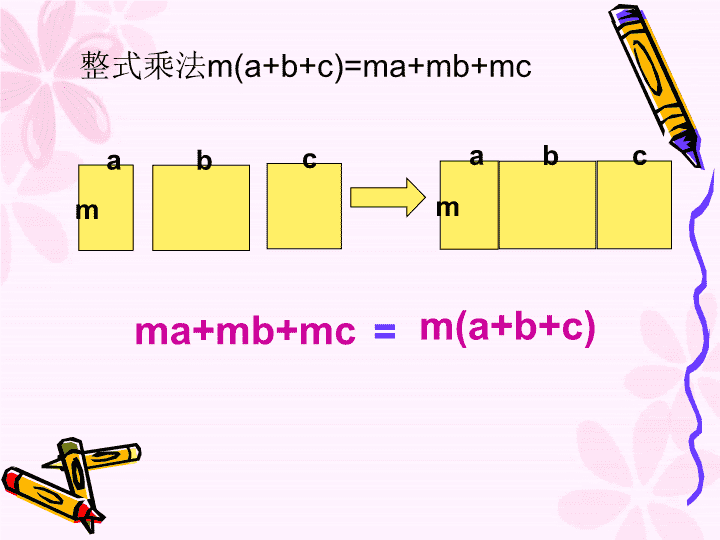
'提公因式法分解因式ppt课件(1) mabc面积：m(a+b+c)面积：ma+mb+mcm(a+b+c)=ma+mb+mc ambcma+mb+mcm(a+b+c)=整式乘法m(a+b+c)=ma+mb+mcambc 判断下列各式哪些是整式乘法?哪些是因式分解?(1)x2－4y2=(x+2y)(x－2y)(2)2x(x－3y)=2x2－6xy(3)(5a－1)2=25a2－10a+1(4)x2+4x+4=(x+2)2(5)(a－3)(a+3)=a2－9(6)m2－4=(m+2)(m－2)(7)2πR+2πr=2π(R+r).练习一理解概念因式分解整式乘法整式乘法因式分解整式乘法因式分解因式分解 ma+mb+mc因式分解整式乘法m(a+b+c)因式分解与整式乘法是相反方向的变形整式的乘法与因式分解有什么关系？类比与比较 下列从左到右的变形是分解因式的有()A.6x2y=3xy·2xB.a2－b2+1=(a+b)(a－b)+1C.a2－ab=a(a－b)D.(x+3)(x－3)=x2－9选择题C 温馨提示判断是否是因式分解要看等式的左边是否是一个多项式，右边是否是几个整式的积的形式。试一试：下列由左边到右边的变形中，哪些是因式分解，哪些不是？（1）（）（2）(x+2)(x-2）=x2-4（）（3）a2-b2+1=(a+b)(a-b)+1（）（4）ax2+ay2=a(x2+y2)（）（5）6x2y=3xy·2x（）是不是不是是不是 1、多项式ab+bc各项都含有相同的因式吗？多项式3x2+6x呢？多项式mb2+nb+b呢？2、你能将上面的多项式写成几个因式的乘积的形式？说明你的理由？ 多项式各项都含有的相同因式叫做这个多项式各项的公因式.如：bx+ax的公因式是ｘ． 因式分解：把公因式提出来，多项式ma+mb+mc就可以分解成两个因式m和(a+b+c)的乘积。像这种因式分解的方法，叫做提取公因式法。解:公因式提公因式法 例1:找出3x2–6x的公因式。并分解因式。系数：各项系数的最大公约数。3字母：各项的相同字母x所以，公因式是3x指数：相同字母的最低次幂13x2-6x=3x（x-2）想一想另一个因式x-2是如何得到的？ 提公因式法的一般步骤：1、确定应提取的公因式；2、用公因式去除这个多项式，所得的商作为另一个因式；3、把多项式写成两个或几个因式的积的形式。3x2-6x=3x（x-2） 8a3b2－12ab3c的公因式是什么？最大公约数相同字母最低次幂公因式4ab2一看系数二看字母三看指数步骤议一议 问:多项式中的公因式是如何确定的？多项式各项系数的最大公约数。（当系数是整数时）定系数：多项式各项中都含有的相同的字母。相同字母的指数取各项中字母的最低次幂。定字母：定指数： 注意：各项系数都是整数时，因式的系数应取各项系数的；字母取各项的的字母，而且各字母的指数取的.说出下列多项式各项的公因式：(1)ma+mb；(2)4kx－8ky；(3)5y3+20y2；m4k5y2最大公约数相同次数最低 练一练找出下列各多项式中的公因式：（1）8x+64（2）2ab2+4abc（3）m2n3-3n2m3(4)、a2b-2ab2+ab8m2n22ab提示：公因式的系数，字母，字母的指数ab 例:找2x2+6x的公因式。定系数2定字母x定指数23所以，公因式是2x2 例1把8a3b2+12ab3c分解因式.分析：找公因式1、系数的最大公约数42、找相同字母aｂ3、相同字母的最低指数a1b2公因式为：4ab2四、方法运用解:8a3b2+12ab3c=4ab2•2a2+4ab2•3bc=4ab2(2a2+3bc) 例2把9x2–6xy+3xz分解因式.=3x·3x-3x·2y+3x·z解：=3x(3x-2y+z)9x2–6xy+3xz用提公因式法分解因式的步骤：第一步.找出公因式；第二步.提取公因式；第三步.将多项式化成两个因式乘积的形式。 小冬解的有误吗？把8a3b2–12ab3c+ab分解因式.解：8a3b2–12ab3c+ab=ab·8a2b-ab·12b2c+ab·1=ab(8a2b-12b2c)当多项式的某一项和公因式相同时，提公因式后剩余的项是1。错误例3 ⑴提取公因式后，另一个因式不能再含有公因式；⑵另一个因式的项数与原多项式的项数一致。注意8a3b2–12ab3c+ab=ab(8a2b-12b2c+1) 例4：–24x3–12x2+28x解：原式==当多项式第一项系数是负数，通常先提出“”号，使括号内第一项系数变为正数，注意括号内各项都要变号。 把下列多项式分解因式：（1）12x2y+18xy2；（2）-x2+xy-xz；（3）2x3+6x2+2x现有甲、乙、丙三位同学各做一题，他们的解法如下：甲同学：解:12x2y+18xy2=3xy(4x+6y)乙同学：解:-x2+xy-xz=-x(x+y-z)丙同学：解:2x3+6x2+2x=2x(x2+3x)你认为他们的解法正确吗？试说明理由。乙同学：解:-x2+xy-xz=-x(x-y+z)丙同学：解:2x3+6x2+2x=2x(x2+3x+1) 练习:分解因式–a²+ab-ac-2x³+4x²+2x=−a(a−b+c)=−2x(x²−2x−1) 把下列各式分解因式:24x3y-18x2y7ma+14ma2(3)-16x4+32x3-56x2(4)-7ab-14abx+49aby随堂练习 2、确定公因式的方法：一看系数　二看字母　三看指数小结3、提公因式法分解因式步骤(分三步)：第一步，找出公因式；第二步，提公因式；第三步，将多项式化成两个因式乘积的形式。1、什么叫因式分解？4、用提公因式法分解因式应注意的问题：（1）公因式要提尽；（2）小心漏掉（3）多项式的首项取正号 例4：把2a(b+c)-5(b+c)分解因式(b+c)(b+c)解：2a(b+c)－5(b+c)=(b+c)(2a-5)注意：公因式可以是数字，字母，也可以是单项式，还可以是多项式。 例5把2a(b+c)-3(b+c)分解因式.分析:(b+c)是这个式子的公因式,可以直接提出.解:2a(b+c)–3(b+c)=(b+c)(2a-3). 练习三、把下列各式分解因式：（1）x(a+b)+y(a+b)（2）3a(x-y)-(x-y)（3）6(p+q)2-12(p+q)解：（1）原式=(a+b)（x+y）（2）原式=(x-y)（3a-1）（3）原式=6(p+q)(p+q-2) 解：6（m－n）3－12（n－m）2=6（m－n）3－12［－（m－n）］2=6（m－n）3－12（m－n）2=6（m－n）2（m－n－2）.6（m－n）3－12（n－m）2例6 (1)2-a=___(a-2)(2)y-x=___(x-y)(3)b+a=___(a+b)(4)-m-n=___(m+n)(5)(b-a)2=(a-b)2(6)-s2+t2=(s2-t2)(7)(x-y)3=(y-x)3--+-+--这些在分解因式时，都可当做公因式，但要注意符号.填空：（填入“+”或“-”） 例、用提取公因式法分解因式5a(x-y)-10b(y-x),提取的公因式应该是什么？并将其因式分解.公因式为5(x-y)解：原式=5a(x-y)+10b(x-y)=5(x-y)(a+2b) 解：ab2+a2b-a-b=ab(b+a)-(a+b)=(a+b)(ab-1)=5×(4-1)=15练习.已知a+b=5，ab=4，求ab2+a2b-a-b的值. 拓展与提高试一试能被2005整除吗计算 把一个多项式化为几个整式的乘积形式，这就是因式分解。公因式就是系数取各项式的最大公因数，字母取共有的字母指数取最低次幂（三看）因式分解的方法：提公因式法课堂小结 用提公因式法分解因式应注意的问题：（1）公因式要提尽；（2）小心漏掉“1“；（3）多项式的首项取正号；（4）公因式是多项式时，要注意符号问题。.（5）分接的结果一定是几个整式的乘积的形式.（6）要分解到不能分解为止.分解因式与整式乘法是互逆过程 D（2）分解-4x3+8x2+16x的结果是（）（A）-x（4x2-8x+16）（B）x（-4x2+8x-16）（C）4（-x3+2x2-4x）（D）-4x（x2-2x-4）（1）多项式6ab2+18a2b2-12a3b2c的公因式（）（A）6ab2c（B）ab2（C）6ab2（D）6a3b2CC1.选择课后练习 试一试拓展应用 (1)2101+299能被5整除吗,为什么转化为有一因式为5的倍数(2)224-1能被63和65整除吗? (3)若多项式-6ab+18abx+24aby的一个因式是-6ab，那么另一个因式是（）（A）-1-3x+4y（B）1+3x-4y（C）-1-3x-4y（D）1-3x-4yD选择题(4)若多项式(a+b)x2+(a+b)x要分解因式,则要提的公因式是.(a+b)x 若a=101,b=99,求a2-b2的值.若x=-3,求20x2-60x的值.1993-199能被200整除吗?还能被哪些整数整除? ①ax+ay+a②3mx-6nx2③4a2b+10ab2④x4y3+x3y3⑤12x2yz-9x3y2找公因式的方法：①系数取各系数的最大公约数；②字母取各项的相同字母，而且各字母的指数取次数最低的。指出下列各多项式中各项的公因式,并试着分解因式。a公因式3x2abx3y33x2y课堂练习一 例2:分解因式8a³b-12ab³c+ab解:原式=ab·8a²-ab·12b²c+ab·1=ab(8a²-12b²c+1)判断下列分解因式正确吗2x²+3x³+x=x(2x+3x²)3a²c-6a³c=3a²(c-2ac)X(2X+3X²+1)3a²c(1-2a)注意:提取公因式后：(1)另一个因式不能再含有公因式(2)另一个因式的项数与原多项式的项数一致我做得对吗？不要漏掉1如果多项式的某一项正好是公因式，要注意该项在提取了公因式后，应该用“1”顶替它原来的位置，切不可把“1”漏掉。 輕鬆又健康的十巧手 第一巧：虎口平击36次说明：打击大肠经／合谷穴。主治：预防及治疗颜面部位的疾病。如视力模糊、鼻炎、口齿疼痛、头痛及预防感冒。 第二巧：手掌侧击36次。说明：打击小肠经／后溪穴。主治：头项强痛、放松颈项肌肉群及预防骨刺、骨头退化。 第三巧：手腕互击36次。说明：打击心经及心包络经／大陵穴。主治：预防及治疗心脏病、胸痛、胸闷、纾解紧张的情绪。 第四巧：虎口交叉互击36次。说明：穴位是八邪穴。主治：预防及治疗末梢循环，如手麻、脚麻等末梢循环疾病。 第五巧：十指交叉互击36次说明：穴位是八邪穴。主治：预防及治疗末梢循环，如手麻、脚麻等末梢循环疾病。 第六巧：左拳击右掌心36次。说明：经络是心经和心包络经／劳合穴。主治：消除疲劳及提神的作用。 第七巧：右拳击左掌心36次。说明：经络是心经和心包络经／劳合穴。主治：消除疲劳及提神的作用。 第八巧：手背互相拍击36次。说明：打击到的是三集经／阳池穴。主治：调整内脏机能、预防及治疗糖尿病。 第九巧：搓揉双耳36次。说明：耳垂的穴位很多。主治：眼点、颜面部及脑部等部位的循环。 第十巧：手掌心互相摩擦6下至微热，轻盖双眼，眼球向左右转动6圈说明：运用气功原理，调整眼睛的经气。主治：预防近视、老花及视力模糊。 祝大家身体健康'