最新时域有限差分方法林志立课件PPT.ppt 45页

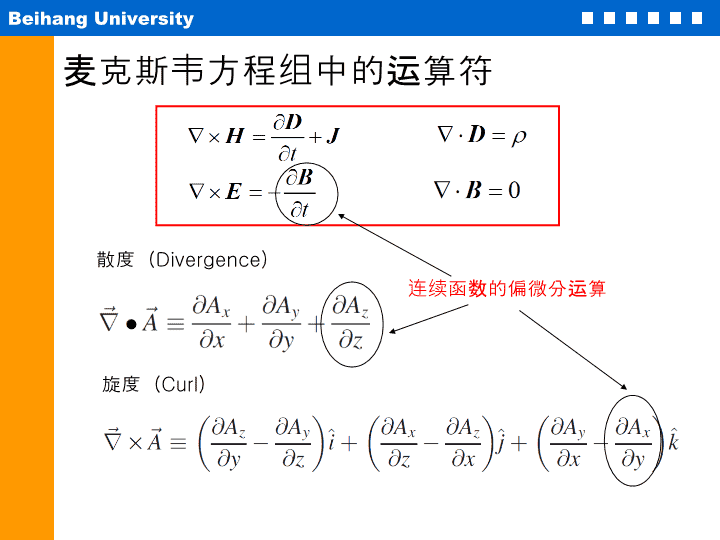
'时域有限差分方法林志立 电磁学基本方程麦克斯韦方程组(MaxwellEquations)JamesClerkMaxwell(1831–1879)(法拉第感应定律)(安培环路定律)(高斯定律－电场)(高斯定律－磁场)物质本构关系(ConstitutiveRelations)（欧姆定律）（电极化）（磁化）一切电磁场和电磁波问题均可由以上方程，以及各类具体的边界条件所决定！ 麦克斯韦方程组中的运算符散度（Divergence)旋度（Curl)连续函数的偏微分运算 FDTD空间偏微分的近似以Hz为例：类似地，可实现各电磁场分量的空间偏微分计算。 FDTD时间偏微分的近似以Hz为例：t=(n+1/2)Δtt=nΔtt=(n-1/2)Δt时间上的推移(1)电场在时间上取整数倍的Δt;t=n*Δt;(2)磁场在时间上取(整数＋1/2)倍的Δt;t=(n+1/2)*Δt; 麦克斯韦方程的离散化近似以Hz为例：上式即为Hz的更新方程，由前一时刻的磁场和前半时刻的临近空间格点的电场即可求出最新时刻的磁场。 麦克斯韦方程的离散化近似采取类似的步骤，可以推导出其它场量的更新表达式：例如，对于Ez： FDTD的离散参数的选择★元胞尺寸：边长小于最短波长的1/10,以减小数值色散。数值色散方程：理想色散方程：要求：例如，取例如，取 FDTD的离散参数的稳定性条件★时间步长：Courant稳定性条件对于非色散介质，时间步长不能大于以下表达式：（vonNeumannmethod）为了保持稳定性，该方程的所有解的模必须小于1。Ｚ域数值色散方程： 介质电磁参量的设定不同的元胞的电磁参量应设置为所在空间所代表的介质的介电常数和磁导率。长方体，物质I长方体，物质II球体，物质III空气场量与介质参数要对应 色散介质的FDTD模拟以Lorentz介质为例：更新方程：近似，求系数Z-变换时域：频域： 色散介质的FDTD模拟模拟Lorentz色散介质的不同方法：MSEapproach: FDTD编程流程主循环初始化输出结果 编程举例1：一维FDTD问题x基本旋度方程：X向电导率X向磁电导率X向电流X向磁流 编程举例1：一维FDTD问题Matlab程序代码：%Defineinitialconstantseps_0=8.854187817e-12;%permittivityoffreespacemu_0=4*pi*1e-7;%permeabilityoffreespacec=1/sqrt(mu_0*eps_0);%speedoflight%Defineproblemgeometryandparametersdomain_size=1;%1Dproblemspacelengthinmetersdx=1e-3;%cellsizeinmetersdt=3e-12;%durationoftimestepinsecondsnumber_of_time_steps=2000;%numberofiterationsnx=round(domain_size/dx);%numberofcellsin1Dproblemspacesource_position=0.5;%positionofthecurrentsourceJz1.定义物理常量2.定义问题的参量和结构尺寸 %InitializefieldandmaterialarraysCeze=zeros(nx+1,1);Cezhy=zeros(nx+1,1);Cezj=zeros(nx+1,1);Ez=zeros(nx+1,1);Jz=zeros(nx+1,1);eps_r_z=ones(nx+1,1);%freespacesigma_e_z=zeros(nx+1,1);%freespaceChyh=zeros(nx,1);Chyez=zeros(nx,1);Chym=zeros(nx,1);Hy=zeros(nx,1);My=zeros(nx,1);mu_r_y=ones(nx,1);%freespacesigma_m_y=zeros(nx,1);%freespace编程举例1：一维FDTD问题（续）3.初始化场量和介质参量阵列电场电流部分磁场磁流部分 %CalculateFDTDupdatingcoefficientsCeze=(2*eps_r_z*eps_0-dt*sigma_e_z)..../(2*eps_r_z*eps_0+dt*sigma_e_z);Cezhy=(2*dt/dx)..../(2*eps_r_z*eps_0+dt*sigma_e_z);Cezj=(-2*dt)..../(2*eps_r_z*eps_0+dt*sigma_e_z);Chyh=(2*mu_r_y*mu_0-dt*sigma_m_y)..../(2*mu_r_y*mu_0+dt*sigma_m_y);Chyez=(2*dt/dx)..../(2*mu_r_y*mu_0+dt*sigma_m_y);Chym=(-2*dt)..../(2*mu_r_y*mu_0+dt*sigma_m_y);编程举例1：一维FDTD问题（续）4.计算更新方程系数电场部分磁场部分 %DefinetheGaussiansourcewaveformtime=dt*[0:number_of_time_steps-1].";Jz_waveform=exp(-((time-2e-10)/5e-11).^2);source_position_index=round(nx*source_position/domain_size)+1;%Subroutinetoinitializeplottinginitialize_plotting_parameters;编程举例1：一维FDTD问题（续）5.定义场源源波形为高斯型6.作图初始化Ez_positions=[0:nx]*dx;Hy_positions=([0:nx-1]+0.5)*dx;v=[0-0.1-0.1;0-0.10.1;00.10.1;00.1-0.1;...1-0.1-0.1;1-0.10.1;10.10.1;10.1-0.1];f=[1234;5678];axis([01-0.20.2-0.20.2]);lez=line(Ez_positions,Ez*0,Ez,"Color","b","LineWidth",1.5);lhy=line(Hy_positions,377*Hy,Hy*0,"Color","r",..."LineWidth",1.5,"linestyle","-.");set(gca,"fontsize",12,"FontWeight","bold");axissquare;legend("E_{z}","H_{y}times377","Location","NorthEast");xlabel("x[m]");ylabel("[A/m]");zlabel("[V/m]");gridon;p=patch("vertices",v,"faces",f,"facecolor","g","facealpha",0.2);text(0,1,1.1,"PEC","horizontalalignment","center","fontweight","bold");text(1,1,1.1,"PEC","horizontalalignment","center","fontweight","bold"); %FDTDloopfortime_step=1:number_of_time_steps%UpdateJzforthecurrenttimestepJz(source_position_index)=Jz_waveform(time_step);%UpdatemagneticfieldHy(1:nx)=Chyh(1:nx).*Hy(1:nx)...+Chyez(1:nx).*(Ez(2:nx+1)-Ez(1:nx))...+Chym(1:nx).*My(1:nx);%UpdateelectricfieldEz(2:nx)=Ceze(2:nx).*Ez(2:nx)...+Cezhy(2:nx).*(Hy(2:nx)-Hy(1:nx-1))...+Cezj(2:nx).*Jz(2:nx);Ez(1)=0;%ApplyPECboundaryconditionatx=0mEz(nx+1)=0;%ApplyPECboundaryconditionatx=1m%Subroutinetoplotthecurrentstateofthefieldsplot_fields;end编程举例1：一维FDTD问题（续）7.主循环程序引入电流源更新磁场更新电场设置完美电导层跟新图面 %subroutineusedtoplot1Dtransientfieldsdelete(lez);delete(lhy);lez=line(Ez_positions,Ez*0,Ez,"Color","b","LineWidth",1.5);lhy=line(Hy_positions,377*Hy,Hy*0,"Color","r",..."LineWidth",1.5,"linestyle","-.");ts=num2str(time_step);ti=num2str(dt*time_step*1e9);title(["timestep="ts",time="ti"ns"]);drawnow;编程举例1：一维FDTD问题（续）7.更新画面运行程序:fdtd_1d_code.m 开放模拟空间的模拟完美匹配层（PerfectlyMatchedLayer)的概念吸波材料（损耗介质） 完美匹配层（PerfectlyMatchedLayer)材料的特点 形成PML必须符合的两个条件:从计算空间到PML层的阻抗必须一直匹配:2.某方向的电磁参量必须是另一个方向电磁参量的倒数完美匹配层（PerfectlyMatchedLayer)材料的特点 下面的材料就符合这些条件：阻抗始终是相等的：电导率s随着PML的层数号（x)而逐渐增加,提高吸收外行电磁波的能力。完美匹配层（PerfectlyMatchedLayer)材料的特点 完美匹配层PML的验证实例中心有一光源，四周被PML环绕可以看到外形电磁波被完美吸收，没有反射。运行程序:fd2d_pml_code.m 功率放大电路 甲类功放乙类功放甲乙类功放 乙类双电源互补对称功放电路 乙类双电源互补对称功放电路 分析计算正半周T1管工作情况 双管互补对称工作情况 输出功率：最大功率： 两管管耗： 直流电源供给的功率：电源供给的最大功率： 一般情况下的效率：当VOM≈VCC时的效率： 乙类互补对称电路存在交越失真 甲乙类互补对称功放电路 甲乙类双电源互补对称电路 甲乙类单电源互补对称电路 带自举的单电源互补对称电路'