二次函数y_a2+c_的图象和性质课件PPT 16页

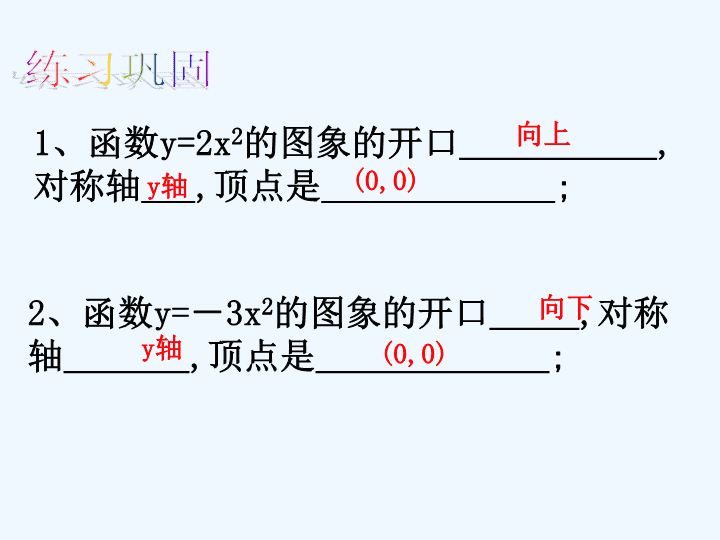
'26.1二次函数(3)二次函数y=ax2+k的图象和性质 y＝ax2a>0a<0图象二次函数y=ax2的图象与性质开口方向开口大小对称轴顶点开口向上开口向下a的绝对值越大，开口越小y轴顶点是原点（0，0）x0yxy0复习a的正负决定抛物线的什么？a的大小决定什么的？ 1、函数y=2x2的图象的开口,对称轴,顶点是;2、函数y=－3x2的图象的开口,对称轴,顶点是;向上向下y轴y轴(0,0)(0,0)练习巩固 例2.在同一直角坐标系中,画出二次函数y=x2+1和y=x2－1的图像解:先列表x…-3-2-10123…y=x2+1y=x2-1…105212510……830-1038…然后描点,连线,得到y=x2＋1,y=x2－1的图像.12345x12345678910yo-1-2-3-4-5y=x2+1y=x2－1 (1)抛物线y=x2+1,y=x2－1的开口方向、对称轴、顶点各是什么?讨论抛物线y=x2+1:开口向上,顶点为(0,1).对称轴是y轴,抛物线y=x2－1:开口向上,顶点为(0,－1).对称轴是y轴,12345x12345678910yo-1-2-3-4-5y=x2+1y=x2－1●● (2)抛物线y=x2+1,y=x2－1与抛物线y=x2的异同点:12345x12345678910yo-1-2-3-4-5y=x2+1抛物线y=x2抛物线y=x2－1向上平移1个单位抛物线y=x2向下平移1个单位y=x2－1y=x2抛物线y=x2+1相同点：①形状大小相同②开口方向相同③对称轴相同不同点：顶点的位置不同，抛物线的位置也不同．●●● 总结抛物线y=ax2与y=ax2±k之间的关系是：形状大小相同，开口方向相同，对称轴相同，而顶点位置和抛物线的位置不同．抛物线之间的平移规律：抛物线y=ax2抛物线y=ax2－k向上平移c个单位抛物线y=ax2向下平移c个单位抛物线y=ax2+k 归纳一般地,抛物线y=ax2+k有如下特点:(1)对称轴是y轴;(2)顶点是(0,c).12345x12345678910yo-1-2-3-4-5(3)抛物线的开口方向由a的符号决定 把抛物线y=２x2向上平移5个单位,会得到那条抛物线?向下平移3.4个单位呢?例题１思考:抛物线y=2x2+5的开口方向、对称轴、顶点各是什么?(1)得到抛物线y=２x2+5(2)得到抛物线y=２x2－３.4 例题２抛物线y=－　x2向下平移５个单位后，所得抛物线为，再向上平移７个单位后，所得抛物线为.12y=－　x2－５12y=－　x2＋２12 抛物线y=ax2＋k与y=－５x2的形状大小，开口方向都相同，且其顶点坐标是（０，３），则其表达式为，它是由抛物线y=－５x2向平移个单位得到的．例题３y=－５x2＋３上３ 抛物线y=ax2＋k与y=３x2的形状相同，且其顶点坐标是（０，１），则其表达式为，例题４y=３x2＋１或y=－３x2＋１ １、在直角坐标系中，二次函数y=3x2+2的图象大致是下图中的()ABCD练习Ax0y0xyx0y0xy 2、函数y=3x2+5与y=3x2的图象的不同之处是()A.对称轴B.开口方向C.顶点和抛物线的位置D.形状C 3、按下列要求求出抛物线的解析式：（1）　抛物线y=ax2＋k形状与y=-2x2+3的图象形状相同，但开口方向不同，顶点坐标是（0，1）,求抛物线的解析式。（2）抛物线y=ax2＋k对称轴是y轴，顶点（0，-3），且经过（1，2），求抛物线的解析式. 小结抛物线y=ax2与y=ax2±k之间的关系是：形状大小相同，开口方向相同，对称轴相同，而顶点位置和抛物线的位置不同．抛物线之间的平移规律：抛物线y=ax2抛物线y=ax2－k向上平移c个单位抛物线y=ax2向下平移c个单位抛物线y=ax2+k'