最新大一高数教案ppt课件PPT课件 58页

'大一高数教案ppt课件 一、问题的提出1.自由落体运动的瞬时速度问题如图,取极限得 播放2.导函数(瞬时变化率)是函数平均变化率的逼近函数. ★2.右导数:单侧导数1.左导数:★ ★★ 三、由定义求导数步骤:例1解 例2解 例3解更一般地例如, 例4解 例5解 例6解 四、导数的几何意义与物理意义1.几何意义切线方程为法线方程为 例7解由导数的几何意义,得切线斜率为所求切线方程为法线方程为 2.物理意义非均匀变化量的瞬时变化率.变速直线运动:路程对时间的导数为物体的瞬时速度.交流电路:电量对时间的导数为电流强度.非均匀的物体:质量对长度(面积,体积)的导数为物体的线(面,体)密度. 五、可导与连续的关系定理凡可导函数都是连续函数.证 连续函数不存在导数举例0例如,注意:该定理的逆定理不成立.★ 01例如, 例如,011/π－1/π 例8解 六、小结1.导数的实质:增量比的极限;3.导数的几何意义:切线的斜率;4.函数可导一定连续，但连续不一定可导;5.求导数最基本的方法:由定义求导数.6.判断可导性不连续,一定不可导.连续直接用定义;看左右导数是否存在且相等. 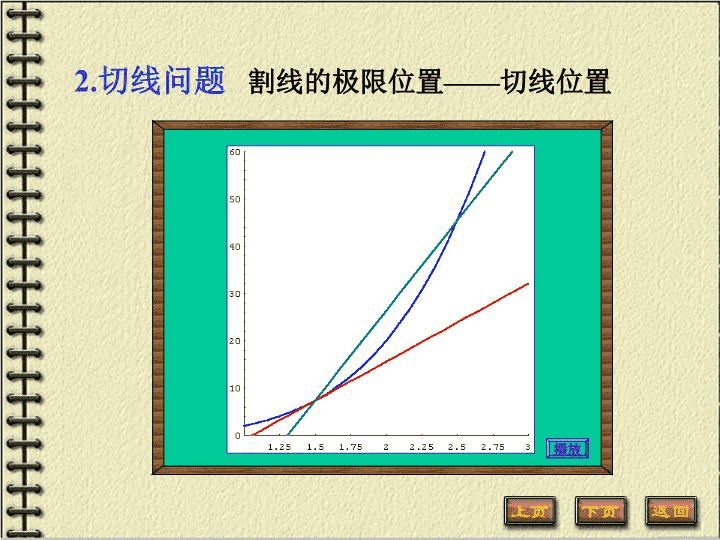思考题 思考题解答 练习题答案 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.切线问题割线的极限位置——切线位置 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 2.导函数(瞬时变化率)是函数平均变化率的逼近函数. 结束语谢谢大家聆听！！！58'