数学分析课件PPT之第二章数列极限 105页

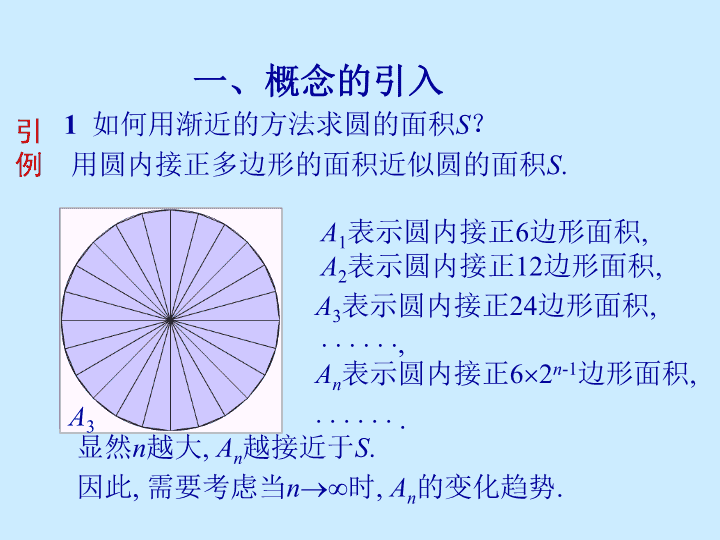
'第二章数列极限§2.1数列极限的概念§2.2收敛数列的性质§2.3数列极限存在的条件 §2.1数列极限的概念一、概念的引入二、数列的定义三、数列的极限四、应用数列极限的定义证明数列极限的方法 一、概念的引入引例1如何用渐近的方法求圆的面积S？用圆内接正多边形的面积近似圆的面积S.A1A2A3A1表示圆内接正6边形面积,A2表示圆内接正12边形面积,A3表示圆内接正24边形面积,An表示圆内接正62n-1边形面积,,.显然n越大,An越接近于S.因此,需要考虑当n时,An的变化趋势. 2、截丈问题：“一尺之棰，日截其半，万世不竭” 二、数列的定义例如 注意：1.数列对应着数轴上一个点列.可看作一动点在数轴上依次取2.数列是整标函数 数列极限来自实践，它有丰富的实际背景.我们的祖先很早就对数列进行了研究，早在战国时期就有了极限的概念例1战国时代哲学家庄周所著的《庄子.天下篇》引用过一句话：“一尺之棰，日取其半，万世不竭。”也就是说一根一尺长的木棒，每天截去一半，这样的过程可以一直无限制的进行下去。将每天截后的木棒排成一列,如图所示,三、数列的极限 （c11(k)）其长度组成的数列为,024681000.20.40.60.81随着n无限的增加,木棒的长度无限的趋近于零。 例如当n无限增大时,如果数列{xn}的一般项xn无限接近于常数a,则常数a称为数列{xn}的极限,或称数列{xn}收敛a,记为数列极限的通俗定义 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 三、数列的极限 问题:当无限增大时,是否无限接近于某一确定的数值?如果是,如何确定?问题:“无限接近”意味着什么?如何用数学语言刻划它.通过上面演示实验的观察: 当n无限增大时,xn无限接近于a.当n无限增大时,|xn-a|无限接近于0.当n无限增大时,|xn-a|可以任意小,要多小就能有多小.当n增大到一定程度以后,|xn-a|能小于事先给定的任意小的正数.分析因此,如果n增大到一定程度以后,|xn-a|能小于事先给定的任意小的正数,则当n无限增大时,xn无限接近于常数a.当n无限增大时,如果数列{xn}的一般项xn无限接近于常数a,则数列{xn}收敛a.下页 数列极限的精确定义设{xn}为一数列如果存在常数a对于任意给定的正数e总存在正整数N使得当n>N时不等式|xna|N目的：NO,有些点在条形域外面！●●●●●●●●●●●●●●●●●●数列极限的演示 N数列极限的演示e越来越小，N越来越大！ 数列极限的定义未给出求极限的方法.例1证所以,注意： 分析:例1证明下页0,NN当nN时有|xna|. 利用定义验证数列极限，有时遇到的不等式|xn－a|＜ε不易考虑，往往采用把|xn－a|放大的方法。若能放大到较简单的式子，就较容易从一个比较简单的不等式去寻找项数指标N放大的原则：①放大后的式子较简单②放大后的式子以0为极限例2证明证明 则当n＞N时，有 例3.证明分析，要使（为简化，限定n只要证.当n>N时有由定义适当予先限定n＞n。是允许的！但最后取N时要保证n＞n。 .例4.证明（K为正实数）证：由于所以对任意ε＞0，取N=,当n＞N时,便有 例5证所以,说明:常数列的极限等于同一常数.小结:用定义证数列极限存在时,关键是任意给定寻找N,但不必要求最小的N. 例6证 例7证 由上面数列极限的证明可总结出数列极限证明的步骤：2适当放大，通常放大成的形式，求出需要的1化简3解总结用定义求极限或证明极限的关键是适当放大不等式，关键的追求有两点，一是把隐性表达式变成显性表达式，在重锁迷雾中看清庐山真面目，二是抓住主要矛盾，舍去次要矛盾；要取舍合理，不能放大得过份。 四收敛的否定:＞数列发散＞＞＞ 五数列极限的记註:1满足条件“”的数列:。2改变或去掉数列的有限项,不影响数列的收敛性和极限.重排不改变数列敛散性: 3数列极限的等价定义:对对任正整数 六无穷小数列:定义极限为0的数列称为无穷小量（无穷小量是指一个极限概念，趋向常数0）命题1.的极限为n<=>是无穷小量.变量有极限的充要条件为它可分解为加一个无穷小量。命题2无穷小量加绝对值仍为无穷小量。命题3无穷小量与有界变量的积仍为无穷小量。命题4 小结(1),数列极限的定义;(2),数列极限的几何意义;(3),应用数列极限的定义证明数列极限的方法. §2.2收敛数列的性质1、唯一性2、有界性3、保号性4、保不等式性5、四则运算6、迫敛性7、子数列的收敛性 1、唯一性定理2.2每个收敛的数列只有一个极限.证由定义,故收敛数列极限唯一. 2、有界性例如,有界无界 定理2.3收敛的数列必定有界.证由定义,注意：有界性是数列收敛的必要条件.推论无界数列必定发散. 例1证由定义,区间长度为1.不可能同时位于长度为1的区间内. 3保序性 从而 定理2.6(收敛数列的保号性)如果数列{xn}收敛于a,且a0(或a0)那么存在正整数N当nN时有xn0(或xn0)4保号性 推论如果数列{xn}从某项起有xn0(或xn0)且数列{xn}收敛于a那么a0(或a0)这说明若数列收敛且极限不为零，则当n充分大时，与0的距离不能任意小.这一事实在后面讨论极限的四则运算时会用到. 证5迫敛性(双逼原理) 上两式同时成立,上述数列极限存在的准则可以推广到函数的极限 例2解由夹逼定理得 6绝对值收敛性:(注意反之不成立).推论设数列{}和{}收敛,则 7数列极限的四则运算法则定理2.8设有数列{xn}和{yn}如果那么 例5求例4求解：分a=1，|a|<1，|a|>1三种情况解：（分子有理化）例3求 8、子数列的收敛性注意：例如， 定理7收敛数列的任一子数列也收敛．且极限相同．证证毕． 例6对于数列xn证此时有 此时有总之：恒有 Th(数列收敛充要条件){}收敛{Th(数列收敛充要条件){}收敛子列{}和{收敛于同一极限.}的任何子列收敛于同一极限.}Th(数列收敛充要条件){}收敛子列{}、{}都收敛.和{ 思考题证明要使只要使从而由得取当时，必有成立 思考题解答~（等价）证明中所采用的实际上就是不等式即证明中没有采用“适当放大”的值 从而时，仅有成立，但不是的充分条件．反而缩小为 小结(1),唯一性;(2),有界性;(3),保号性;(4),四则运算法则;(5),不等式性;(6),收敛数列与其子列的关系. §2.3数列极限存在的条件一数列收敛的一个充分条件——单调有界原理二数列收敛的充要条件——Cauchy收敛准则三关于极限四数列单调有界证法欣赏 一单调有界原理定义称为单调上升的，若称为单调下降的，若单调增加和单调减少数列统称为单调数列提问:收敛的数列是否一定有界？有界的数列是否一定收敛？ M定理1(单调有界定理)单调有界数列必有极限定理1的几何解释x1x5x4x3x2xnA以单调增加数列为例数列的点只可能向右一个方向移动或者无限向右移动或者无限趋近于某一定点A而对有界数列只可能后者情况发生数列极限存在的条件 数列极限存在的条件定理1(单调有界定理)单调有界数列必有极限证明 例1设证明数列{}收敛.例2例3(n重根号),···证明数列单调有界,并求极限.求(计算的逐次逼近法,亦即迭代法).解由均值不等式,有有下界; 注意到对有有↘···,例41）证明序列的极限存在；2）求极限 解1）因时有所以即有 故序列下降。因此序列极限存在，记极限值为c。于是这表明序列有下界。又或 2）因所以又即得 二数列收敛的充要条件——Cauchy收敛准则1Cauchy列：如果数列具有以下特性：＞＞＜则称数列是一个基本数列.（Cauchy列）2Cauchy收敛准则：定理数列收敛的充要条件是：是一个基本数列.数列收敛或 数列极限存在的条件定理的几何解释柯西准则说明收敛数列各项的值越到后边,彼此越是接近,以至充分后面的任何两项之差的绝对值可小于预先给定的任意小正数.或形象地说,收敛数列的各项越到后面越是挤在一起.x1x2x3x4x5 例5证明:任一无限十进小数的不足近似值所组成的数列收敛.其中是中的数.证令有 …… 三.关于极限（证明留在下段进行.）例8例9例10 四数列证法一单调有界证法欣赏:Cauchy(1789—1857)最先给出这一极限，Riemann（1826—1866）最先给出以下证法一.设用二项式展开，得 注意到且比多一项即↗. 有界.综上,数列{}单调有界.评註:该证法朴素而稳健,不失大师风度.证法二(利用Bernoulli不等式)注意到Bernoulli不等式为正整数),有 小结(1),单调有界定理;(2),单调有界定理的几何意义;(3),柯西收敛准则;(4),柯西收敛准则的几何解释.'