数学分析课件PPT之十一章反常积分 61页

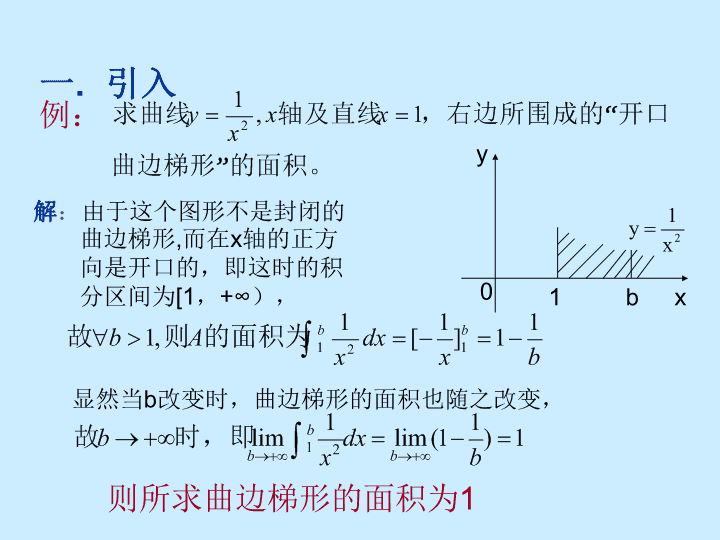
'第十一章反常积分11.1反常积分概念11.2无穷积分的收敛性质与判别11.3瑕积分的性质与收敛判别 11.1反常积分概念一、引例二、两类反常积分的定义 一.引入例：0xy1b解：由于这个图形不是封闭的曲边梯形,而在x轴的正方向是开口的，即这时的积分区间为[1，+∞），显然当b改变时，曲边梯形的面积也随之改变，则所求曲边梯形的面积为1 二、两类反常积分的定义.定义1:设函数f(x)在区间[a,+)上连续,取b>a,如果极限存在,则称此极限为函数f(x)在无穷区间[a,+)上的无穷限反常积分,记作(1) 这时也称无穷积分收敛;若上述极限不存在,就称无穷积分发散,这时记号不再表示数值了。例如：oyxb1 类似地,设函数f(x)在区间(,b]上连续,取aò¥+-ppdttept且是常数计算无穷积分例 证:当p=1时当p1时).0(:3>ò¥+axdxap证明无穷积分例 ò¥+apxdx所以无穷积分 练习1.确定下列无穷积分是否收敛，若收敛算出它的值.解： 练习2：计算无穷积分解(1): 练习4：求下列无穷积分： 定义2:设函数f(x)在区间(a,b]上连续,而在点a的右邻域内无界,取>0.如果极限存在,则称此极限为无界函数f(x)在(a,b]上的反常积分.(4)这时也称反常积分收敛.如果上述极限不存在,就称反常积分发散. 类似地,设函数f(x)在区间[a,b)上连续,而在点b的左邻域内无界,取>0.存在,则定义如果极限(5)否则,就称反常积分发散. 设函数f(x)在区间[a,b]上除点c(a-òaxadxa计算反常积分例 且由于.:5112ò-的收敛性讨论反常积分例xdx 当q<1时,收敛;当q1时,发散.证:当q=1时)(:6ò-baqaxdx证明反常积分例 当q1时,因此,当q<1时,反常积分收敛,其值为当q1时,广义积分发散. 例7计算反常积分解故原反常积分发散. 例8.解:被积函数f在(0,1]上连续,x=0是瑕点.由于. 瑕点解例9计算反常积分 注意反常积分与定积分不同，尤其是瑕积分，它与定积分采用同一种表达方式，但其含义却不同，遇到有限区间上的积分时，要仔细检查是否有瑕点。反常积分中，N-L公式，换元积分公式、分部积分公式仍然成立，不过代入上、下限时代入的是极限值。 如无穷限积分再如瑕积分 例10证明证 四.小结(1)无穷积分和瑕积分的定义;(2)无穷积分和瑕积分收敛与发散的定义;(3)无穷积分的计算：(i).求出函数f(x)的原函数F(x).(ii). 11.2无穷积分的收敛性质与判别一.无穷积分的性质二.无穷积分收敛的判别法 一.无穷积分的性质性质１性质２ 性质３注性质３说明绝对收敛的级数自身一定收敛．但自身收敛的级数不一定绝对收敛．我们称收敛而不绝对收敛的级数为条件收敛． 二.无穷积分收敛的判别法２，比较原则１，柯西准则 ２，比较原则推论 ３，柯西判别法推论 ４，狄利克雷判别法５，阿贝尔判别法 解：例1.讨论　　　　　　收敛性，根据比较原则 例2.讨论下列无穷积分的收敛性，解(1)：根据柯西判别法解(２)：根据柯西判别法 例3解根据比较原则，.1134的收敛性判别无穷积分ò¥++xdx.1134收敛无穷积分ò¥++xdx 例4解根据极限判别法，所给广义积分发散．例5解根据极限判别法，所给无穷积分发散．.arctan1的收敛性判别无穷积分dxxxò¥+ 证即收敛. 例解所以所给无穷积分收敛. 小结一.无穷积分的性质二.无穷积分收敛的判别法１.柯西准则２.比较原则３.柯西判别法４.狄利克雷判别法５.阿贝尔判别法 11.3瑕积分的性质与收敛判别瑕积分与无穷积分有平行的理论和结果. 一.瑕积分的性质性质１性质２ 性质３注性质３说明绝对收敛的级数自身一定收敛．但自身收敛的级数不一定绝对收敛．我们称收敛而不绝对收敛的级数为条件收敛． 二.无穷积分收敛的判别法１.柯西准则 ２，比较原则推论 ３.柯西判别法推论 例1例2 例3解由洛必达法则知根据柯西判别法极限形式,所给广义积分发散. 例4解根据比较判别法, 特点:1.积分区间为无穷; －函数的几个重要性质： 小结一.瑕积分的性质二.暇积分收敛的判别法１.柯西准则２.比较原则３.柯西判别法４.狄利克雷判别法５.阿贝尔判别法'