- 686.00 KB
- 2022-04-29 14:19:52 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'24.1.4圆周角
一.复习引入:1.圆心角的定义?.OBC答:顶点在圆心并且两条角边都与圆相交的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦、弦心距四组量之间关系的一个结论,这个结论是什么?
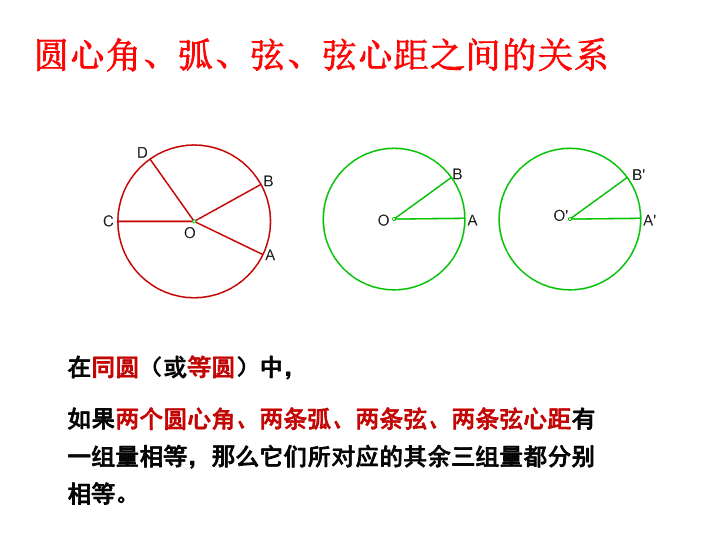
圆心角、弧、弦、弦心距之间的关系在同圆(或等圆)中,如果两个圆心角、两条弧、两条弦、两条弦心距有一组量相等,那么它们所对应的其余三组量都分别相等。
.OBCA圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
辩一辩图中的∠CDE是圆周角吗?CDECDECDECDE①角的顶点在圆上.②角的两边都与圆相交.特征:
类比圆心角探知圆周角在同圆或等圆中,同弧或等弧所对的圆心角相等.在同圆或等圆中,同弧或等弧所对的圆周角有什么关系?为了解决这个问题,我们先探究同弧所对的圆周角和圆心角之间有的关系.你会画同弧所对的圆周角和圆心角吗?
下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。(1)(2)(3)(4)(5)
如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.●OABC●OABC●OABC
圆周角和圆心角的关系1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.∵∠AOC是△ABO的外角,∴∠AOC=∠B+∠A.∵OA=OB,●OABC∴∠A=∠B.∴∠AOC=2∠B.即∠ABC=∠AOC.同弧所对的圆周角等于它所对的圆心角的一半.老师期望:你可要理解并掌握这个模型.
如果圆心不在圆周角的一边上,结果会怎样?2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否转化为问题1的情况?过点B作直径BD.由1可得:●O∴∠ABC=∠AOC.同弧所对的圆周角等于它所对的圆心角的一半.ABCD∠ABD=∠AOD,∠CBD=∠COD,圆周角和圆心角的关系●OABC
圆周角和圆心角的关系如果圆心不在圆周角的一边上,结果会怎样?3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?老师提示:能否也转化为问题1的情况?过点B作直径BD.由1可得:●O∴∠ABC=∠AOC.同弧所对的圆周角等于它所对的圆心角的一半.D∠ABD=∠AOD,∠CBD=∠COD,ABC●OABC
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:同弧所对的圆周角等于它所对的圆心角的一半.●OABC●OABC●OABC即∠ABC=∠AOC.
如图所示,∠ADB、∠ACB、∠AOB分别是什么角?它们有何共同点?∠ADB与∠ACB有什么关系?
·ABC1OC2C3圆周角定理在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.推论·ABCDEO
1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?ABCD12345678∠1=∠4∠5=∠8∠2=∠7∠3=∠6跟踪练习方法点拔:由同弧来找相等的圆周角
2已知⊙O中弦AB的长等于半径,求弦AB所对的圆心角和圆周角的度数。OAB圆心角为60度圆周角为30度或150度。
圆周角在足球场上,当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角有何特点?它们的大小有什么关系?.●OBACBACBACBACBACBACBACDEDE顶点在圆上,并且两边都与圆相交的角,叫做圆周角.
圆内接多边形:所有顶点都在同一圆上的多边形。结论:圆内接四边形对角互补·OBCDA思考圆内接四边形的对角有何数量关系?
在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等吗?为什么??思考在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等.因为,在同圆或等圆中,如果圆周角相等,那么它所对的圆心角也相等,因此它所对的弧也相等.·CBOAFGE((
例2如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D点,求BC、AD、BD的长.又在Rt△ABD中,AD2+BD2=AB2,·ABCDO解:∵AB是直径,∴∠ACB=∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD.例题106))8∴∠ACD=∠BCD
练习:如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.ABOCD40°
练习:1、圆周角的两个特征(1)(2)2、在同圆或等圆中,一条弧所对的圆周角等于它所对的圆心角的。3、如图,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角,若∠BCD=25°,则∠AOD=。顶点在圆上两边都与圆相交一半130°
4、如图,AB是⊙O的直径,=,∠A=30°,则∠BOD=。5、如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,∠ACB与∠BAC的大小有什么关系?为什么?60°
6、如图,A、B、C、D是⊙O上的四个点,且∠BCD=100°,求∠BOD(所对的圆心角)和∠BAD的大小。
小结:1、圆周角的定义;2、圆周角定理及证明;3、圆周角定理的运用。作业:基础训练P103---104'