MATLAB在电工电子中的应用举例（课件PPT） 75页

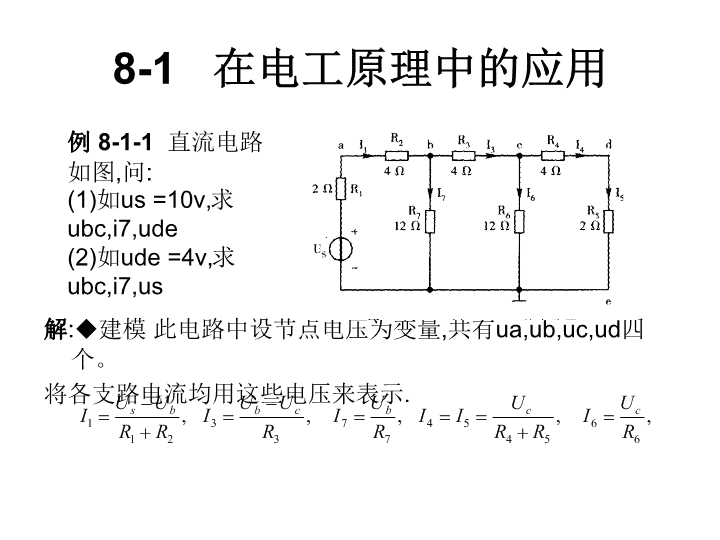
'第8章在电工电子中的应用 8-1在电工原理中的应用解:◆建模此电路中设节点电压为变量,共有ua,ub,uc,ud四个。将各支路电流均用这些电压来表示.例8-1-1直流电路如图,问:(1)如us=10v,求ubc,i7,ude(2)如ude=4v,求ubc,i7,us 方程的建立对b点和c点列出节点电流方程：I1=I3+I7，I3=I4+I6，将上述各值代入化简，得对问题（1）给出Us时，这两个方程中只有两个未知数Ub和Uc，可以写成矩阵方程 编程方法及运行结果读者可从方程（1），（2）中找到a11,a12,a21,a22及a13,a23的表达式，并用矩阵左除解出Ub和Uc。再由即可得到问题（1）的解。对问（2），可以推出类似的矩阵表达式，只是输入输出量不同，请读者自行推导,并与下面的程序exn811对照。由于同一系统的特征矩阵有许多相同的项,编程时可以利用这个特点来简化赋值过程◆运行程序exn811的结果为输入us=10时，ubc=2.2222,ude=0.7407,i7=0.3704输入ude=4时，ubc=12.0000,i7=2.0000,us=54.0000 程序exn811r1=2;r2=4;r3=4;r4=4;r5=2;r6=12;r7=12;%为元件赋值%将各系数矩阵赋值a11=1/(r1+r2)+1/r3+1/r7;a12=-1/r3;a13=1/(r1+r2);a21=1/r3;a22=-1/r3-1/(r4+r5)-1/r6;a23=0;us=input("us=");%输入解(1)的已知条件A1=[a11,a12;a21,a22]%列出系数矩阵A1u=A1[a13*us;0]%u=[ub;uc]ubc=u(1)-u(2),ude=u(2)*r5/(r4+r5),i=u(1)/r7%解(1)ude=input("ude="),%输入解(2)的已知条件A2=[A1,[a13;a23];0,r5/(r4+r5),0]%列出系数矩阵A2u=A2[0;0;ude],%u=[ub;uc;us]ubc=u(1)-u(2),i=u(1)/r7,us=(r1+r2)*(u(1)*a11+u(2)*a12)%解(2) 例8-1-2暂态分析如图所示电路，在t<0时开关K位于‘1’，电路已处于稳态，t=0时，开关K闭合到‘2’，求uC和ir2的响应，并画出它们的波形。解：◆建模这是一个分析暂态过程的问题。先要找到其初值和终值。 初值的分析在t=0时uc(0-)=-12v,ic(0-)=0，由于R2是电流源Is的唯一外部通路，故IR2(0-)=Is=3；当t=0+时，因为电容器端电压不可能突变,仍有uc(0+)=uc(0-)=-12v,电流源向两个电阻和一个电容的并联系统供电，两个电阻的电流应等于电容电压除以电阻，即而电容的充电电流为电流源电流减去电阻电流,故ic(0+)=is-ir2(0+)-ir3(0+)=3-(-1)-(-2)=6A 终值的分析再分析终值，达到稳态后，电容中将无电流，电流源的全部电流将在两个电阻之间分配，保证其端电压相同(也就是电容上的终电压)。结果应为ucf=12v,ir2f=1A.初值和终值之间的过渡波形u(t)按三要素计算。所谓三要素是指初值u0、终值uf和该段的充放电时常数T，表示式为：用MATLAB语句可写成：u=uf+(u0-uf)*exp(-(t-t0)/T).在求多段波形时，每段的初始时刻t0可能不同，需要予以注意。 程序exn812r1=3;us=18;is=3;r2=12;r3=6;C=1;%给出原始数据uc0=-12;ir20=uc0/r2;ir30=uc0/r3;%算出初值ic0=is-ir20-ir30;ir2f=is*r3/(r2+r3);%算出终值ir3f=is*r2/(r2+r3);ucf=ir2f*r2;icf=0;t=[[-2:0]-eps:0-eps,0:15];%注意在t=0附近设两个点uc(1:3)=-12;ir2(1:3)=3;%t<0时的值T=r2*r3/(r2+r3)*C;%求充电时常数uc(4:19)=ucf+(uc0-ucf)*exp(-t(4:19)/T);%ir2(4:19)=ir2f+(ir20-ir2f)*exp(-t(4:19)/T);%三要素法求输出 程序exn812运行结果%绘图语句subplot(2,1,1);h1=plot(t,uc),grid,set(h1,"linewidth",2)%加大线宽subplot(2,1,2),h2=plot(t,ir2);grid,set(h2,"linewidth",2)gtext("uc"),gtext("ir2")◆执行此程序的结果见图 例8-1-3交流电路右图所示电路,已知R=5欧姆,ωL=3欧姆,欧姆,Uc=10∠0°,求IR,I,I,和UL，Us.并画其相量图。解：建模：方程列写如下。令R与C并联后的阻抗为总阻抗为Z=Z1+Z23有得到， 程序exn813z1=3*j;z2=5;z3=5/j;uc=10;z23=z2*z3/(z2+z3);z=z1+z23;Ic=uc/z3,Ir=uc/z2,I=Ic+Ir,ul=I*z1,us=I*zdisp("IrIcIulus")disp("幅值"),disp(abs([Ir,Ic,I,ul,us]))disp("相角"),disp(angle([Ir,Ic,I,ul,us])*180/pi)%compass是MATLAB中绘制复数相量图的ha=compass([Ir,Ic,I,ul,us]);%ha是本图的图柄，如不需改变线宽，可省去左端set(ha,"linewidth",2);%把向量线条加粗至2毫米 程序exn813运行结果IrIcIulus幅值2.02.02.82848.48537.2111相角090.45.013556.3099画出的相量图见右。 例8-1-4交流电桥电路如图所示电路，已知Us=10+10cost，Is(t)=5+5cos2t，求U.解：◆建模这是一个含三个频率分量的稳态交流电路问题，可以按每个频率成份分别计算，再叠加起来。但是，更高明的办法是利用MATLAB的数组计算特性，把多个频率分量及相应的电压、电流、阻抗等都看作多元素的数组，每一元素对应于一种频率分量的值。因为他们服从同样的方程，所以程序就特别简洁,不过写程序时,与频率有关的量,如电压,电流,阻抗等之间的运算都要用元素群运算符. 方程列写（1）先看Us对b,d点产生的等效电压Uoc，假定电流源开路，电桥电路可得（2）根据戴维南定理，Us的等效电流源的内阻应计算如下：设Us短路，求有b,d向网络看的阻抗，其等效电路如右图:电流源在b.d间产生的电压为Is*Zeq。（3）根据叠加定理根据以上这些公式，就可编写程序exn814。 程序exn814%按频率依次设定输入信号数组w=[eps,1,2];us=[10,10,0];Is=[5,0,5];%电抗分量是频率的函数，故自动成为数组z1=1./(0.5*w*j);z4=1*w*j;%对电阻分量也列写成常数数组z2=[2,2,2];z3=[2,2,2];%列出电路的复数方程uoc=(z4./(z3+z4)-z2./(z1+z2)).*us;zeq=z3.*z4./(z3+z4)+z1.*z2./(z1+z2);%列出等效阻抗u=Is.*zeq-uoc;%求解disp("wumphi")%显示disp([w",abs(u"),angle(u")*180/pi]) exn814运行结果运行这一程序的结果为：wumphi0.000010.000001.00003.1623-18.43492.00007.0711-8.1301由此我们可以写出u的表示式：u=10+10cos(t+18.4349)+7.0711cos(2t+8.1301) 例8-1-5交流电路矩阵建模如下图所示电路，设电阻R1=2Ω，R2=3Ω，R3=4Ω，感抗XL=2，容抗XC1=3，XC2=5，求各支路电流和电压 方程的建立解：建模：把原电路图中的电压源换成等效的电流源，则导纳均为两并联元件导纳之和，按照图示电源方向，其电流为列出a,b两点的电流方程这两个方程可写成的矩阵形式，并用AB求解。 程序exn815R1=2;R2=3;R3=4;XL=2;XC1=3;XC2=5;%给出原始数据us1=8,us2=6;us3=8;us4=15;%给出原始数据Y1=1/R1+1/(j*XL);%用复数表示各支路导纳Y2=1/R2-1/(j*XC1);Y3=1/R3-1/(j*XC2);A=[Y1+Y2,-Y2;-Y2,Y2+Y3];%列出ua,ub的系数矩阵AB=[us1/(j*XL)+us2/R1;us3/R3+us4/(-j*XC2)-us2/R2];%BU=AB;ua=U(1),ub=U(2)%求ua,ubI1=ua*Y1,I2=(ub-ua)*Y2,I3=ub*Y3,%求各支路的II1R=ua/R1,I1L=ua/(j*XL),I2R=(ub-ua)/R2,I2C=(ub-ua)/(-j*XC1),I3R=ub/R3,I3C=ub/(-j*XC2),H=compass([ua,ub,I1,I2,I3]);%画相量图 程序exn815执行结果ua=4.8845-0.5981iub=5.4874+2.5752iI1=2.1432-2.7413iI2=-0.8568+1.2587iI3=0.8568+1.7413iI1R=2.4422-0.2990iI1L=-0.2990-2.4422iI2R=0.2010+1.0578iI2C=-1.0578+0.2010iI3R=1.3718+0.6438iI3C=-0.5150+1.0975i 例8-1-6并联单调谐网络右图为一双电感并联单调谐网络，已知Rs=28.2kΩ，R1=2Ω，R2=3Ω，C=1000pF，L1=0.75mH，L2=0.25mH，求回路的通频带B及满足回路阻抗大于50kΩ的频率范围。例816的电路图 等效电路的建立解：◆建模先把回路变换为一个等效单电感谐振回路，把信号源的内阻rs变为并接在该单电感回路上的等效内阻rse，如右图所示。按照这个等效电路可写出如下的方程：图8-11例816的等效电路 电路方程令则有其他两支路的等效阻抗分别为（设s为拉普拉斯算子）总阻抗是这三个支路阻抗的并联谐振曲线可按ZE的绝对值直接画出。 程序exn816(1)r1=2;r2=3;L1=0.75e-3;L2=0.25e-3;C=1000e-12;rs=28200;L=L1+L2;r=r1+r2;rse=rs*(L/L1)^2;%折算内阻f0=1/(2*pi*sqrt(C*L))Q0=sqrt(L/C)/r,r0=L/C/r;%空载Q0值re=r0*rse/(r0+rse),%折算内阻与电阻并联Q=Q0*re/r0,B=f0/Q,%实际Q值和通带s=log10(w0);%设定计算的频率范围及数组f=logspace(s-.1,s+.1,501);w=2*pi*f 程序exn816(2)z1e=r1+j*w*L;z2e=r2+1./(j*w*C);%两个电抗支路的阻抗ze=1./(1./z1e+1./z2e+1./rse);%三个支路的并联阻抗%画对数幅频特性subplot(2,1,1),loglog(w,abs(ze)),gridaxis([min(w),max(w),0.9*min(abs(ze)),1.1*max(abs(ze))])%画相频特性subplot(2,1,2),semilogx(w,angle(ze)*180/pi)axis([min(w),max(w),-100,100]),grid%求幅特性大于50k的频带fh=w(find(abs(1./(1./z1e+1./z2e))>50000))/2/pi;fhmin=min(fh),fhmax=max(fh), 执行程序exn816所得结果谐振频率f0=159.15kH空载品质因数Q0=200等效信号源内阻rse=5.0133e+004考虑内阻后的品质因数Q=40.0853通频带B=3.9704e+003阻抗大于50kΩ的频率范围fhmin=157.7kHzfhmax=160.63kHz谐振频率附近的幅频和相频特性曲线见右图。 例8-1-7图示电路，R1=1Ω,R2=2Ω,C=0.5F,L=1H,求分别以uL与uC为输出时的频率响应。如把L换成容量为0.25F的电容，也求上述特性。解：◆建模MATLAB的一个优点是对同样结构的网络可以用统一的程序，如果只改变几个元件，可以用输入语句由用户来选择，我们就按这个办法来编本题的程序。 方程的建立先列出方程，设Z21，ZC2分别为L,C2的电抗，Z22为R22与C2串联的阻抗，Z2为Z21与Z22并联的阻抗。则有在分析频率响应时，要假设输入信号有很多频率成分，即ω或f是一个数组，因此MATLAB程序中所有与ω有关是量（例如Z,U,I）都应采用元素群运算的运算符。 程序exn817Clear,dw=0.1;w=[.2:dw:20];s=j*w;us=1;r1=1;r2=2;C2=0.5;L=1;z21=s*L;e=input("输入元件类型：电感，键入1；电容，键入2");ife==1L=input("输入电感量(H)");z21=s*L;elseife==2C1=input("输入电容量(F)");z21=1./(s*C1);elsedisp("元件类型错误，程序结束"),break,endzc2=(1./s*C2);z22=r2+zc2;z2=z21.*z22./(z21+z22)%串并联计算uL=us.*z2./(r1+z2);%分压计算电感上的电压uc=uL.*zc2./z22;%再分压计算电容上的电压subplot(2,2,1),loglog(w,abs(uL)),grid…%以下绘图语句略,注意subplot用法 程序exn817运行结果执行此程序，输入电感为1H，得出下图所示的频率响应和脉冲过渡过程曲线。换成电容，将得到另外的结果 例8-1-8关于网络参数的计算双口网络的计算公式本身并不复杂，只是公式多；包括复数和矩阵运算，因此用MATLAB可以带来很大方便。◆建模关于Z，Y，A，B，H，G六种网络参数之间的转换关系：这里本来应该有30种变换关系，但可以简化为三类，Z=inv(Y);Y=inv(Z);B=inv(A);A=inv(B);H=inv(G);G=inv(H);(2)A=[Z(1,1),det(Z);1,Z(2,2)]/Z(2,1);Z=[A(1,1),det(A);1,A(2,2)]/A(2,1);(3)H=[det(Z),Z(1,2);Z(2,1),1]/Z(2,2);Z=[det(H),H(1,2);H(2,1),1]/H(2,2);这三组关系是可从它们的定义得到的。有了这三类关系，这六种参数中任何两者之间就都能变换了。 实验和影像参数关于网络的实验和影像参数参数公式Zinf=A(1,1)/A(2,1);%负载阻抗为∞时的输入阻抗Zin0=A(1,2)/A(2,2);%负载阻抗为0时的输入阻抗Zoutf=A(2,2)/A(2,1);%信号源阻抗为∞时的输出阻抗Zout0=A(1,2)/A(1,1);%信号源阻抗为0时的输出阻抗Zc=sqrt(Zinf*Zin0);Zc=sqrt(Zoutf*Zout0)%Zc－特性阻抗γ=20*log10((sqrt(Zinf)+sqrt(Zin0))/(sqrt(Zoutf)-sqrt(Zout0)))%γ=α+jβ－传输常数实部α和虚部β分别为衰减常数（分贝）和相移常数（弧度）。都已包含在这个复数公式中，不必分别列写公式了。 例8-1-8双口网络数字例解：它的Z参数可以直接写出，然后求逆即可得Y。程序为r=100;L=0.02;C=0.01;w=300;z1=r;z2=j*w*L;z3=1/(j*w*C);Z(1,1)=z1+z2;Z(1,2)=z2;Z(2,1)=z2;Z(2,2)=z2+z3;Y=inv(Z),H=[det(Z),Z(1,2);Z(2,1),1]/Z(2,2),举一个简单的数字题，右图双口网络，r=100【欧姆】;L=0.02【亨利】;C=0.01【法拉】，频率w=300【1/秒】,求其Y参数及H参数。 8-2晶体管放大电路【例8-2-1】设将一个二极管与一个电阻串接，在这个电路的两端加上正向直流电压，如图8-15所示，试求出此电路中的电流Idx和电压Udx。 二极管正向特性及负载线二极管正向电流与电压的关系由下式确定其中I0——漏电流，设为10-12AK——玻尔茨曼常数，1.38×10-23T——绝对温度q——电子电荷，1.6×10-19负载电阻Rf中的电流Id1随电压Ud变化的关系为 二极管特性的计算和绘制%二极管特性k=1.38e-23;T=300;q=1.6e-019;Kt=k*T/q;Is=10e-12;Vd=0:0.01:3.5;Id=Is*(exp(Vd/Kt)-1);%[毫安]plot(Vd,Id),gridonaxis([0,max(Vd),0,100]),holdon%工作点的计算，先手工输入V0及RfId1=1000*(V0-Vd)./Rf;%[毫安]plot(Vd,[Id;Id1]),gridon[dI,nI]=min(abs(Id-Id1));Vdx=Vd(nI);Idx=Id(nI);disp("Vdx,Idx="),[Vdx,Idx],holdoff 例8-2-2放大器低频等效电路典型放大器低频等效电路如右图，其元件参数为：C1＝10μF,Rs=100Ω,Rb=10kΩ,hie=1000Ω,hfe=100,Re=200,Ce=100μF,Rc=1000Ω,C2=10μF,RL=2000Ω要求探讨C2,Ce对幅频特性的影响。图8-16典型放大器低频等效电路 方程组列写解：先用节点电位法列写其方程，设u1,u2,u3,u4如图，可列出其四个KCL方程如下：整理乘矩阵形式（注意其中s为拉普拉斯算子） 化为矩阵方程及其解写成a*U=b故U=zb给定输入us=1，和一个频率ω,从这个方程组就可解得输出的复数解x,它的四个分量分别为u1,u2,u3,u4。 程序exn822(1)w=logspace(0,3);%规定频率范围及数组值C1=1e-5;rs=100;rb=1e4;%给元件赋值hie=1000;hfe=100;us=1;re=200;Ce=1e-4;rc=1000;C2=1e-5;rL=2000;forC2=[C2,10*C2]%对C2及10*C2分别计算forCe=[Ce,10*Ce]%对Ce及10*Ce分别计算fori=1:length(w)%对各个频率计算各点输出s=j*w(i); 程序exn822(2)a11=1/rs+s*C1;a12=-s*C1;%给a矩阵元素赋值a21=-s*C1;a22=s*C1+1/rb+1/hie;a23=-1/hie;a32=(1+hfe)/hie;a33=-((1+hfe)/hie-1/re+s*Ce);a42=hfe/hie;a43=-hfe/hie;a44=-(1/rc+s*C2./(rL*C2*s+1));a=[a11,a12,0,0;a21,a22,a23,0;0,a32,a33,0;0,a42,a43,a44];b=[us/rs;0;0;0];%给b矩阵元素赋值x=ab;u(:,i)=x;%求与第i个频率对应的输出电压ends1=j*w;uL=u(4,:).*rL./(rL+1./(C2*s1));%求负载电压loglog(w,abs(uL)),grid,holdon%绘对数幅频特性图endend 程序exn822的执行结果。可以看出，在所给的参数下，把C1加大10倍可把整个低频区的幅频特性提高将近10倍，而把Ce加大10倍则只能在低频区的高端提高其幅频特性。 例8-2-3运算放大器分析电路如图8－18所示，试分析放大器开环增益和频率响应对整个电路闭环频率响应的影响，并绘出曲线。解◆建模：设运算放大器的开环增益为A，它是频率的函数，则在图示的连接方法下，闭环输出与输人电压之比为运算放大器等效电路 电路方程的建立（1）（1）在增益A很大时，分母上的第二项可以忽略不计，因而得出理想运放的闭环传递函数（2）式中的s为拉普拉斯算子，将它换成jω，就得出频率响应，所以这两个式子都是复数方程。根据题意，要考虑A＝A（ω）对H（ω）的影响，计算将十分冗繁。利用MATLAB可以方便快速地解决这个问题，但必须给出具体数据。通常，运算放大器的开环传递函数中包括三个实极点，即 电路方程的建立（2）其中ωl＜ω2＜ω3，取负号后为其三个极点，A0为直流增益。为了避免自激，通常使ωl和ω2差得很大，例如ωl＜5001／s，ω2＞1061／s，而且ω2和ω3也要拉开，现设ωl＝500，ω2＝2×106，ω3＝5×107，并设Z1＝2kΩ，Z2取三种值：2okΩ、100kΩ和500kΩ，求其H（ω）并绘出曲线。 程序exn823％运算放大器有限增益和频率响应对电路特性的影响Z2=[20,100,500]*1000;Z1=2000;%设定元件参数%按提示从键盘输入A0,w1,w2,w3w=logspace(2,8);%设定频率数组b=A0*w1*w2*w3;a=poly([-w1,-w2,-w3]);%系数向量A=polyval(b,j*w)./polyval(a,j*w);%放大器开环频率响应fori=1:3%循环计算三种Z2的闭环响应Z12(i)=Z2(i)/Z1;H(i,:)=-Z12(i)./(1+(1+Z12(i))./A);%放大器闭环响应%Hdb=20*log10(abs(H));%化为分贝semilogx(w,abs(H(i,:)),"linewidth",2)%画出频率-增益曲线holdonend% 程序exn823运行结果运行这一程序得到如图所示的曲线，可以看出，此运放在低频区较宽的一个频带内具有平坦的增益Z2／Z1。但在高频区却出现了谐振峰，这也就容易造成运算放大器的自激现象。 8-3电力电子和电机例8-3-1一个可控硅全波整流器，计算负载上得到的有效值电压与点火角(1到180度)的函数关系,并画出曲线。解：◆建模因为是全波整流，只要研究半个波形即可，其关键是如何用向量表示不连续波形。周期为T的电压的有效值定义为这里用的周期是半波，即相角φ＝ωt,取π作为周期T。将t分成180份，来表达可控硅负载电压波形，如图8－21所示。对应于程序中的waveform数组，它前一段为0，后一段为正弦波，对该数组先进行元素群平方运算，相加平均，再做开方运算，便可得到有效值。 程序exn831(1)wt=[1:180]*pi/180;%把半波分割为180份volts=220*sqrt(2)*sin(wt);%完整的半波波形forii=1:180%求不同点火角ii时的波形有效值%求不同点火角ii时的波形waveform=[zeros(1,ii-1),volts(ii:180)];ifii==45%记录点火角为45度时的波形waveform45=waveform;endtemp=sum(waveform.^2);%计算各点波形的平方积分：rms(ii)=sqrt(temp/180);%计算积分的均方根：end%画负载上的有效值电压与点火角关系曲线：plot([1:180],rms,"Linewidth",2.0); 程序exn831(2)xlabel("bf点火角（度)");%下一条语句可在图上作标签标注legend("bf负载电压有效值(V)");gridon;%画点火角45度时负载上的电压波形：figure(2),plot(wt,waveform45,"Linewidth",2.0);%下一条语句可标注希腊字母xlabel("bfomegaittrm(弧度)");ylabel("bf负载电压");gridon; 程序exn831运行结果 例8-3-2三相电机旋转磁场感应电动机的定子由三组空间上相差120度的绕组和磁极构成，如图8-23的aa’、bb’、cc’所示。在三个绕组上依次加有120度相位差的励磁电流，就可以形成一个在空间旋转的磁场。 编写程序exn832的思路利用MATLAB来演示这一过程特别有效：利用MATLAB的复数功能，描述三个磁极在空间不同方向产生的磁场；利用时间数组来描述三个绕组中电流和磁场的相位变化；把三个磁场作向量相加，即可求得合成磁场；利用MATLAB的绘图和动画功能显示磁场的运动。根据这个思路来编写MATLAB的程序较为容易。 程序exn832(1)I=10;freq=50;w=2*pi*freq;%50Hz角速度(rad/s)t=0:1/5000:.2/50;Ia=I*sin(w*t);Ib=I*sin(w*t-2*pi/3);Ic=I*sin(w*t+2*pi/3);%建立三个分量磁场的表达式：kmag=1/I;%把最大磁场归一化为1Baa=kmag*Ia*(cos(0)+j*sin(0));%括号中的项表示A磁场空间方向为0度Bbb=kmag*Ib*(cos(2*pi/3)+j*sin(2*pi/3));%B磁场空间方向为120度Bcc=kmag*Ic*(cos(-2*pi/3)+j*sin(-2*pi/3));%C磁场空间方向为-120度Bnet=Baa+Bbb+Bcc;%计算合成磁场%分别画出合成磁场Bnet和三相磁场Baa,Bbb,Bcc的矢量幅值和方向，%Bnet为红色，Baa为黑色，Bbb为蓝色，Bcc为品红色。 程序exn832(2)forii=1:length(t)plot(Bnet,"k");%画出合成磁场向量端点holdon;%画出四个磁场相量，其合成磁场则成为旋转向量plot([0real(Baa(ii))],[0imag(Baa(ii))],"k","LineWidth",2plot([0real(Bbb(ii))],[0imag(Bbb(ii))],"b","LineWidth",2);plot([0real(Bcc(ii))],[0imag(Bcc(ii))],"m","LineWidth",2);plot([0real(Bnet(ii))],[0imag(Bnet(ii))],"r","LineWidth",3);axissquare;axis([-22-22]);drawnow;holdoff;end 程序exn832运行结果执行此程序，将得到一个演示旋转磁场的动画，右图给出了其中一个画面。Baa,Bbb,Bcc表示三个方向固定，在空间上夹角为120度的磁场，它们的大小和正负号按交流电流的正弦波变化，相位也互差120度，三者的向量和就形成了一个在空间旋转的磁场。 一些编程技巧在程序中要注意drawnow的用法，通常MATLAB采用先计算，后画图的顺序，在程序中即使出现画图命令，它也只把数据存起来，作好画图准备，继续进行计算，直到程序暂停或结束时才统一画图。在显示动画时，这种做法就不行了，必须用drawnow命令把计算的结果立即画出。这样做程序执行的速度将大大下降。在编动画程序时还要注意的是holdon和holdoff命令放置的位置。 例8-3-3感应电动机机械特性解：◆建模感应电动机中任一相的等效电路如右图(a)，其中S为转差率。再用戴文宁定理依次等效为(b),(c)，根据(c)图列写方程如下： 方程的建立由最后的等效电路，可得消耗在转子回路中的总功率（三相功率总和）电磁转矩与同步角速度的乘积等于电磁场功率，故有 程序exn833(1)clear,fvolt=50,%电源频率【Hz】%定子相绕组电阻和电抗r1=0.641;x1=1.106;z1=r1+j*x1;%转子等效电阻和电抗r2=0.332;x2=0.464;z2=r2+j*x2;%磁化支路激励损耗等价电阻和支路电抗rm=2.5;xm=26.3;zm=rm+j*xm;vph=380/sqrt(3);%相电压(v)p=2,nsync=fvolt/p*60;%同步转速(r/min)%（p=2,双极电机）wsync=nsync*2*pi/60;%同步角速度(rad/s)%计算A,B两点之间电压vab和阻抗zabvab=vph*zm/(z1+zm);zab=zm*z1/(z1+zm); 程序exn833(2)forr2=[r2,2*r2]%求两种内阻的电机特性s=(eps:1:50)/50;%转差率数组,第一点避开0nm=(1-s)*nsync;%电机转速数组z2e=r2./s+j*x2;%转子等效负载I2e=vab./(zab+z2e);%转子等效电流P2e=3*abs(I2e.^2*r2./s);%三相电磁功率总和%转矩等于电磁功率除以同步角速度torque=P2e/wsync;%画机械特性曲线plot(nm,torque,"LineWidth",2.0);holdon;end 程序exn833运行结果程序运行后,将得出图8-3-6所示的转矩转速特性. 8-4高频电路无损耗同轴线的特性阻抗。设无损耗同轴线内导体半径为a，外导体内半径为R,内外导体间的媒质参数为（ε,μ,σ），求其特性阻抗及绘出它随ε变化的曲线。解：◆建模根据电磁场理论可知无损耗同轴线单位长度的电感和电容分别为：故其特性阻抗为通常同轴线内外导体间的媒质为绝缘电介质（例如聚乙烯、聚四氟乙烯），其参数为μ=μ0,ε=ε0εr，其中εr为相对介电常数，因为μ0/ε0=1.42×105，故得 程序exn841％取常用于传输有线电视信号的同轴线为例，设a=0.5mm,b=4mm,a=0.5;b=4;%设定相对介质常数范围er=linspace(1,20);z0=60*log(4/0.5)./sqrt(er);plot(er,z0);gridxlabel("相对介电常数"),legend("特性阻抗（欧姆）") 程序exn841运行结果见右图。通常电视传输同轴线的特性阻抗标准为50欧姆，由此可确定要求的介质常数。 例8-4-2Smith圆图命题：用MATLAB语言编程画史密斯(Smith)圆图解:◆建模Smith图是在高频工程中常常用到的。它把归一化复阻抗z映射为复反射系数γ:γ=(z-1)/(z+1)=u+iv其中z=r+i*x.Smith图的横坐标是γ的实部u而纵坐标是它的虚部v。指定参数r=常数及x=常数得到圆的轨迹，由此图可以根据γ来求r及x，也可由r及x求得反射系数u和v，可先把γ的复数方程化为两个实数方程，其结果为： 方程的建立，固定r,变化x(消去x)的轨迹固定x,变化r(消去r)的轨迹这两个都是圆的方程，可找出其圆心和半径，以圆心角为参数画出圆。 程序exn842(1)plot([00],[-1.1+1.1],"r"),holdon,xlabel("u")%画坐标轴系plot([-1.1+1.1],[00],"r"),ylabel("v"),axisequal,axis([-1.1,1.1,-1.1,1.1]),gridtr=2*pi*(0:.01:1);%指定所要画的圆的圆周角分度数组forr=[0,.2,.5,1,2,5]%指定所要画的r=常数的曲线rr=1/(r+1);cr=1-rr;plot(cr+rr*cos(tr),rr*sin(tr))%画等r圆end 程序exn842(2)forx=[.2,.5,1,2,5]%指定你所要画的x=常数的曲线rx=1/x;cx=rx;tx=2*atan(x)*(0:.01:1);plot(1-rx*sin(tx),cx-rx*cos(tx))%画等x圆,x>0plot(1-rx*sin(tx),-cx+rx*cos(tx))%画等x圆,x<0end 程序exn842的运行结果执行程序的结果见右图。其上的参数可用gtext命令用鼠标标注，免去确定坐标的麻烦。实际上，利用MATLAB的复数运算功能，也可以省去把复数方程化为实数方程的推导，直接用上述复数方程，分别设定参数r和x，按gamma的实部和虚部绘图即可。 用复数方程画Smith圆图的程序p=linspace(100,0.01,500);x=[-p,p];q=[eps,0.05,0.10.2,0.5,1,2,5,10];forr=qz=(r+i*x-1)./(r+i*x+1);plot(z),holdon,axisequalendr=p;forx=[-q,q]z=(r+i*x-1)./(r+i*x+1);plot(z),holdon,axisequalendgrid,holdoff 程序exn842a的运行结果程序ex842a.m.核心的语句是：z=(r+i*x-1)./(r+i*x+1);plot(z)其主要难度是r和x数组不太好设定，设得不好,画出的圆会疏密不匀。运行此程序可得右图。 '