神经网络诊断原理教学课件PPT 34页

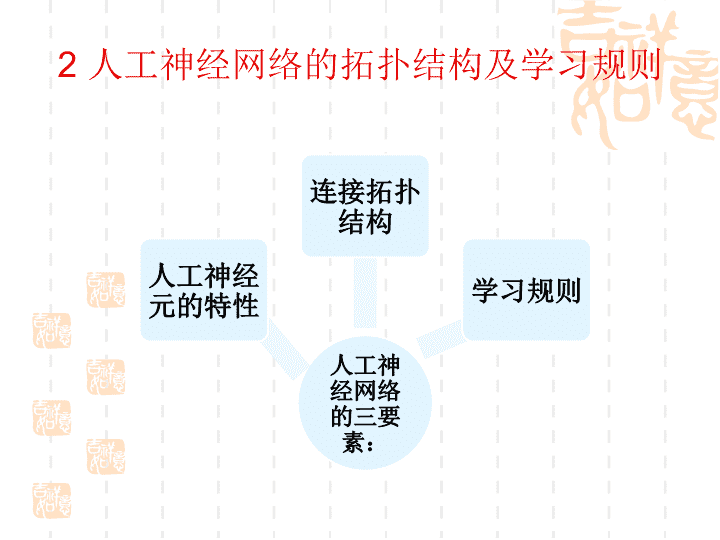
'神经网络诊断原理概述人工神经网络的拓扑结构及学习规则多层前向神经网络模型及BP算法径向基函数（RBF）网络及其学习算法模糊神经网络模型无监督神经网络模型 1概述人工神经网络在故障诊断领域的主要应用方面：从模式识别角度应用神经网络作为分类器进行故障诊断；从预测角度应用神经网络作为动态预测模型进行故障诊断；从知识处理角度建立基于神经网络的诊断专家系统。 2人工神经网络的拓扑结构及学习规则人工神经网络的三要素：人工神经元的特性连接拓扑结构学习规则 2.1生物神经元与人工神经元模型为阈值为神经元的激活水平为权重神经元的激活函数 神经元模型的数学描述（7.1）(7.2) 2.2人工神经网络的拓扑结构不含反馈的前向网络它包括三个单层的输入层、隐含层和输出层。应用：多层感知器（MLP）、误差反向传播算法（BP算法）反馈网络特点：具有相当丰富的动态特性，从某一初始状态开始，网络需经过若干次的状态变化，才能到达某种平衡状态应用：贺蒲费特（Hopfield）网络、全互联网络等 图人工神经网络的拓扑结构a前向神经网络b全互联网络c输出反馈网络d状态反馈网络 2.3人工神经网络的学习规则人工神经网络最有价值的特性是它的自适应能力，而这种能力是通过学习或训练实现的。学习规则类别：有指导学习如纠错规则，随机学习规则无指导学习如相关规则，竞争学习规则强化学习特别指出，在工程实践中，上述学习方法并不是相互冲突的，可以相互融合。 3多层前向神经网络模型及BP算法3.1BP网络模型BP网络的故障诊断模型利用的是BP网络的泛函逼近能力。既一个具有任意压缩型激活函数的单隐层前向网络，只要有充分多的隐层单元，就可以以任意精度逼近任意一个有限维的波莱尔可测函数。对多层次前向网络：（7.3）注意：不能为线性函数，否则整个网络只相当于一个单层网络。 3.2BP算法BP算法1、BP算法的基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成，以实现网络输出和期望输出间的均方误差最小化。1）正向传播：输入样本－>输入层－>各隐层（处理）－>输出层注：若输出层实际输出与期望输出（教师信号）不符，则转入2）（误差反向传播过程）2）误差反向传播：输出误差（某种形式）－>隐层（逐层）－>输入层其主要目的是将误差信号沿原来的连接通路返回，修改各层的权重，使得误差信号最小。 对单样本学习的BP算法由推到可知第L-1层的信号误差是由输出层的误差信号经输出层权重反向传播计算所得。（7.11）（7.12）为学习率；为L-1层的输出矢量；为误差信号。对多样本学习问题有两种处理方法:1模式（样本）学习法2批处理学习法其中批处理学习法的速度通常快于模式学习法。 BP网络存在的不足：1)训练速度过于缓慢；2)存在局部极小问题，难以发现最佳权重解;3)网络结构的确定缺乏严格的理论依据，通常依据经验：4)存在“突然遗忘”现象。针对以上不足，产生了各种不同的改进的BP算法。 3.3BP网络分类性能分析最成功的的应用之一是应用于模式识别问题。BP网络的功能主要是：隐层单元的非线性带来的。一般在应用中，BP网络不需要超过两个隐层就能形成任意复杂形状的决策区域。BP网络是通过超平面实现对空间划分的，因此要求有完备的训练样本集，否则极易给出错误的结论。此外，BP网络的推广能力还缺乏有效的判别证据。 4径向基函数（RBF）网络及其学习算法RBP网络模型RBP网络是解决BP诸多问题的最有效方案之一，具有最佳逼近特性。RBP通常是一种两层前向网络如图： RBP和BP相比有着本质的不同：局部接受域形状；局部权重可调；决策时隐含了距离的概念。RBP网络最常用的非线性激活函数为高斯函数 是RBF网络的输入数据向量；是第j个隐含层节点的输出；是高斯核函数的中心值；h为隐含层RBF节点数；为半径。输出分布符合3原则。注：影响RBP网络性能的关键因素是基函数中心的选取而非所采用的的非线性激活函数的形式。 4.2RBP网络学习算法学习过程：1）确定每个RBP网络单元的中心和半径；2）调节权矩阵W。4.2.1中心的确定常用的为K-均值算法具体过程为：1）初始化所有的聚类中心；2）如果则将样本划归到i类。3计算各类样本的均值 式中为第j类的样本数。4）重复步骤2）和3）直至所有聚类中心不在变化。获得各个聚类中心后就可赋给各RBP单元作为RBP的中心。 4.2.1半径的确定半径决定了RBP单元接受域的大小，对网络的精度有极大的影响。选取的基本规则是使得所有RBP单元的接受域之和覆盖整个训练样本空间。通常有两种选取方法。一种是应用K均值聚类算法后另一种方法是对每一个中心求取它与其邻近的N个单元中心距离的平均值作为半径。通常课取N=1。 4.2.3调节WW的调节通常有两种方法：（1）线性最小二乘法即令网络输出，U为目标矢量，则（2）梯度法迭代公式为RBP网络另一种有效的学习算法是正交最小二乘算法（OLS）。（只调节权重W对RBP选取要求较高） 5模糊神经网络模型5.1一般概念模糊神经网络（FNN）是模糊系统和神经网络相结合的产物。根据侧重点不同可分为：利用神经网络的自适应和函数逼近功能，提高模糊系统的自适应能力，提高精度。利用模糊系统增强神经网络的信息处理能力。神经网络和模糊系统协同工作。将模糊系统引入传统神经网络的学习过程，提高学习速度。 构造FNN的方法：（1）传统神经网络的模糊化可分为全部模糊化和部分模糊化。（2）基于模糊类型的FNN可分为直接和模糊系统结构相连的构造法和基于模糊基函数（FBF）的概念构造网络。 5.2FBF及FBF网络5.2.1FBF一般具有重心非模糊化算子的模糊基函为若应用单点模糊法则从而 5.2.2FBF网络模糊系统可以表示成一系列FBF的线性组合及模糊系统的输出为式中H为模糊基函数的个数即模糊系统的规则总数。 FBF函数为高斯基函数的非线性组合，不仅能够处理数值信息，而且还能够处理语义信息。 5.4FBF网络学习算法下形式 又故FBF网络需要学习的参数也为权重，中心及半径，其算法和RBP网络的算法相同。注：FBF规则一般需要优化，一般通过规则相似度量和重要性度量优化网络结构。 6无监督神经网络模型在无监督学习中，输入数据的冗余性提供了知识，并且无监督学习的计算复杂性较小，学习较快，但没有有监督学习分类准确。 6.1无监督Hebb学习方法任务：根据p(X)产生的足够多样本对网络进行训练，使网络再输入模式X时，输出y能够反映输入X与整体样本的相似性。应用Hebb学习规则时，权向量大小不稳定，为解决此问题，采用修正的Hebb规则：1)2) 当权重不再调节时，对于Hebb规则趋于X的均值；对于修正的Hebb2)规则对于Hebb和修正的Hebb规则，其权解的最终放向与输入的相关阵C的最大特征值所对应的特征向量的方向一致或相反。 6.2无监督竞争学习“胜者为王”的学习规则图竞争网络的结构a一般竞争结构b一种前向匹配竞争网络 即当获胜时，调节权重使节点j以更大的可能性获胜即再输入节点j所受刺激变为上述调节，存在权重无限增长的缺陷，故权重规一化即令也可只对和获胜节点的权矢量进行调节。 '