- 554.00 KB
- 2022-04-29 14:46:22 发布
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
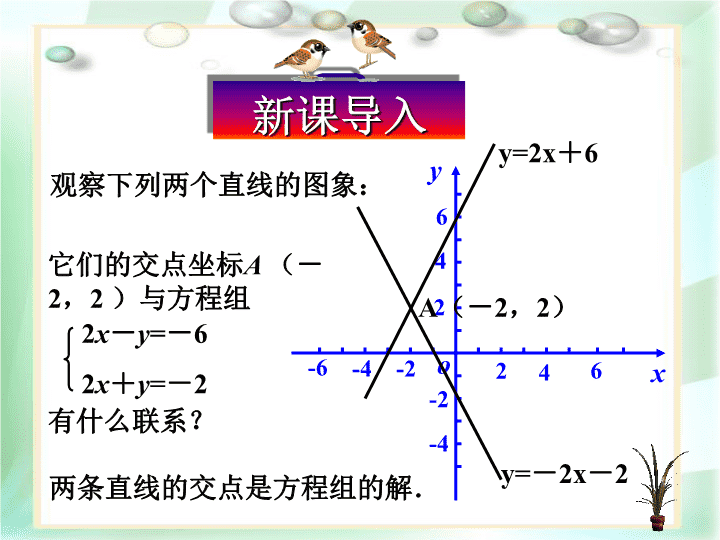
'观察下列两个直线的图象:-6o-446246-2-2-4xy2y=-2x-2A(-2,2)y=2x+6它们的交点坐标A(-2,2)与方程组有什么联系?2x-y=-62x+y=-2两条直线的交点是方程组的解.新课导入
人教版·数学·八年级(下)一次函数与二元一次方程组阳光初中八年级数学备课组
复习:以二元一次方程的解为坐标的点都在相应的函数图象上.反过来,一次函数图象上的点的坐标都适合相应的二元一次方程.
一、创设情境,导入新课问题:1号探测气球从海拔5m处出发,以1m/min的速度上升,上升了1h.```(1)请用式子表示1号探测气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系.
一、创设情境,导入新课问题:1号探测气球从海拔5m处出发,以1m/min的速度上升,上升了1h.(2)请写出函数y=x+5的图象上的任意5个点的坐标,你写出的5个点的坐标是否都满足方程y-x=5?你是怎么验证的?
一、创设情境,导入新课问题:1号探测气球从海拔5m处出发,以1m/min的速度上升,上升了1h.(3)以方程y-x=5的所有解组成的坐标是否都在一次函数y=x+5的图象上?Zxxk
二、深入剖析,感悟新知思考:通过问题(2)、(3)的分析,我们能否概括出二元一次方程的解和一次函数图象上的点的坐标之间是什么关系?Zxx```k方程的解一次函数图象上点的坐标以二元一次方程的解为坐标的点,它都在其相应的一次函数的图象上;一次函数图象上点的坐标,都适合其相应的二元一次方程.
问题:1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.(1)请用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系;二、深入剖析,感悟新知
问题:1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.(2)在某一时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?二、深入剖析,感悟新知在同一直角坐标系内分别画出一次函数y=x+5和y=0.5x+15的图象(如右图).
问题:1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.(2)在某一时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?二、深入剖析,感悟新知你能读出这两个图象的交点坐标吗?
问题:1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.(1)请用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系;二、深入剖析,感悟新知
方程组的解和它对应的两条直线的交点坐标有什么关系呢?二、深入剖析,感悟新知方程组的解直线上点的坐标.
观察下列两个直线的图象:-6o-446246-2-2-4xy2y=-2x-2A(-2,2)y=2x+6它们的交点坐标A(-2,2)与方程组有什么联系?2x-y=-62x+y=-2两条直线的交点是方程组的解.解决问题
例1当自变量x取何值时,函数y=2.5x+1和y=5x+17的值相等?这个函数值是多少?Zx`````xk三、例题学习,提高认知方法一:联立两个函数,得2.5x+1=5x+17,解此方程;方法二:把两个函数转化为二元一次方程组,解方程组;方法三:画函数图象,求交点坐标.
八年级数学第十四章函数14.3用函数观点看方程(组)与不等式一次函数与二元一次方程组例2一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间记费;方式B除收月基费20元外再以每分0.05元的价格按上网时间记费。如何选择收费方式能使上网者更合算?
练习1:如图,若直线l1与l2相交于点P,则根据图象可得,二元一次方程组的解是________.练习2:两条直线y=k1x+b1和y=k2x+b2相交于点A(-2,3),则方程组的解是()
【总结提升】用图象法确定二元一次方程组的解(1)将两个方程都化为y=kx+b(k,b是常数,k≠0)的形式.(2)画出两个函数的图象,确定交点坐标.(3)两个一次函数图象交点的坐标是这个二元一次方程组的解.
246880160X/n轮船快艇Y/km练习3:如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象,根据图象解答下列问题:(1)分别求出表示轮船和快艇行驶过程的函数表达式(2)轮船和快艇在途中行驶的速度是多少?(3)快艇出发多长时间追上轮船?此时距离出发地多少千米?
练习4:某单位急需用车,但不准备买车,他们准备和一个个体车主或者一国有出租车公司其中一家签订合同.设汽车每月行使x千米,应付给个体车主的约费用y1元,应付给出租车公司的约费用为y2元,y1,y2分别与x之间的函数关系如下图所示,每月行程等于多少时,租两家车的费用相同,是多少元?行程为多少时租用个体户车便宜?行程为多少时租用出租车公司的车便宜?y1y2X/kmY/元15001000
练习5:如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为.【解析】把y=2代入y=x+1,得x=1,∴点P的坐标为(1,2),根据图象可知当x≥1时,y=x+1的函数值大于y=mx+n相应的函数值.因而不等式x+1≥mx+n的解集是:x≥1.答案:x≥1
练习6:兄弟俩赛跑,开始前,弟弟在哥哥前方9m,已知弟弟每秒跑3m,哥哥每秒跑4m,列出函数关系式,画出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?
归纳总结:从数的角度看:从形的角度看:求二元一次方程组的解x为何值时,两个函数的值相等求二元一次方程组的解是确定两条直线交点的坐标一次函数与二元一次方程组
作业:必做:补充作业本45页1、2、3、4题选做第5题
必:1:如图,已知一次函数y=ax+b和正比例函数y=kx的图象交于点P,则根据图象可得二元一次方程组的解是_____.
2x+y=42x-3y=12必做2:用图象法解方程组:①②解:由①得:由②得:作出图象:观察图象得:交点(3,-2)∴方程组的解为x=3y=-2xoyy=-2x+4y=2/3-4
选做1:如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,假设两种灯的使用寿命是2000h,照明效果一样.(1)根据图象分别求出l1,l2的函数解析式.(2)当照明时间为多少时,两种灯的费用相同?(3)当照明时间为多少时,白炽灯费用少?当照明时间为多少时,节能灯费用少?
【解析】(1)设直线l1的解析式为y1=k1x+2,由图象得:17=500k1+2,解得:k1=0.03,∴y1=0.03x+2(0≤x≤2000),设直线l2的解析式为y2=k2x+20,由图象得:26=500k2+20,解得:k2=0.012,∴y2=0.012x+20(0≤x≤2000).
选做2:已知两直线y1=2x-3,y2=6-x,(1)在同一坐标系中作出它们的图象.(2)求它们的交点A的坐标.(3)根据图象指出x为何值时,y1>y2;x为何值时,y1
您可能关注的文档
- 语文人教版三年级下册女娲补天课件PPT.ppt
- PEP人教版小学五年级下册英语Recycle 1课件PPT.ppt
- 《汉语拼音11 ie üe er》教学课件PPT.ppt
- 北京话课件PPT下载 教科版五年级语文下册课件.ppt
- 北师大版小学一年级下册数学《买衣服》课件PPT.ppt
- 人教版四年级《全神贯注》课件PPT.ppt
- 鲸课件PPT版.ppt
- 语文人教版三年级下册《七颗钻石》课件PPT.ppt
- 人教版四年级语文下册《永生的眼睛》课件PPT.ppt.ppt
- 《1922一次函数(应用)(4)》课件PPT(人教版八年级上).ppt
- 语文人教版五年级下册景阳冈课件PPT.ppt
- 七色花课件PPT版.ppt
- 语文人教版五年级下册自己的花是让别人看的课件PPT.ppt
- 语文人教版五年级下册课件PPT.ppt
- 人教版语文四年级上册《去年的树》课件PPT.ppt
- 穷人课件PPT.ppt
- 语文人教版三年级上册《花钟》课件PPT.ppt
- 应用文 便条 请假条留言条 课件PPT.ppt