数学分析课件PPT课件.ppt 32页

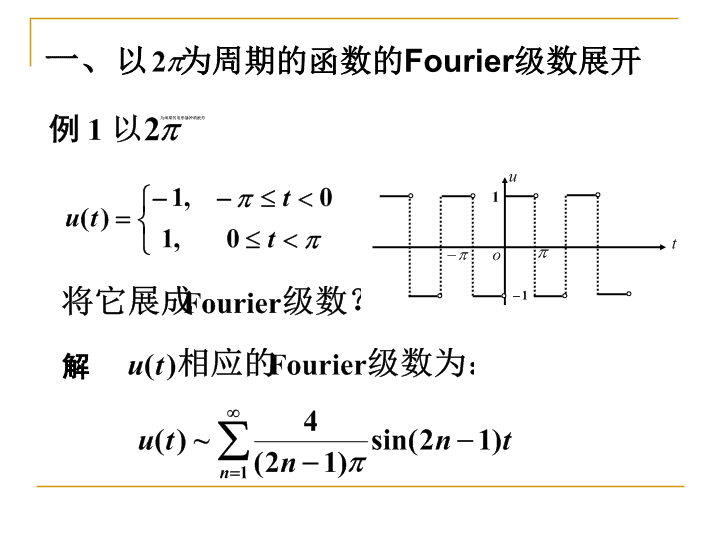
'§12.3函数的Fourier级数展开 一、以为周期的函数的Fourier级数展开解 所以函数的傅氏展开式为：和函数图象为 注意:对于非周期函数,如果函数只在区间上有定义,并且满足收敛定理条件,也可展开成傅氏级数.作法: 解所给函数满足Dini定理条件. 所以 利用傅氏展开式求级数的和 二、正弦级数与余弦级数1.奇函数和偶函数的傅里叶级数定理 证明奇函数 同理可证(2)定义偶函数 解所给函数满足Dini定理条件, 和函数图象 2.函数展开成正弦级数或余弦级数常用如下两种情况 奇延拓: 偶延拓: 解(1)求正弦级数. (2)求余弦级数. 三、以2L为周期的傅氏级数 其中 则有则有 解 解 另解 作业：习题11.31(1),3).4.(2),(3)6,7作业二：Fourier的收敛的条件是什么？怎样得到的？'