最新14.2.1全等三角形的判定(SAS)课件PPT.ppt 61页

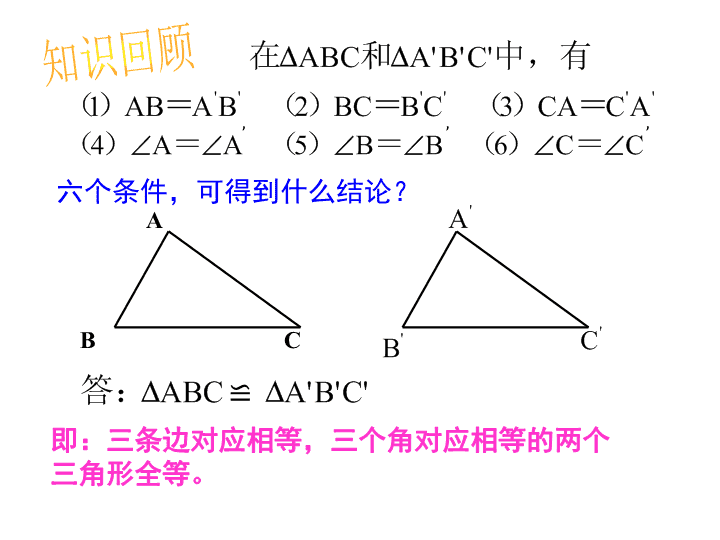
'14.2.1全等三角形的判定(SAS) 知识回顾ABC1.什么叫全等三角形？能够重合的两个三角形叫全等三角形。2.全等三角形有什么性质？全等三角形的对应边相等，对应角相等。3、如图∆ABC≌∆A’B’C’，说出两个三角形中的对应线段、对应角？ ABC知识回顾即：三条边对应相等，三个角对应相等的两个三角形全等。六个条件，可得到什么结论？≌’’’ 三个条件呢？探究活动三个角；2.三条边；3.两边一角；4.两角一边。如果给出三个条件画三角形，你能说出有哪几种可能的情况？ 结论:三个内角对应相等的三角形不一定全等。探究活动有三个角对应相等的两个三角形60o30030060o90o90o三个条件呢？ 尺规作图，探究边角边的判定方法问题1先任意画出一个△ABC，再画一个△A′B′C′，使A′B′=AB，∠A＇=∠A，C′A′=CA（即两边和它们的夹角分别相等）．把画好的△A′B′C′剪下来，放到△ABC上，它们全等吗？ABC ABCA′DE尺规作图，探究边角边的判定方法现象：两个三角形放在一起能完全重合．说明：这两个三角形全等．画法：（1）画∠DA′E=∠A；（2）在射线A′D上截取A′B′=AB，在射线A′E上截取A′C′=AC；（3）连接B′C′．B′C′ 几何语言：在△ABC和△A′B′C′中，∴△ABC≌△A′B′C′（SAS）．尺规作图，探究边角边的判定方法归纳概括“SAS”判定方法:两边和它们的夹角分别相等的两个三角形全等（可简写成“边角边”或“SAS”）．AB=A′B′，∠A=∠A′，AC=A′C′， 课堂练习下列图形中有没有全等三角形，并说明全等的理由．甲8cm9cm丙8cm9cm8cm9cm乙30°30°30° 课堂练习图甲与图丙全等，依据就是“SAS”，而图乙中30°的角不是已知两边的夹角，所以不与另外两个三角形全等．甲8cm9cm丙8cm9cm8cm9cm乙30°30°30° 已知：如图，AD∥BC，AD=CB求证：△ADC≌△CBA分析：观察图形，结合已知条件，知，AD=CB，AC=CA，但没有给出两组对应边的夹角（∠1，∠2）相等。所以，应设法先证明∠1=∠2，才能使全等条件充足。AD=CB（已知）∠1=∠2（已证）AC=CA（公共边）∴△ADC≌△CBA（SAS）例1:证明：∵AD∥BC∴∠1=∠2（两直线平行，内错角相等）在△DAC和△BCA中DC1AB2B范例学习 例2:因铺设电线的需要，要在池塘两侧A、B处各埋设一根电线杆（如图），因无法直接量出A、B两点的距离，现有一足够的米尺。请你设计一种方案，粗略测出A、B两杆之间的距离。。AB范例学习 小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结DE，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。AC=DC∠ACB=∠DCEBC=EC∴△ACB≌△DCE∴AB=DE在△ACB和△DCE中 BCDEA例3：如图，已知AB＝AC，AD＝AE。求证：∠B＝∠CCEABAD证明：在△ABD和△ACE中∴△ABD≌△ACE（SAS）∴∠B＝∠C（全等三角形对应角相等）范例学习 例4：已知：如图，AB=CB，∠ABD=∠CBD△ABD和△CBD全等吗？分析:△ABD≌△CBD边:角:边:AB=CB(已知)∠ABD=∠CBD(已知)？ABCD(SAS) 例5：已知：点A、E、F、C在同一条直线上，AD=CB，AD∥CB，AE=CF.求证：EB∥DFADBCEF证明：∵AD∥CB（已知）∴∠A=∠C（两直线平行，内错角相等）∵AE=CF（已知）∴AE+EF=CF+EF（等式的性质）即AF=CE在△AFD与△CEB中AF=CE（已证）∠A=∠C（已证）AD=CB（已知）∴∴△AFD≌△CEB（SAS）∴∠AFD=∠CEB∴EB∥DF FEDCBA例6：如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与　△FED全等吗？为什么？解：全等。∵BD=EC（已知）　　　∴BD－CD＝EC－CD。即BC＝ED在△ABC与△FED中∴△ABC≌△FED（SAS）AC∥FD吗？为什么？∴∠1＝∠2（　）∴∠3＝∠4（　）∴AC∥FD（内错角相等，两直线平行）4321ïîïíìÐÐ（已证）＝（已知）＝（已知）＝EDBCEBEFAB 例7.(1)如图，AC=BD，∠CAB=∠DBA，你能判断BC=AD吗？说明理由。ABCD证明:在△ABC与△BAD中AC=BD∠CAB=∠DBAAB=BA∴△ABC≌△BAD（SAS）(已知)(已知)(公共边)∴BC=AD（全等三角形的对应边相等） (2).如图，在△AEC和△ADB中，已知AE=AD，AC=AB请说明△AEC≌△ADB的理由。AE=AD(已知)=()AC=AB(已知)AEBDCSAS解：在△AEC和△ADB中∴△AEC≌△ADB（）∠A∠A公共角 例8:如图在△ABC中，AB＝AC，AD平分∠BAC，求证：　△ABD≌△ACD．证明:∵AD平分∠BAC，∴　∠BAD＝∠CAD．在△ABD与△ACD中，AB＝AC，(已知)∠BAD＝∠CAD，(已证)AD＝AD，(公共边)∴ABD≌△ACD（S.A.S.）．∵ 例9：小兰做了一个如图所示的风筝，其中∠EDH=∠FDH,ED=FD，将上述条件标注在图中，小明不用测量就能知道EH=FH吗？与同桌进行交流。EFDH解：在△EDH和△FDH中：ＥＤ＝ＦＤ（已知）∠EDH=∠FDH（已知）ＤＨ＝ＤＨ（公共边）∴△EDH≌△FDH（Ｓ.Ａ.Ｓ）∴EH=FH(全等三角形对应边相等） 例10：已知:如图,AB=DB,CB=EB,∠1＝∠2求证:∠A=∠D证明:∵∠1＝∠2(已知)∴∠1+∠DBC＝∠2+∠DBC(等式的性质)即∠ABC＝∠DBE在△ABC和△DBE中,AB＝DB(已知)∠ABC＝∠DBE(已证)CB＝EB(已知)∴△ABC≌△DBE(SAS)∴∠A=∠D(全等三角形的对应角相等)1A2CBDE 例题讲解，学会运用例　如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个不经过池塘可以直接到达点A和B的点C，连接AC并延长至D，使CD=CA，连接BC并延长至E，使CE=CB，连接ED，那么量出DE的长就是A，B的距离．为什么？ABCDE12 例题讲解，学会运用AC=DC（已知），∠1=∠2（对顶角相等），BC=EC（已知），证明：在△ABC和△DEC中，ABCDE12∴△ABC≌△DEC（SAS）．∴AB=DE（全等三角形的对应边相等）． １：如图，已知AB和CD相交与O,OA=OB,OC=OD.说明△OAD与△OBC全等的理由OA=OB(已知）∠1=∠2（对顶角相等）OD=OC（已知）∴△OAD≌△OBC(S.A.S)解：在△OAD和△OBC中CBADO21巩固练习 2.如图所示,根据题目条件，判断下面的三角形是否全等．（1）AC＝DF，　∠C＝∠F，BC＝EF；（2）BC＝BD，　∠ABC＝∠ABD．答案:(1)全等(2)全等巩固练习 如图，在△ABC和△ABD中，AB=AB，AC=AD，∠B=∠B，但△ABC和△ABD不全等．探索“SSA”能否识别两三角形全等问题3两边一角分别相等包括“两边夹角”和“两边及其中一边的对角”分别相等两种情况，前面已探索出“SAS”判定三角形全等的方法，那么由“SSA”的条件能判定两个三角形全等吗？ABCD 画△ABC和△DEF，使∠B=∠E=30°，AB=DE=5cm，AC=DF=3cm．观察所得的两个三角形是否全等？两边和其中一边的对角这三个条件无法唯一确定三角形的形状，所以不能保证两个三角形全等．因此，△ABC和△DEF不一定全等．探索“SSA”能否识别两三角形全等 （1）本节课学习了哪些主要内容？（2）我们是怎么探究出“SAS”判定方法的？用“SAS”判定三角形全等应注意什么问题？课堂小结 课本P100练习1、2、3注意：本次作业两题之间空3格。布置作业 SAS的探究：如果在△ABC和△A"B"C"中，AB=A"B"，∠B=∠B"，BC=B"C"，那么△ABC和△A"B"C"全等吗？问题：探究㈠：⑴、如果△ABC和△A"B"C"的位置关系如图①所示，则两个三角形全等吗？ABCC"(B")A"．A"C"思考：能否通过图形旋转试试？旋转演示：（图①） ⑵、如果△ABC和△A"B"C"的位置关系如图②所示，则两个三角形全等吗？探究㈡：C"A"B"B"A"C"BCA．（图②）能否通过图形的平移和旋转试试？思考：变换演示：变换演示： 第二章泻下剂概念:凡以泻下药为主组成，具有通导大便、荡涤实热，或攻逐水饮、寒积等作用，治疗里实证的方剂，称为泻下剂。立法依据:“其在下者，引而竭之”，“中满者，泻之于内”（《素问·阴阳应象大论》）。 适应范围：热结---便秘，伴壮热烦渴，苔黄脉实等寒结---便秘，伴畏寒肢冷，脘腹冷痛燥结---便秘，伴肠燥津亏等水结---水肿，腹胀，二便不利邪实正虚---便秘，兼正气虚弱症里实证 分类：寒下—里热积滞证。温下—里寒积滞证。润下—肠燥津亏便秘。逐水—水饮壅盛实证。攻补兼施—里实正虚便秘。 注意事项：1、表证未解，里已成实者，宜先解表、后治里或表里双解。2、年老体虚，孕妇、产妇，妇女经期，病后伤津亡血者，慎用或禁用。3、得效即止，慎勿过剂，免伤胃气。4、服药期间禁油腻及不宜消化食物。 大承气汤《伤寒论》功用：峻下热结主治：阳明腑实证（痞、满、燥、实）。热结旁流证。热厥、痉病、发狂属里热实证者。病证解析：痞满燥实—热邪与燥屎相结，腑气不通热结旁流—热结迫肠中津液从旁而下热厥--阳气受遏，不达四肢痉病--伤津劫液，筋脉失养发狂--热扰神明，心神浮越阳明腑实证腹气不通，阴液被耗实热积滞，内结肠胃 配伍意义：大黄--泻热通便，荡涤肠胃实君芒硝—咸寒软坚，泻热通便燥臣厚朴—下气除满满佐枳实--消痞破结痞使小承气汤：大黄、厚朴、枳实——轻下热结调胃承气汤：大黄、芒硝、甘草—缓下热结峻下热结 通因通用：反治法之一。针对某些实邪内结，郁滞在里，表现症象似通，而本质不通的病证采用通利的治法。 大黄牡丹汤功用：泻热破瘀，散结消肿。主治：肠痈初起，湿热瘀滞证。右下腹疼痛拒按，或右足曲而不伸，伸则痛甚，甚则局部肿痞，或时时发热，自汗恶寒，舌苔薄腻而黄，脉滑数。气血郁滞,正邪交争-发热,自汗，恶寒湿热郁蒸气血凝聚邪结肠中，腑气不通-右下腹疼痛拒按湿热内蕴-苔黄腻，脉滑数 配伍意义大黄-泻热逐瘀，荡涤肠中湿热瘀结之毒君丹皮-清热凉血,活血散瘀桃仁-破瘀活血芒硝-泻热导滞，软坚散结臣冬瓜仁-清肠利湿，排脓消痈佐使 大陷胸汤《伤寒论》功用:泻热逐水主治:水热互结的结胸证病症分析：心下满痛，甚则从心下至少腹硬满而痛不可近短气烦躁，大便秘结舌燥口渴—实热内结，津液耗伤日晡潮热—水热累及阳明脉沉紧，按之有力—里实热证之象水热互结，气机阻滞搏结于胸膈热邪与水饮结胸证 配伍意义：甘遂—攻逐水饮，泻热破结君大黄—苦寒峻下，荡涤邪热臣芒硝—苦寒软坚润燥佐泻热逐水 大黄附子汤《金匮要略》【功用】温里散寒，通便止痛【主治】寒积实证病证分析：便秘腹痛,胁下偏痛—寒实内积，腑气不通手足不温—阳气不达四末发热—阳气被郁舌苔白腻，脉弦紧—里实证之象互结于肠道寒邪与积滞寒积实证 配伍意义：附子—温里散寒君大黄—泻下通便,荡涤积滞臣细辛—温里散寒止痛，佐去性取用---大黄通便止痛温里散寒 温脾汤《备急千金要方》【功用】攻下冷积，温补脾阳【主治】阳虚寒积证。腹痛便秘，脐下绞结，绕脐不止，手足不温，苔白不渴，脉沉弦而迟。病证解析：便秘腹痛绕脐不止手足欠温，脉沉弦—脾阳不达四末肠间寒实冷积，腑气不通寒积中阻脾阳不足，冷积内结脾阳不足 配伍意义附子-温壮脾阳解散寒凝大黄-泻下通便以荡积滞芒硝-润肠软坚干姜-温中助阳臣人参-补脾益气,合附子温补阳气当归-养血和血佐甘草-调和诸药使配伍特点：温补脾阳配伍导下积滞药，以温补脾阳为主，泻下积滞为辅。君攻下冷积温补脾阳 温脾汤与大黄附子汤比较：同：均以附子配大黄为主体。异：大黄附子汤以大黄附子与辛温通散的细辛相伍，助附子温散寒凝以止痛，主治寒实积滞，正气不虚者。温脾汤则加干姜温中散寒，人参，甘草益气健脾。主治冷积内结，脾胃虚寒的虚中夹实证。 麻子仁丸《伤寒论》【功用】润肠泻热,行气通便【主治】胃肠燥热,脾约便秘证病证解析：脾不布津，但输膀胱—小便频数大便秘结-燥热伤津，肠失濡润苔微黄，脉细涩—燥热伤津之象脾约证肠失濡润脾津不足肠胃燥热 成无己：“约束津液不得四布，但输膀胱，致小便数而大便秘，故曰其脾为约。”《素问》：“饮入于胃，游溢精气，上输于脾，脾气散精，上归于肺，通调水道，下输膀胱，水精四布，五经并行，是脾主为胃行其津液者也。” 配伍意义：麻子仁---润肠通便君杏仁---上肃肺气，下润大肠白芍---养血敛阴，缓急止痛大黄---苦寒泄热，攻积通便枳实、厚朴-----行气破结除满蜂蜜---润燥滑肠，调和诸药使臣佐润肠泻热，行气通便小承气 配伍特点：本方即小承气汤加麻子仁、杏仁、白芍、蜂蜜而成，攻而不峻，润而不腻，有攻润相合之特点。 济川煎《景岳全书》【功用】温肾益精，润肠通便【主治】肾阳虚弱,精津不足证病证解析：大便秘结—肾虚精亏，肠失濡润小便清长—肾阳不足，气化无权腰膝酸软—肾虚精亏舌淡苔白，脉沉迟或沉涩—肾阳虚肾虚便秘肠失濡润肾虚精亏 配伍意义：肉苁蓉—温肾益精,暖腰润肠君当归—补血润燥,润肠通便牛膝—补肝肾、强筋骨腰膝枳壳—下气宽肠，有助通便泽泻—甘淡渗湿，祛除肾浊升麻—轻宣升阳，欲降先升配伍特点：补泻升降并用，寓通于补，寄降于升。臣佐使温肾益精，润肠通便升降同用 【功用】攻逐水饮【主治】悬饮，水肿。病证解析：咳唾胸胁引痛短气胸背掣痛不得息心下痞硬，干呕—水饮犯胃腹胀喘满二便不利头痛目眩—饮邪内阻，清阳不升全身水肿—水邪泛滥全身十枣汤《伤寒论》水饮停胸，气机不利水停肠腹，气机不利泛滥全身停于胸胁水邪壅盛 配伍意义：甘遂—善逐经隧之水湿君芫花--善消胸胁伏饮痰癖大戟--善泻脏腑之水湿臣大枣—培土制水，缓和诸药峻烈和毒性佐使用法：三药为散，大枣煎汤送服。小剂量开始（1～2克）；清晨空腹服用得快利后，糜粥自养攻逐水饮 黄龙汤《伤寒六书》【功用】攻下通便，补气养血【主治】阳明腑实，气血不足证病证解析：便秘，脘腹胀痛拒按；或热结旁流谵语神昏，肢厥，撮空神倦少气，脉虚--气血不足阳明腑实气血不足肠胃燥结邪热与燥屎内结 配伍意义：大黄、芒硝、枳实厚朴（大承气汤）人参、当归—益气养血臣桔梗—宣肺气，通肠腑生姜、大枣、甘草—补益脾胃调和诸药配伍特点：攻下扶正，邪正合治。攻下热结荡涤胃肠君佐使益气养血攻下通便'