最新4.2比较线段的长短课件PPT.ppt 84页

'进入夏天，少不了一个热字当头，电扇空调陆续登场，每逢此时，总会想起那一把蒲扇。蒲扇，是记忆中的农村，夏季经常用的一件物品。　　记忆中的故乡，每逢进入夏天，集市上最常见的便是蒲扇、凉席，不论男女老少，个个手持一把，忽闪忽闪个不停，嘴里叨叨着“怎么这么热”，于是三五成群，聚在大树下，或站着，或随即坐在石头上，手持那把扇子，边唠嗑边乘凉。孩子们却在周围跑跑跳跳，热得满头大汗，不时听到“强子，别跑了，快来我给你扇扇”。孩子们才不听这一套，跑个没完，直到累气喘吁吁，这才一跑一踮地围过了，这时母亲总是，好似生气的样子，边扇边训，“你看热的，跑什么？”此时这把蒲扇，是那么凉快，那么的温馨幸福，有母亲的味道！　　蒲扇是中国传统工艺品，在我国已有三千年多年的历史。取材于棕榈树，制作简单，方便携带，且蒲扇的表面光滑，因而，古人常会在上面作画。古有棕扇、葵扇、蒲扇、蕉扇诸名，实即今日的蒲扇，江浙称之为芭蕉扇。六七十年代，人们最常用的就是这种，似圆非圆，轻巧又便宜的蒲扇。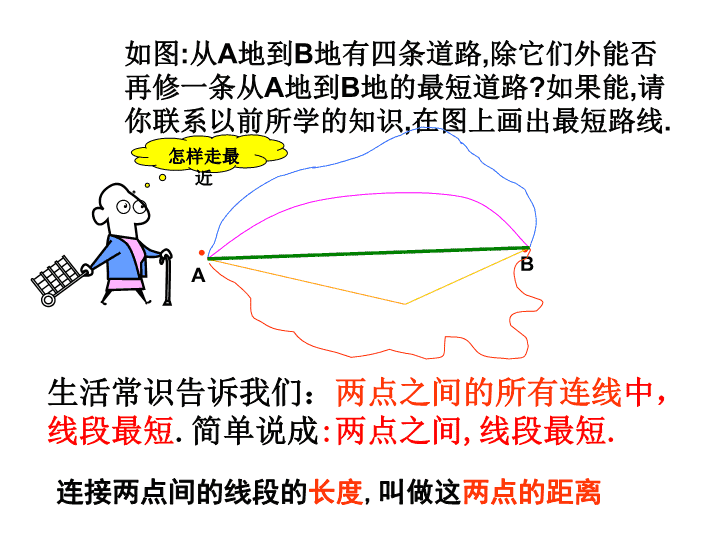　　蒲扇流传至今，我的记忆中，它跨越了半个世纪，也走过了我们的半个人生的轨迹，携带着特有的念想，一年年，一天天，流向长长的时间隧道，袅4.2比较线段的长短 如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.••AB怎样走最近连接两点间的线段的长度,叫做这两点的距离生活常识告诉我们：两点之间的所有连线中，线段最短.简单说成:两点之间,线段最短. 如图，从A地到B地最短的路线是（）A.A－C－G－E－BB.A－C－E－BC.A－D－G－E－BD.A－F－E－B 有条小河L，点A，B表示在河两岸的两个村庄，现在要建造一座小桥，请你找出造桥的位置，使得A，B两村的路程最短，并说明理由。LAB桥理由：两点之间,线段最短.答：连结AB交直线l于点P，点P就是所求作桥的位置P 草原上有4口油井，位于四边形ABCD的4个顶点，现在要建立一个维修站O，试问0建在何处，才能使它到4口油井的距离之和OA+OB+OC+OD为最小，说明理由.BDCA∴点O就是所求的位置。0答：连结AC、BD，交点O，理由是两点之间线段最短 （3）如图，A、B、C、D表示4个居民小区。现要建一个牛奶供应站，使它到4个小区的距离之和最小，你认为牛奶供应站应建在何处？标出牛奶供应站的位置，并说明理由。ACBDP∴点P就是所求的位置。理由是两点之间线段最短答：连结AC、BD，交点P， 如果线段AB=13cm，MA+MB=17cm，那么下面说法正确是（）A、点M在线段AB上B、点M在直线AB上C、点M在直线AB外D、点M在直线AB上，也可能在直线AB外D练习画图能力 已知线段AB=6cm，点P到A、B两点的距离相等，则PA+PB的长（）A、等于6cmB、小于6cmC、不小于6cmD、大于6cmC练习画图能力 第二课时 线段的和、差根据图形填空:（1）AB=+;D（2）AB=+=+=++;（3）CD=-=-,=--.ACCBADDBACCBACCDDBADACCBDBABACDB 线段的中点把一条线段分成两条相等的线段的点,叫做这条线段的中点。（如图点C是线段AB的中点）ABCAB＝4cm或写成∴AB=2AC=2BC∵C点是AB的中点∴AC＝CB＝21AB＝2cm ABC点B在线段AC上，以下关系式那些不能判断点B是线段AC的中点（）A.AB=BC=B.AC=2AB=2BCC.AC=AB+BCC 若AM=BM，则M为线段AB的中点。线段中点的条件：1、在已知线段上。2、把已知线段分成两条相等线段的点ABM错 如图AB＝8cm，点C是线段AB的中点，点D是线段CB的中点，那么线段AD是多长呢？解：ACBD∵C点是AB的中点∴AC＝CB＝21AB＝4cm∵D点是BC的中点∴CD＝21CB＝2cm∴AD＝AC+CD＝4+2＝6cm 在一条直线上顺次取A、B、C三点，使AB=5cm，BC=2cm,并且取线段AC的中点O，求线段OB的长。ABCO解：AC=AB+BC=5+2=7cm∴AO=OC=AC=3.5cm12OB=AB-AO（或OB=OC-BC=3.5-2=1.5cm）答：线段OB的长等于1.5cm.=5-3.5=1.5cm∵O点是AC的中点 4、直线l上有A、B、C三点，且AB=8cm，BC=5cm，求线段AC的长。lABClABC（1）当C点在线段AB的延长线上时（2）当C点在线段AB上时 分析：在“直线AB上画线段BC”这意味着要以B为所画线段的一个端点，另一个端点既可能在线段AB上，也可能在线段AB的延长线上。已知线段AB＝4cm，在直线上AB上画线段BC=3cm，求线段AC的长？ 已知线段AB＝8cm，点C是直线AB上一点，BC=2cm，求线段AC的长？ABABCC 已知线段AB=1cm,BC=3cm,则点A到点C距离为（）BA2cm或4cmB无法确定A,B，C不在一条直线上 若点B在直线AC上，AB=12，BC=7，则A、C两点的距离是_________5或19 设M地距离工厂5km，N地距M地10km，那么N地到工厂的距离为（）A5kmB15kmC5km或15kmD不能确定DM,N，工厂，不在一条直线上 已知线段AC=1，BC=3则线段AB的长度是（）A.4B.2C.2或4D.不能确定D变式：已知A、B、C是同一条直线上的三点，且线段AC=1，BC=3则线段AB的长度是____C 2或4 点C在数轴上，且AC：AB=1：5，求C对应的数__________分类讨论思想:BA-16或-6 5.5cm或2.5cm 在直线l上取A、B、C三点，使得AB=acm，BC=bcm，（a>b）如果O是线段AC的中点，则OB=_______cm。结论： 在直线l上顺次取A、B、C三点，使得AB=acm，BC=bcm，（a>b）如果O是线段AC的中点，则OB=_______cm。结论： MN如图所示，点C在线段AB上，点M,N分别是AC、BC的中点。CBA1、若AC=6,BC=4,求线段MN的长度.2、若线段AC=a,BC=b其他条件不变，求线段MN的长度的长度3、若将（1）小题中“点C在线段AB上”改为“点C在直线AB上”，（1）小题的结果会有变化吗？求线段MN的长度 例题分析如图，点C是线段AB上任意一点，点D是线段AC的中点，点E是线段BC的中点，则线段DE和线段AB有怎样的关系？说明理由...AB.C..DE解：∵点D是线段AC的中点∴DC=½AC∵点E是线段BC的中点∴CE=½BC∴DE=DC+CE=½AC+½BC=½（AC+BC）=½ABDE=½AB理由如下： 练一练：已知线段AB=6cm，延长线段AB至点C(如图)，使BC=AB，问：⑴线段AC的长为多少？⑵若点D为线段AC的中点，①求线段CD的长。②求BD的长。ABCD9cm4.5cm1.5cm 试比较线段AB、CD的长短。..ABCD..议一议(1)度量法用刻度尺量出线段AB长4cm，线段CD长4.5cm，所以线段AB比线段CD短。（记作AB＜CD或CD＞AB）(2)重合法将一线段“移动”，使其一端点与另一线段的一端点重合，两线段的另一端点均在同一射线上。 ABM点M把线段AB分成相等的两条线段AM与MB，我们把M点叫做线段AB的中点AM=BM=AB；AB=2AM=2BMABMNABM∵M、N为线段AB的三等分点∴AM=MN=NB=AB；AB=3AM=3MN=3NBNP∵M、N、P为线段AB的四等分点∴AN=MN=MP=PB=AB；AB=4AN=4MN=4NP=4PB AB（4）在铁丝框的A处有一只蚂蚁，在B处有一粒蜜糖，蚂蚁想吃到蜜糖，所走的最短路程是多少cm？4cm走进生活 AB4cm走进生活 AB4cm走进生活 ABC其余条件不变，把B处的蜜糖改成C处，又该如何？4cm走进生活 ABC那将“立方体的铁丝框”改成“立方体的纸盒”，上述两题结论又该如何呢？4cm走进生活 ACB那将“立方体的铁丝框”改成“立方体的纸盒”，上述两题结论又该如何呢？C”（C）C’（C）4cm走进生活 5.有关线段的计算问题(1)如图,A、B、C、D是直线l上顺次四点，且线段AC=5，BD=4，则线段AB-CD=_____.ABCDl(2)如图，AC=8cm，CB=6cm,如果O是线段AB的中点，求线段OC的长度。ABCO 第四章复习数学·课标版（BS）针对训练 第四章复习数学·课标版（BS） 第四章复习数学·课标版（BS） 第四章复习数学·课标版（BS） 第四章复习数学·课标版（BS） 如图所示,洋河酒厂有三个住宅区A、B、C各分别住有职工30人、15人、10人,且这三个区在酒家大道上(A、B、C)三点共线,已知AB=100米,BC=200米.为了方便职工上下班,该厂的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在_____区.ABC A，B，C是一条公路上的三个村庄，A，B间路程为100km，A，C间路程为40km，现在A，B之间建一个车站P，设P，C之间的路程为xkm.(1)用含x的代数式表示车站到三个村庄的路程之和；(2)若路程之和为102km，则车站应建在何处？(3)若要使车站到三个村庄的路程总和最小，问车站应建在何处？最小值是多少？ 如果线段AB=5cm，线段BC=4cm，那么点A、C两点之间的距离是_______。1cm或9cm 已知A、B两点之间的距离是10cm，C是线段AB上的任意一点，则AC中点与BC中点间的距离是（）A.3cmB.4cmC.5cmD.不能计算 小虫从点A爬到点C吃食物,请给小虫指明一条从点A到点C的最短路线.DCBA理由：两点之间，线段最短 如图所示,一只蚂蚁要从圆柱体A点沿表面尽可能地爬到B点,因为那里有它的食物,而它饿得快不行了,怎么爬行路线最短?··AB 如图,蚂蚁在圆锥底边的点A处,它想绕圆锥爬行一周后回到点A处,你能画出它爬行的最短路线吗?A MABCEFGH.思考题：如图是一个正方体，一只昆虫要从正方体的点A沿正方体的表面爬到G点，哪条线路最短？说明理由。GGFAMCBE.GCAFMBE. 第一节膝关节内侧副韧带损伤第二节髌骨张腱末端病第三节髌骨软骨软化症第四节半月板损伤第五节膝十字韧带损伤第六节髌骨脱位第九章膝部常见的损伤 一、概述1、解剖特点（1）是膝关节最重要的韧带，前股分为深浅两层，后股分为后上斜部和后下斜部；（2）膝内侧副韧带功能是：阻止膝关节的外翻或胫骨的外旋活动，保持关节的稳定性。2、发病情况：足球、排球、冰雪上项目等多见第一节膝关节内侧副韧带损伤 二、损伤机制1、当膝关节屈曲在150～160o时，小腿突然外展外旋或小腿固定，大腿急剧内收内旋时，皆可使膝内侧副韧带损伤。2、正常膝关节有10o的外翻，由于外方直接暴力作用于膝关节，使之外翻，亦可以产生内侧副韧带损伤。3、内侧副韧带损伤可分为：部分撕裂、完全撕裂和联合损伤。 三、临床症状及诊断：1、内侧副韧带损伤时，膝关节不能完全伸直，常保持在165～170o屈曲位，内侧有压痛、肿胀、皮下瘀血，膝关节伸直，小腿外展时，疼痛加重。2、联合损伤时，关节内有积血。3、韧带完全撕脱或断裂，可有关节的过度外翻活动及局部扪及凹陷。 四、治疗：1、无论那种损伤都要及早采取保守治疗，可收较好效果。2、急性期要微屈位（160°---170°）固定3、（1）推拿；（2）中药；（3）封闭。4、急性期后复查做其他治疗 一、概述1、发症情况：是运动损伤中多见的损伤，多发生于足球、排球运动中，多数患者无明显受伤史。2、本症历时较长，但预后良好。在整个发症期间要采取以运动为主，治疗为辅的治疗原则，充分调动患者主观能动性，无需停止训练进行治疗。第二节髌骨张腱末端病 二、损伤机制1、膝关节屈曲，要求股四头肌某部分承担较大负荷，使髌骨张腱相应区域的应力增大，易造成该区域的过度负荷。2、外力损伤（直接挫伤、捩伤），更能导致该病的形成。 三、临床表现：1、自觉髌骨边缘在半蹲，上下楼梯或跑跳发力时痛，关节酸软无力。2、髌骨指压痛：多见于下午4～８点钟处。3、压痛处触诊：髌骨边缘不整齐，有大小不等的颗粒增厚。4、特殊检查：单肢蹲起实验、抗阻伸膝试验、髌骨边缘试验。 四、治疗与预防：1、理疗；2、针灸、水针、封闭；3、预防：加强股四头肌的力量练习，训练前作好充分准备活动 一、概述1、髌骨软骨软化症是一种髌骨软骨面及与其相对的股骨髌面的关节软骨退行性病变。2、本病的发生与运动项目特点有明显关系。多见于篮球、排球，其它项目如足球、田径也有发生。3、本病的主要病理变化是软骨的退行性变，损伤后难于修复，所以对运动员的训练和成绩影响很大。第三节髌骨软骨软化症 二、损伤机制1、解剖生理：（1）髌骨前面粗糙，后面光滑为关节面（上2/3覆盖着关节软骨，下1/3没有关节软骨，全是骨性组织）。髌骨、腱区域周围没有腱鞘，而是由结缔组织构成的腱围。（2）髌骨的主要作用是：保护膝关节在半屈位的稳定性，防止膝异常的内收、外展以及前后错动 2、损伤机制：膝半蹲位，多次反复屈伸扭转，造成局部肌肉负担过重，破坏了膝关节各方的均衡拉力，迫使相连骨关节面不能按正常轨迹活动，久之使髌骨与股骨相互撞击和磨擦。如有局部外伤、负荷过度、硬地训练过多易激发该病。 三、临床表现：1、逐渐发病，早期自觉膝软、膝痛，只在大运动量后，以及半蹲、上下楼梯时明显，休息后消失，严重者各种活动均痛。2、髌骨边缘及周围软组织压痛，表明髌腱末端、关节囊继发损伤。3、髌骨边缘内侧压痛。4、压髌绷劲、髌骨分离、髌骨摩擦、半蹲检查阳性。四、治疗与预防：同前。 一、概述1、半月板是膝关节内的纤维软骨，位于股骨与胫骨关节软骨面之间。上面凹陷，符合股骨内外髁弧形关节面，下面平坦适应胫骨平台，起着调和关节形状及缓冲和保护关节面的作用，减少磨擦。第四节半月板损伤膝关节韧带及半月板结构 2、为适应关节运动和负重需要，膝关节伸直时，半月板向前滑动：屈曲时，半月板向后移行；旋转运动时，两侧半月板一个向前，一个向后。内侧半月板边缘与内侧副韧带相连，故其滑动度较少；外侧半月板外缘不与外侧副韧带相连，其间隔以腘肌腱，故滑动度较大。 3、半月板血供：（1）与半月板相关联的8条韧带。（2）关节囊中血管穿过半月板的外侧边缘而进入。（3）半月板血循环系由位于半月板上下表面滑膜层中的血管网和分布在半月板软骨内的血管组成。（4）半月板血管从外缘到内缘分为：血管区、少血管区、无血管区。血管区和少血管区损伤是可能愈合的。 二、损伤机制1、半月板损伤是较常见运动损伤之一。内侧半月板比外侧半月板更容易致伤。损伤程度可分为磨损、撕裂和破碎。损伤部位多位于半月板后角和体部。2、膝关节在屈伸过程中，小腿固定、大腿突然旋转动作时，由于人体重力作用线通过膝关节，产生研磨及撕裂的力量，容易伤及关节内未能迅速滑移的半月板。 三、临床表现1、受伤史肿痛关节积液2、上下楼梯痛3、绞锁与解锁：陈旧伤可反复出现。主诉膝关节突然有物“卡塞”，屈伸活动发生障碍，即绞锁；稍加抚摸或晃动后“卡塞”又自行解除。4、股四头肌萎缩。损伤后期股四头肌明显萎缩，关节软弱无力。 5、关节屈伸受限。与健侧比较，屈、伸范围均不及健侧。6、关节间隙压痛有异物感。固定压痛点，在80～120o内反复屈伸，指腹下可触及异物感（关节间隙处）。膝关节半月板压痛点检查法 7、特殊试验：（1）麦氏试验（摆动试验）；（2）Apley试验（研磨试验）。麦氏试验 四、治疗与预防1、急性期：以消肿散瘀为主。（1）固定外敷（2）中药（3）推拿。2、慢性期：以强筋健骨为主。可使用一些常用疗法及体疗。3、手术 第五节膝十字韧带损伤一概述又称交叉韧带，为关节内韧带分前、后交叉韧带，起止点略。后交叉韧带较粗和坚固很少损伤。膝无论伸直与屈曲交叉韧带均保持紧张。单独损伤较少见，多合并半月板与内侧副韧带损伤。前交叉韧带 二损伤机制膝半屈与伸直时，股骨下端前面与胫骨上端遭暴力打击，可引起单纯损伤。屈膝时突然旋转或突然极度屈膝会发生扭转伤与挤压伤。 三症状与诊断1受伤史，关节内撕裂感，疼痛剧烈，关节肿胀积血2抽屉试验阳性肿胀消退后要复查。四治疗与预防与内侧副韧带损伤相似。 一、概述由于股四头肌中的股直肌、股中间肌、股外侧肌的作用方向与髌韧带不在一条直线上，髌骨有向外脱出倾向，但因股内侧肌有向内上方牵引作用力而使髌骨维持在正常位置。第六节髌骨脱位 二、病因病理分为新鲜的外伤性与习惯性脱位。1、外伤性脱位：多由直接暴力引起。当外力直接作用于一侧或用力踢东西，突然用力伸膝，股四头肌强力收缩，可将其扩张部撕裂。以外脱位多见。2、习惯性脱位：多见于女性。单侧外侧脱位与外力作用和先天结构不正常有关。 三、症状与诊断1、新鲜的有外伤史、膝内侧或外侧疼痛、肿胀，损伤重的可有血肿、瘀斑。2、膝微屈、活动受限、前方凹陷，股骨下端内外侧可触及移位髌骨。3、X片。注意有无先天结构异常。 四、治疗1、手法复位：不需麻醉，患者平卧，立于患侧。一手握足踝，一手拇指按于髌骨外下方，余指托于腘窝下，使膝微屈状态作屈伸活动，在伸直同时，拇指向前方推髌骨,然后使患膝伸直。2、固定与练功用石膏托或绷带包扎于伸直位，4周左右。固定后患肢抬高，练习趾踝活动，解除固定后，锻炼膝屈伸功能，注意不能过早负重、用力伸膝下蹲。3、习惯性脱位可手术治疗'