最新专题九-线性赋范空间与巴拿赫空间g课件PPT.ppt 76页

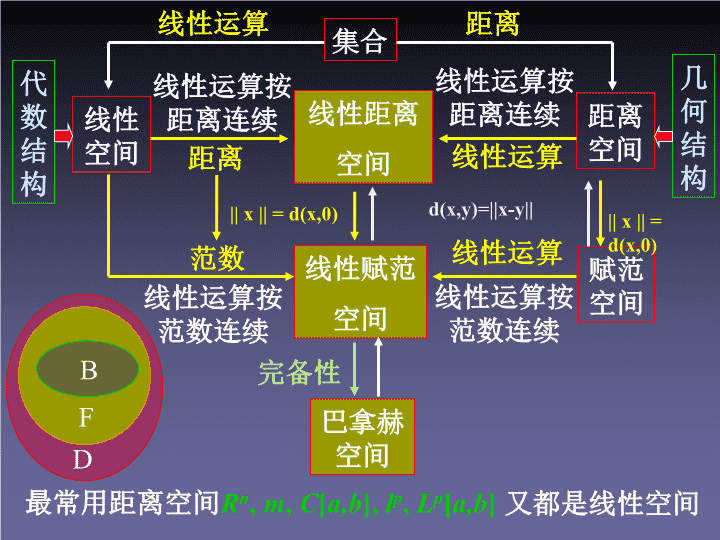
'专题九-线性赋范空间与巴拿赫空间g 线性赋范空间与巴拿赫空间专题九线性赋范空间与巴拿赫空间有限维线性赋范空间—线性代数研究对象无限维线性赋范空间—泛函分析研究对象 代数结构最常用距离空间Rn,m,C[a,b],lp,Lp[a,b]完备性范数线性赋范空间线性空间距离线性距离空间巴拿赫空间线性运算按范数连续线性运算按距离连续几何结构线性运算距离空间线性运算按范数连续赋范空间线性运算||x||=d(x,0)线性运算按距离连续||x||=d(x,0)又都是线性空间d(x,y)=||x-y||DFB集合距离线性运算 例3都是无限维线性空间（或）按通常的函数加法与数乘运算有：（或）（或）零元故都是线性空间证：逆元且满足1)—8)或（）（或） 定义2（线性子空间）设X是线性空间，MX，如果x,yM,,K,对于X中的加法和数乘运算，有x+yM,则称M是X的线性子空间。若MX，则称M为X的线性真子空间。定义3（由子集张成的线性子空间）设X是线性空间，MX。定义集合L：称L为由子集MX张成的线性子空间。注：spanM是包含M的最小线性子空间。即若L0也是包含M的线性子空间，必有2线性子空间 定义3(有限维线性空间的基和维数)1）e1,e2,…en线性无关;2）xX,x都能由e1,e2,…,en线性表示，即1,2,…,nR,使x=1x1+2x2+…nxn则称e1,e2,…,en为X的一个基底,x1,x2,…,xn为向量关于基底e1,e2,…,en的坐标。称n维线性空间X的维数，而称X为n维线性空间。并记dimX=n。注：1)如果X={},则称X是零维线性空间,这时X没有基。3线性空间的基与维数设X是线性空间,e1,e2,…,enX,如果2)xX,它关于基底e1,e2,…,en的坐标是唯一的。3)任何有限维线性空间的基底都不唯一。n维线性空间中的任何n个线性无关的向量都可以作为X的基底。 定义4(无限维线性空间的基)1）e1,e2,…,en,…线性无关;2）xX,x都能由e1,e2,…,en,…线性表示，即1,2,…,n,…R,使x=1e1+2e2+…nen+…则称e1,e2,…,en,…为X的一个基底,x1,x2,…,xn,…为向量关于基底e1,e2,…,en,…的坐标。也称X为无限维线性空间。设X是线性空间,e1,e2,…,en,…X,如果注：1）任何线性空间X{}都有基。2）对于无限维线性空间X，如果e1,e2,…,en,…X线性无关，且X=span{e1,e2,…,en,…},则称e1,e2,…en,…为X的Hamel基。 例4n为欧氏空间Rn是n维线性空间。例5C[a,b]是一个无限维线性空间。1）e1=（1,0,…,0),e2=(0,1,…,0),…,en=(0,0,…,1)称为Rn的标准基（或单位坐标基）x=(x1,x2,…,xn)Rn在基e1,e2,…,en下的坐标位x1,x2,…,xn。是Rn的另一组基。函数系1,t,t2,…,tn,…是C[a,b]的一个基底。证：如果C[a,b]是有限维线性空间，维数为n,则1,t,t2,…tnC[a,b]线性相关（任何n+1个n维向量都线性相关。这与1,t,t2,…tn对任何n都线性无关矛盾。 例6[a,b]区间上多项式函数的全体构成的集合P[a,b]按照通常的加法和数乘是一个无限维线性空间。证：显然P[a,b]是线性空间。对n,1,t,t2,…tnP[a,b]线性无关，故P[a,b]是无限维空间。x=x(t)P[a,b],都能有1,t,t2,…tn,…线性表示，故1,t,t2,…,tn,…是P[a,b]的一个基底。函数系1,t,t2,…,tn,…是P[a,b]的一个基底。注：函数空间P[a,b]C[a,b]Lp[a,b]按照通常的函数运算都是无限维线性空间，1,t,t2,…,tn,…是他们的一个公共基底。 例7序列空间S（有限个分量不为零数列全体）、有界数列空间m、p幂可和数列空间lp按照通常的数列加法和数乘运算都是无限维线性空间。他们的标准基底都是：e1=(1,0,…,0,0,0,…),e2=(0,1,…,0,0,0,…),…,en=(0,0,…,0,1,0,..)证：设S={x=(1,2,…,n,…)|i0,i为有限数}S是一线性空间(按通常数列加法和数乘）如果S是有限维线性空间，xi=(i1,i2,…,iN,0,0,…)(i=1,2,…,m)使S的一个基底则x=(1,2,…,N,0,0,…)S，有x=1x1+2x2+…+mxm即x可由x1,x2,…xm线性表示。但eN+1=(0,0,…,0,1,0,…)S种地N+1位分量0故eN+1不可能由x1x2,…,xm线性表示。矛盾。故S是无限维线性空间Smlp,因此m,lp也都是无限维线性空间。 4线性同构定义4（线性同构）设X和Y是两个线性空间（同为实的或复的）。如果一个映射：XY，使得x1,x2X及R(或C)，成立注：1）两个同构的线性空间可以看作是同一的。(x1+x2)=(x1)+(x2)，(x1)=(x1)则称X与Y是线性同构的，也称是从X到Y的线性同构映射。2）线性无关的向量组线性无关的向量组线性同构3）同构映射的逆映射仍是同构映射 注：1）线性空间的任意线性子空间都是凸集。5凸集的概念定义6（凸集）设X为线性空间，AX。如果对x,yA,01，有x+(1-)yA，则称A为X中的凸集.2）任意个凸集的交仍是凸集。3）如果BX，且BAi,Ai(iI)为X的一族凸集，则定义5（凸组合）（1）x+(1-)y（01）称为为x与y的凸组合。（2）1x1+2x2+…+nxn（0i1,1+2+…+n=1）称为为x1,x2,…,xn的凸组合。为包含B的最小凸集，成为B的凸包。 1范数与线性赋范空间二、线性赋范空间与巴拿赫空间定义72由范数诱导的距离定义8范数公理 注：——由线性度量空间构造范数使之成为赋范线性空间的方法 例8数列空间1）定义1(x,y)满足距离公理，是S上的距离函数故S是距离空间2）S按照通常数列的加法和数乘运算是线性空间3）但距离函数1(x,y)不是由范数诱导的距离：事实上，当||1时， 3常见空间的范数与距离对照表(1)Rn(2)m(3)lp(4)C[a,b](5)Lp[a,b] 例如：4巴拿赫（Banach)空间定义9完备的线性赋范空间称为巴拿赫空间。因此Rn是Banach空间。 定理1设X是线性赋范空间，{xn}、{yn}X,x,yX,{n}R,R如果n,xnx,yny,则有xnx,nxx,xn+ynx+y证n|n-|0xnx||xn-x||0yny||yn-y||0||xn-x||=||||xn-x||0xnx||nx-x||=|n-|||x||0nxx||(xn+yn)-(x+y)||=||(xn-x)+(yn-y)||||xn-x||+||yn-y||0xn+ynx+y5线性赋范空间中的极限理论定义10（极限）设X是线性赋范空间，{xn}X,xX。线性赋范空间中线性运算对范数的连续性 定理2设X是线性赋范空间，{xn}X,xX.1)如果xnx,则{||xn||}有界（范数列的有界性）；证1)xnx||xn-x||0||xn||||xn-x||+||x||||x||{||xn||}有界如果xnx,则||xn||||x||(范数的连续性，即||x||是x的连续函数）；2)一方面，||xn||-||x||||xn-x||另一方面，||xn||-||x||=||xn||-||x-xn+xn||||xn||-(||x-xn||+||xn||)=-||xn-x||因此|||xn||-||x|||||xn-x||xnx||xn-x||0|||xn||-||x|||0||xn||||x|| 定理3设X是线性赋范空间，d是由范数诱导的距离，则对x，y,z0X有.1)平移不变性：d(x+z0,y+z0)=d(x,y)证1)d(x+z0,y+z0)=||(x+z0)-(y+z0)||=||x-y||=d(x,y)2)绝对齐次性：d(x,y)=||d(x,y)2)d(x,y)=||x-y||=||||x-y||=||d(x,y) 设{xn}是线性赋范空间X中的点列，表达式5线性赋范空间中的无穷级数称为X中的无穷级数称为级数的部分和。如果存在sX,使得||sn-s||0(n),则称级数收敛于s，s称为级数的和，记为 如果数项级数收敛，则称级数绝对收敛；当X是巴拿赫空间时，若级数绝对收敛则级数一定收敛。6线性赋范空间中的完备化定义5（线性等距同构）设（X1，1）和（X2，2）是同一数域上的两个线性赋范空间。如果存在一一映射T：X1X2，满足：T(x+y)=T(x)+T(y)，则称X1与X2是线性等距同构的，也称T是从X1到X2的线性等距同构映射。（1）线性：x,yX及，，成立（2）等距：xX，成立Tx2=x1 注：两个同构的线性空间可以看作是同一的。定理4（完备化定理）设（X，）是一线性赋范空间，则必存在唯一的巴拿赫空间Y，使X与Y的一个稠密子空间Y1线性等距同构。例如，C[a,b]按范数不完备，其完备化空间是L2[a,b]. 6线性赋范空间的基本性质定理3线性赋范空间X中的球（开或闭）是凸集。证 有限维线性赋范空间是研究无限维空间的有力工具。三、有限维线性赋范空间的特殊性质1n维线性赋范空间的模型（反映了与欧氏空间Rn的关系是Rn上的连续函数。定理5设X是n维实线性赋范空间，xX在基底{e1,e2,…,en}下的坐标为(1,2,…,n),令x=(1,2,…,n)，则~证有限维线性赋范空间具有特殊性质(来自它与欧氏空间的相似性) 有限维线性赋范空间是研究无限维空间的有力工具。三、有限维线性赋范空间的特殊性质有限维线性赋范空间具有特殊性质(来自它与欧氏空间的相似性) 1n维线性赋范空间的模型（反映了与欧氏空间Rn的关系）定理1n维实线性赋范空间X与n维欧氏空间Rn（在某种范数下）是线性等距同构的。证设{e1,e2,…,en}是X的一个基底，(1,2,…,n)Rn,xX，也使得X与Rn之间存在着一一对应关系T：xX，(1,2,…,n)Rn,使得 1）T是线性同构映射：2）T关于X与Rn的某种范数是等距同构映射： 在Rn中定义实值函数：故是Rn中的范数，记作：则 注：任何n维线性赋范空间的模型都可以看作Rn，从而任何有限维线性赋范空间都是完备的。2范数的等价性定义2（等价范数）设||·||1，||·||2是同一线性空间X中的两个不同的范数。如果当||·||10时有||·||20，则称||·||1比||·||2更强；如果||·||1比||·||2更强，切||·||2比||·||1更强，则称||·||1与||·||2等价。定理2（范数等价的充要条件）线性空间X中的两个范数||·||1与||·||2等价的充要条件是：xX，存在两个正数a，b，使得 3有限维线性赋范空间的特殊性质定理3设X是n维实线性赋范空间，{e1,e2,…,en}是X的一个基底，则a,b>0,使对xX,有证一方面 另一方面是Rn中的范数，因而在Rn上非负连续在Rn中的有界闭集（单位球面）上有最小值a 注：定理中， 定理4（范数等价性）设X是有限维线性赋范空间，则X上的任何范数都等价。证设||·||1，||·||2是X上的任意两个范数，则根据定理3，使||·||1与||·||2等价注：定理4表明，有限维线性赋范空间X上的任何范数的收敛性相同，因而在讨论极限时可以任意选取范数。 推论1任意有限维线性赋范空间都是Banach空间，从而任意有限维线性赋范空间的子空间都是闭子空间。证设X是n维线性赋范空间，{xk}X是柯西序列，{e1,e2,…,en}是X的一个基底，映射T:XRn.是柯西列收敛于某X完备 推论2n维实线性赋范空间X与n维欧氏空间Rn是拓扑同胚的。证设{e1,e2,…,en}是X的一个基底，作一一映射T：则T是拓扑同胚映射。事实上，由定理3有T是连续映射T-1是连续映射 2）T是拓扑同胚映射（即T与T-1都是连续映射）：X是n为线性赋范空间，M1>0,M2>0,使T是连续映射T-1是连续映射T是拓扑同胚映射注：在线性同构和拓扑同胚意义下，任意n维线性赋范空间都与Rn“等同”。 推论2任意有限维线性赋范空间都是Banach空间，从而任意有限维线性赋范空间的字空间都是闭子空间。证设X是n维线性赋范空间，{xk}X是柯西序列，{e1,e2,…,en}是X的一个基底，映射T:XRn.是柯西列收敛于某X完备X是Banach空间X的任意子空间完备，是闭子空间。推论1 证闭集LX,LX.x1XL,令Riesz引理是泛函分析中重要定理---在区别有限维与无限维线性赋范空间的某些特征方面起关键作用。定理4（黎斯F·Riesz引理）设X是线性赋范空间，LX是真闭子集（子空间），则对(0<<1),x0X,使||x0||=1,且对xL,有x’L,使下确界定义令X对线性运算封闭对xL,有||x’-x1||x+x’LLX对线性运算封闭x’x1x0xd 定理5X是有限维线性赋范空间X中的任意有界闭集都是（列）紧集。（有限维空间的特征性定理）证必要性设X是n维线性赋范空间，T:XRn是线性等距同构和拓扑同胚映射。T(A)={y|y=Tx,xA}Rn是有界闭集{xn}A{Txn}T(A)T(A)是列紧集{Txnk}{Txn}T(A),使TxnkTx0T(A)Rn中有界闭集是列紧集A为列紧集A为紧集xnkx0AT拓扑同胚T与T-1均连续AX为有界闭集拓扑同胚映射性质 充分性设X中任意有界闭集是列紧集取单位球面B={x|||x||=1,xX}XB是列紧集若X是无限维线性赋范空间，x1S,令B1=span{x1}B1X,B1X是一维闭子空间x2B,||x2||=1,使（Riesz引理）B2X,B2X是二维闭子空间x3B,||x3||=1,使（Riesz引理）令B2=span{x1,x2}{xi}B,||xi||=1,使{xi}无收敛子序列。这与B是紧集矛盾。X是有限维线性赋范空间。 推论3有限维线性赋范空间中的单位球面是（列）紧集。推论4在有限维线性赋范空间中，紧集有界闭集。推论5在无限维线性赋范空间中，单位球面不是紧集，紧集与有界闭集不等价。注：单位球面是（列）紧集是有限维线性赋范空间独有的特性。如果某线性赋范空间中的单位球面是紧集，那么该线性赋范空间一定是有限维空间。 2有限维线性赋范空间与无限维线性赋范空间本质区别定理7X是有限维线性赋范空间X中的任意有界闭集都是（列）紧集。（有限维空间的特征性定理）证必要性设X是n维线性赋范空间，T:XRn是线性同构和同胚映射。AX为有界闭集T(A)={y|y=tx,xA}R是有界闭集{xn}A{Txn}T(A)T(A)是列紧集拓扑同胚映射性质{Txnk}{Txn}T(A),使TxnkTx0T(A)Rn中有界闭集是列紧集A为列紧集A为紧集xnkx0TAT拓扑同胚T与T-1均连续充分性设X中任意有界闭集是列紧集取单位球面B={x|||x||=1,xX}XB是列紧集若X是无限维线性赋范空间，x1S,令B1=span{x1}B1X,B1X是一维闭子空间x2B,||x2||=1,使Riesz引理x2x3x1BB1Xx4 B2X,B2X是二维闭子空间x3B,||x3||=1,使Riesz引理令B2=span{x1,x2}{xi}B,||xi||=1,使{xi}无收敛子序列。这与B是紧集矛盾。X是有限维线性赋范空间。推论3有限维线性赋范空间中的单位球面是（列）紧集。推论4在有限维线性赋范空间中，紧集有界闭集。推论5在无限维线性赋范空间中，单位球面不是紧集，紧集与有界闭集不等价。注：单位球面是（列）紧集是有限维线性赋范空间独有的特性。如果某线性赋范空间中的单位球面是紧集，那么该线性赋范空间一定是有限维空间。 慢性支气管炎、阻塞性肺气肿疾病的防治及护理 一、概述二、病因和发病机制三、临床表现四、有关检查五、诊断要点六、治疗要点七、护理诊断／问题八、护理措施九、健康教育 一、概述慢性支气管炎简称慢支，是指气管支气管粘膜及其周围组织的慢性非特异性炎症。临床上以咳嗽、咳痰或伴有喘息及反复发作的慢性过程为特征。病情若缓慢进展，常并发阻塞性肺气肿，甚至肺动脉高压、肺原性心脏病。它是一种常见病，尤以老年人多见。 肺气肿是指终末支气管远端的气道弹性减退、气腔异常扩大，或同时伴有气道壁破坏的病理状态。慢支引起的慢性阻塞性肺气肿，是由于慢性炎症蔓延至气道远端，累及细支气管管壁及周围组织，造成气体排出受阻，使肺泡过度膨胀和肺泡壁弹性减弱或破坏融合成肺大泡所致。病人在咳嗽、咳痰的基础上出现逐渐加重的呼吸困难，可并发慢性肺源性心脏病和Ⅱ型呼吸衰竭。 慢性支气管炎和慢性阻塞性肺气肿都有气流受阻的现象，把具有气流受阻特征的一类疾病称为慢性阻塞性肺疾病（简称COPD）。 二、病因和发病机制（一）病因1.吸烟纸烟中含有焦油、尼古丁等，可使支气管痉挛，呼吸道上皮细胞纤毛运动受抑制，纤毛脱落，而易致感染。2.感染病毒感染与细菌感染，常见病毒为鼻病毒、流感病毒、腺病毒及呼吸道合胞病毒；常见细菌为肺炎球菌和流感嗜血杆菌等。3.大气污染包括二氧化硫、二氧化氮、氯及臭氧等的慢性刺激。4.气候冷空气刺激、气候突然变化，使呼吸道黏膜防御能力减弱，易继发感染。5.遗传因素已证明抗胰蛋白酶缺乏，与肺气肿的发生有密切关系。 （二）发病机制发病机制尚未完全阐明，可能与多种因素共同作用有关。在病因的作用下，支气管壁可有各种炎性细胞浸润，炎性物质的释放，如前列腺素、白三烯、组胺、淋巴因子及溶酶体成分，导致黏膜下腺体增生、分泌增加及黏液纤毛运动障碍和气道清除能力削弱，出现黏膜充血水肿、增厚，加剧了气道阻塞，易于感染及发病。慢性炎症使巨噬细胞和中性粒细胞释放弹性蛋白酶、水解肺泡壁内的弹性蛋白，使肺泡壁破坏失去弹性，肺泡腔扩大，同时毛细血管损伤使组织营养障碍而发展成肺气肿。在发生气流阻塞时，小气道病变是主要原因。 三、临床表现（一）慢性支气管炎的症状、体征慢支症状表现为"咳"、"痰"、"喘"、"炎"四症。早期咳嗽较轻微，只在气候寒冷或突变时发生，重者则四季均咳。一般晨间咳嗽较重，痰液多为白色黏液泡沫状，当发生感染时，痰量增多，尤以体位变动或清晨起床时痰量较多，可有脓性及黏液脓性痰，偶可带血。喘息型慢支有支气管痉挛，可有喘息。早期可无异常体征，长期患病可在背部及肺底部出现散在的干、湿啰音，急性发作时，啰音可增多，喘息型慢支发作时，可闻哮鸣音。 （二）阻塞性肺气肿的症状、体征慢性支气管炎反复急性发作不断加重，形成阻塞性肺气肿。除慢支症状外，主要症状为逐渐加重的呼吸困难，初期可在劳累后出现，随病情发展，甚至在静息时也感到呼吸困难。当慢支急性发作时，进一步加重通气功能障碍，使胸闷气急加重。典型肺气肿的体征为：桶状胸，胸部呼吸运动减弱；语颤减弱；叩诊过清音；听诊呼吸减音弱。 四、有关检查（一）血液检查继发细菌感染时，白细胞总数及中性粒细胞比例增多。（二）x线检查可见肺纹理增多及紊乱，肺气肿时，两肺透亮度增加，肋间隙增宽。（三）肺功能检查在慢支早期可正常。COPD早期可有小气道功能异常，以后可出现第1秒用力呼气量占用力肺活量比值减少；慢支并发阻塞性肺气肿时，残气容积增加，残气容积占肺总量百分比增加。 五、诊断要点1.慢性支气管炎：以咳嗽、咳痰为主要症状或伴有喘息，每年发病持续3个月，持续2年或以上，能排除其他疾患引起的咳嗽咳痰。临床上可分为两型。单纯型：主要具有咳嗽、咳痰两项症状；喘息型除有咳嗽咳痰外，伴有喘息，并有哮鸣音。2.阻塞肺气肿：根据慢性支气管炎发病史，肺气肿的症状及体征，X线胸片及肺功能检查一般可以做出诊断。 六、治疗要点1.戒烟，控制各种诱发因素。由于慢支及肺气肿为慢性病，应帮助患者了解疾病，增加其治疗疾病的信心。2.对慢支患者在急性发作期要控制感染，祛痰止咳，解痉平喘。用药：（1）抗生素：应根据致病菌的性质及药物敏感程度选择。较轻患者，多选择口服及肌注抗生素，而对于较重患者，多选用静脉注射抗菌谱较广的药物。常用的药物包括青霉素类、头孢菌素类、大环内酯类、氨基糖苷类和喹诺酮类。（2）支气管扩张剂：茶碱类如氨茶碱；受体兴奋剂如沙丁胺醇；抗胆碱能药物如异丙阿托品等，可缓解支气管痉挛的症状。（3）祛痰止咳：祛痰药物如乙酰半胱氨酸、溴己新等，也可使用中药化痰。对老人、体弱者及痰多者，不应使用强镇咳剂，如可待因等。（4）雾化吸入：痰液黏稠者可采用雾化吸入，雾化液中可加入抗生素及痰液稀释剂。 七、护理诊断／问题1.清理呼吸道无效：与痰液黏稠，支气管痉挛等有关。2.低效性呼吸型态：与支气管阻塞、呼吸阻力增加有关。3.活动无耐力：与低氧血症、营养不良等有关。4.气体交换受损：与COPD继发感染有关。5.焦虑、个人应对无效：与呼吸困难迁延、家庭支持不足或缺乏有关信息有关。6.潜在并发症：自发性气胸、呼吸衰竭。 八、护理措施（一）遵医嘱给予抗炎治疗，有效地控制呼吸道感染鼓励病人咳嗽，指导病人正确咳嗽，促进排痰。痰量较多不易咳出时，按医嘱使用祛痰剂或给予超声雾化吸入。 （二）改善呼吸状况对阻塞性肺气肿患者的治疗主要为改善呼吸功能。1.合理用氧：低氧血症者按医嘱实施合理氧疗，可鼻导管持续（或吸氧时间每天15小时以上）低流量吸氧，一般氧流量为1~2升，浓度为25%~29%，以提高氧分压，并避免吸入氧浓度过高引起二氧化碳潴留COPD病人因长期二氧化碳潴留，呼吸中枢对二氧化碳已不敏感，主要通过缺氧刺激外周化学感受器反射性兴奋呼吸中枢，吸入较高浓度的氧气可削弱缺氧的刺激，使通气抑制，加重二氧化碳潴留，严重时可导致呼吸停止。。 向病人说明氧疗的重要性，嘱其不要擅自停止吸氧或变动氧流量，特别是睡眠时氧疗不可间歇，以防熟睡时呼吸中枢兴奋性减弱或上呼吸道阻塞而加重低氧血症。 2.呼吸训练：腹式呼气和缩唇呼吸训练腹式呼吸训练：肺气肿患者常呈浅速呼吸，呼吸效率低，让患者作深而慢的腹式呼吸，通过腹肌的主动舒张与收缩加强腹肌训练，可使呼吸阻力减低，肺泡通气量增加，提高呼吸效率。 训练方法如下：①体位：开始训练时以半卧位，膝半屈曲最适宜。立位时上半身略向前倾，可使腹肌放松，舒缩自如，全身肌肉特别是辅助呼吸肌尽量放松，情绪安定，平静呼吸。 ②呼吸训练：用鼻吸气，经口呼气，呼吸要缓慢均匀，切勿用力呼气，吸气时腹肌放松，腹部鼓起，呼气时腹肌收缩，腹部下陷。开始训练时，患者可将一手放在腹部，一手放在前胸，以感知胸腹起伏，呼吸时应使胸廓保持最小的活动度，呼与吸时间比例为2～3：1，每分钟l0次左右，练习数次后可稍事休息，两手交换位置后继续进行训练。每日训l练两次，每次l0～15分钟，熟练后可增加训练次数和时间，并可在各种体位时随时进行练习。 缩唇呼气训练：：肺气肿患者因肺泡弹性回缩力减低，小气道阻力增高，呼气时小气道提早闭合致使气体滞留在肺泡内，如在呼气时将口唇缩成吹笛子状，气体经缩窄的口唇缓慢呼出称缩唇呼气。其作用是提高支气管内压，防止呼气时小气道过早陷闭，以利肺泡气排出。总之，患者掌握腹式呼吸，并将缩唇呼气融人其中，便能有效增加呼吸运动的力量和效率，调动通气的潜能。 有效咳嗽咳痰的方法及指导深呼吸和有效咳嗽.咳痰:适用于神志清醒能咳嗽的病人.其方法为：病人取坐位，双脚着地，身体稍前倾，双手环抱一枕头，有助于膈肌上升，进行数次深而缓慢的呼吸，于深吸气末屏气，然后缩唇，缓慢地通过口腔尽可能地呼气；再深吸气后屏气3~5秒，从胸腔进行2~3次短促有力的咳嗽，张口咳出痰液，咳嗽时收缩腹肌，或用自己的手按压上腹部，帮助咳嗽。 胸部扣击与胸壁震荡：适用于久病体弱，长期卧床，排痰无力者，禁用于未经引流的气胸，肋骨骨折，咯血及肺水肿等病人。操作时要监测生命体征和肺部诊，明确病变部位，宜用单层薄布保护胸廓部位，避免直接扣击引起皮肤发红，避免过厚覆盖物降低扣击时的震荡效果，扣击时避开乳房，心脏和骨突部位，解开拉链，纽扣等硬物。扣击时病人取侧卧位，扣击时右手的手指指腹并拢，使掌侧呈杯状，以手腕力量，由肺底自下而上，由外向内迅速而有节律的扣击胸壁，震动呼吸道，每一肺叶扣击1~3分钟，120~180次/分。操作时力量适中，以病人不感到疼痛为宜，每次扣击时间5~15分钟为宜，应安排在餐后2小时至餐前30分钟完成。 湿化和雾化疗法：其目的是湿化呼吸道，稀释痰液，适用于痰液粘稠而不易咳出者。常用湿化剂有蒸馏水，生理盐水，低渗盐水。临床上常在湿化剂中加入药物（如痰溶解剂，支气管舒张剂，激素等）以雾化的方式吸入，以达到祛痰，止咳，消炎，平喘的作用。 机械吸痰：适用于无力咳出黏稠痰液，意识不清或排痰困难者。可经病人的口，鼻腔，气管插管或气管切开处进行负压吸痰。每次吸引时间不超过15秒，两次抽吸时间大于3分钟。并在吸痰前，中，后适当提高吸入氧的浓度，避免吸痰引起低氧血症。 饮食：要给予高热量、高蛋白质、高维生素饮食，少吃产气食品，防止产气影响膈肌运动。应重视营养摄人，改善营养状态，提高机体的免疫力。 全身性运动：全身运动锻炼结合呼吸锻炼能有效挖掘呼吸功能潜力，可进行步行、骑自行车、气功、太极拳、家庭劳动等，锻炼方式、锻炼时速度、距离，根据病人身体状况决定。 心理护理：由于长期呼吸困难，病人容易丧失信心，多有焦虑、抑郁等心理障碍，护士应聆听病人的叙述，做好病人与家属及单位间的沟通，疏导其心理压力，必要时请心理医生协助诊治。 九、健康教育1.戒烟，使病人了解吸烟的危害，改善生活环境。2.增强体质，防止急性呼吸道感染，进行耐寒锻炼。重视缓解期营养摄人，改善营养状况。3.坚持全身运动和呼吸训练，进行适宜的全身活动，指导病人制定合理的运动计划。4.家庭氧疗的指导。长期氧疗可以改善COPD病人的预后，提高其生活质量，给有此医嘱的病人提供有关家庭氧疗的咨询与帮助。5.坚持进行腹式呼吸及缩唇呼气训练。6.关注病人的心理问题，居家病人常有明显的孤独感，抑郁的发生率较高。因此，家人及朋友除在提供身体方面的关怀外，在心理上应更多给予关注与帮助。 谢谢您'