最新电路第6章(修改)课件PPT.ppt 40页

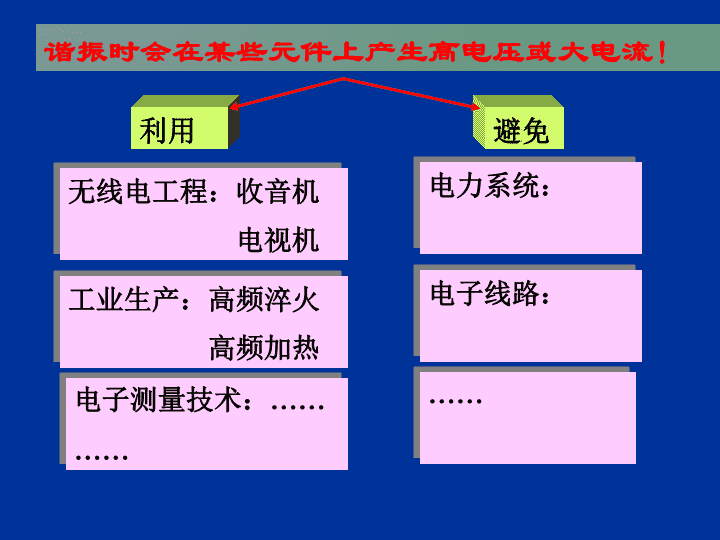
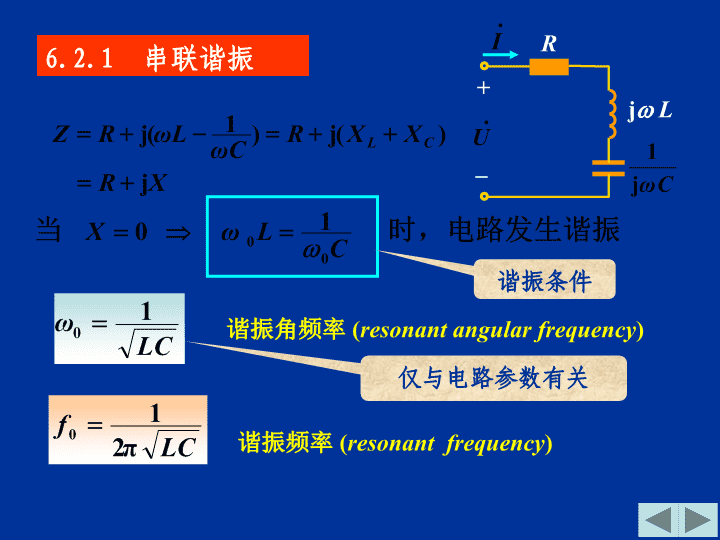
'电路第6章(修改) 利用避免无线电工程：收音机电视机电子测量技术：…………工业生产：高频淬火高频加热电力系统：谐振时会在某些元件上产生高电压或大电流！电子线路：…… RjL+_6.2.1串联谐振谐振角频率(resonantangularfrequency)谐振频率(resonantfrequency)谐振条件仅与电路参数有关 例某收音机L=0.3mH，R=10，为收到中央电台560kHz信号，求（1）调谐电容C值；（2）如输入电压为1.5V求谐振电流和此时的电容电压。+_LCRu解 (3)谐振时的功率P=UIcos＝UI＝RI02=U2/R，电源向电路输送电阻消耗的功率，电阻功率达最大。电源不向电路输送无功。电感中的无功与电容中的无功大小相等，互相补偿，彼此进行能量交换。+_PQLCR 例一接收器的电路参数为：L=250mH,R=20W,C=150pF(调好),U1=U2=U3=10mV,w0=5.5106rad/s,f0=820kHz.+_+_+LCRu1u2u3_f(kHz)北京台中央台北京经济台jL8206401026jX-j1290–j1660-j10340–j660-j577j1290j1000j1611I0=0.5I1=0.0152I2=0.0173I=U/|Z|(mA) I0=0.5I1=0.0152I2=0.0173I=U/|Z|(mA)小得多∴收到北京台820kHz的节目。8206401200I(f)f(kHz)0 例一接收器的电路参数为：U=10Vw=5103rad/s,调C使电路中的电流最大，Imax=200mA，测得电容电压为600V，求R、L、C及Q+_LCRuV解 1.G、C、L并联电路对偶：RLC串联GCL并联6.2.2并联电路的谐振+_GCL谐振角频率 RLC串联GCL并联|Z|ww0OR0OI()U/R0OU()IS/G|Y|ww0OG RLC串联GCL并联电压谐振电流谐振UL(w0)=UC(w0)=QUIL(w0)=IC(w0)=QIS 2.电感线圈与电容器的并联谐振实际的电感线圈总是存在电阻，因此当电感线圈与电容器并联时，电路如图：谐振时B=0，即CLR（1）谐振条件 此电路发生谐振是有条件的，在电路参数一定时，满足一般线圈电阻R<<L，则等效导纳为：等效电路谐振角频率GeCL (b)电流一定时，总电压达最大值：(c)支路电流是总电流的Q倍，设R<<L(a)电路发生谐振时，输入阻抗达最大值：（2）谐振特点 6.3谐振电路的频率特性RjL+_串联谐振时代入上式并整理，得 其幅频特性为从幅频特性曲线看到，通频带越窄，曲线越尖，对信号的“选择性”越好。另外，Q越大，谐振曲线越尖。当稍微偏离谐振点时，曲线就急剧下降，电路对非谐振频率下的信号具有较强的抑制能力，所以选择性好。因此，Q是反映谐振电路性质的一个重要指标。选择性(selectivity) 讨论由纯电感和纯电容所构成的串并联电路：6.4串并联电路的谐振(a)L1L3C2(b)L1C2C3上述电路既可以发生串联谐振(Z=0)，又可以发生并联谐振(Z=)。可通过求入端阻抗来确定串、并联谐振频率。对(a)电路，L1、C2并联，在低频时呈感性。随着频率增加，在某一角频率1下发生并联谐振。>1时，并联部分呈容性，在某一角频率2下可与L3发生串联谐振。 对(b)电路L1、C2并联，在低频时呈感性。在某一角频率w1下可与C3发生串联谐振。w>w1时，随着频率增加，并联部分可由感性变为容性，在某一角频率w2下发生并联谐振。定量分析：(a)当Z(w)=0，即分子为零，有：(a)L1L3C2 可解得：当Y(w)=0，即分母为零，有：可见，w1w1，滤去高频，得到低频。CRC2C3L1+_u1(t)+_u2(t) 1.3.1有理数的加法 1.理解有理数加法法则；2.利用加法法则正确地进行有理数的加法运算.学习目标: 在小学，我们学过正数及0的加法运算．学过的加法类型是正数与正数相加、正数与0相加．引入负数后，加法的类型还有哪几种呢？思考 结论：共三种类型.即：（1）同号两个数相加；（2）异号两个数相加；（3）一个数与0相加． 一个物体向左右方向运动，我们规定向右为正，向左为负．比如：向右运动5m记作+5m，向左运动5m记作－5m．（1）如果物体先向右运动5m，再向右运动了3m，那么两次运动后和的结果是什么？能否用算式表示？(+5)+(+3)=8-1012345678+5+3＋8 （2）如果物体先向左运动5m，再向左运动3m，那么两次运动后和的结果是什么？能否用算式表示？－3－5(－5)＋(－3)＝－8＋－8－8－7－6－5－4－3－2－101 根据以上两个算式能否尝试总结同号两数相加的法则？(＋5)＋(＋3)＝8(－5)＋(－3)＝－8归纳法则注意关注加数的符号和绝对值同号两数相加，取相同符号，并把绝对值相加．结论： 利用数轴，求以下三次运动的结果，并用算式表示。（1）如果物体先向左运动3m，再向右运动5m，那么两次运动和的结果怎么样？如何用算式表达？（2）如果物体先向右运动3m，再向左运动5m，那么两次运动和的结果怎么样？如何用算式表达？（3）如果物体先向右运动5m，再向左运动5m，那么两次运动和的结果怎么样？如何用算式表达？ 根据以上三个算式能否尝试总结异号两数相加的法则？注意关注加数的符号和绝对值绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0．结论：(－3)＋5=23＋(－5)=－2(－5)＋5=0 结论：一个数同0相加，仍得这个数.思考 （1）同号两数相加，取相同符号，并把绝对值相加．（2）绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0．（3）一个数同0相加，仍得这个数.有理数加法法则： 解：（－3）＋（－9）=-（3+9）=-12例1计算：（1）（－3）＋（－9）（2）（－4.7）＋3.9解：（－4.7）＋3.9=-（4.7-3.9）=-0.8先定符号，再算绝对值 练习1计算 1．有理数的加法法则是什么？2．进行有理数的加法运算时需要注意哪几个步骤？归纳小结 教科书习题１.３第1题．布置作业'