最新高职《机械设计基础》课件1课件PPT.ppt 122页

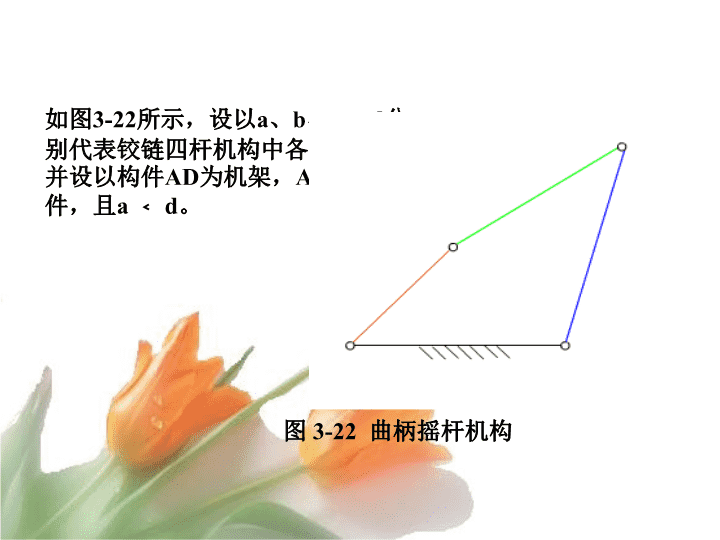
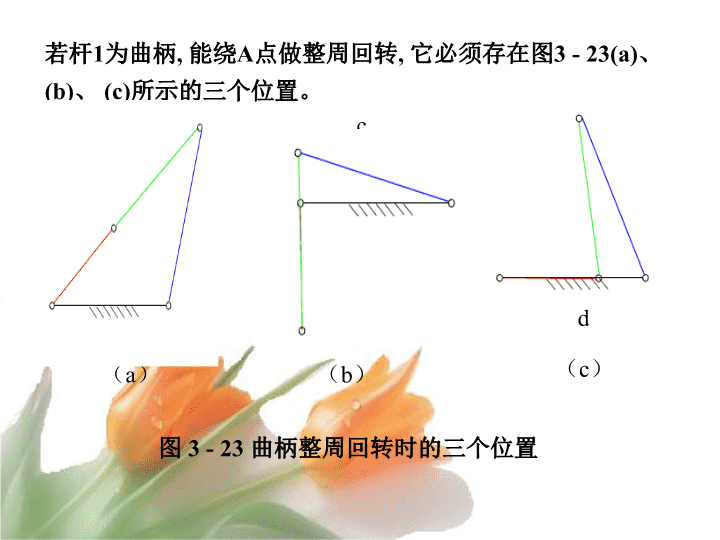
'高职《机械设计基础》课件1 图3-22曲柄摇杆机构如图3-22所示，设以a、b、c、d分别代表铰链四杆机构中各杆的长度，并设以构件AD为机架，AB为原动件，且a﹤d。abcd abcdabcdabcd图3-23曲柄整周回转时的三个位置（a）（b）（c）若杆1为曲柄,能绕A点做整周回转,它必须存在图3-23(a)、(b)、(c)所示的三个位置。1 根据有曲柄的条件可得推论：(1)取与最短杆相邻的杆件为机架,两连架杆中一个为曲柄,另一个为摇杆,则得曲柄摇杆机构；(2)取最短杆为机架,两连架杆同时成为曲柄,则得双曲柄机构；(3)取与最短杆相对的杆件为机架,两连架杆都不能整周回转,则得双摇杆机构。若最短杆与最长杆的长度之和大于其余两杆长度之和时，只能得到双摇杆机构。 3.6.2、压力角和传动角图3-24所示的曲柄摇杆机构中,如不考虑构件的重力、摩擦力和惯性力等,则连杆BC为二力杆,曲柄驱动力通过BC杆作用于摇杆CD上C点的力F是沿BC方向的,F可分解成两个分力Ft和Fn：Ft=Fcosα=FsinγFn=Fsinα=Fcosγ图3-24 F可分解成两个分力Ft和Fn：Ft=Fcosα=FsinγFn=Fsinα=Fcosγ式中α为F的作用线与其作用点(C)点速度(Vc)方向所夹的锐角,称压力角;它的余角γ(即连杆与摇杆之间所夹的锐角)称为传动角.。图3-24 对于曲柄滑块机构,当主动件为曲柄时,最小传动角出现在曲柄与机架垂直的位置,如图3-25所示。对于图3-26所示的导杆机构,由于在任何位置时主动曲柄通过滑块传给从动件的力的方向与从动杆上受力点的速度方向始终一致,因此传动角始终等于90°。 图3-25曲柄滑块机构γmin的位置 图3-26导杆机构γmin的位置 3.6.3.急回特性(1)极位夹角：图3-27所示的曲柄摇杆机构中,在主动件曲柄AB回转一周的过程中,有两次与连杆BC共线,做往复变速摆动的从动件摇杆CD分别处于左右两个极限位置C1D、C2D,其摇杆摆角为ψ。摇杆在两极限位置时,曲柄的两个对应位置所夹的锐角θ称为极位夹角。 图3-27 (2)急回特性：曲柄逆时针从AB1转到AB2,转过角度φ1=180°+θ,摇杆从C1D转到C2D所需时间为t1,C点的平均速度为v1。(3)行程速比系数:通常用行程速度变化系数K(简称行程速比系数)来表示急回特性,即从动件回程平均速度从动件工作行程平均速度(3-5)(3-6) 上式表明,在曲柄摇杆机构中,有无急回特性取决于极位夹角θ,θ值越大,K值越大,急回特性越明显。图3-28(a)、(b)分别表示偏置曲柄滑块机构和摆动导杆机构的极位夹角θ。当曲柄为原动件并等速回转时,滑块和导杆具有急回特性。 图3-28有急回特性的机构 3.6.4.死点位置如图3-29所示的曲柄摇杆机构,当CD为原动件而曲柄AB为从动件时,在曲柄与连杆共线的位置出现传动角γ等于0°的情况,这时连杆作用于从动曲柄的力通过曲柄的传动中心A,此力对A点不产生力矩,因此,无论连杆BC对曲柄AB的作用力有多大,都不能使曲柄转动。 图3-29曲柄摇杆机构死点位置 机构的这种位置称为死点位置(图中虚线所示位置)。四杆机构中有无死点位置,取决于从动件是否与连杆共线。对曲柄摇杆机构而言,当曲柄为原动件时,摇杆与连杆无共线位置,不出现死点。对于传动机构,设计时必须考虑机构顺利通过死点位置的问题,如利用构件的惯性作用,使机构通过死点。缝纫机就是借助带轮的惯性使机构通过死点位置的,如图3-30所示。 图3-30缝纫机踏板机构 工程上有时也利用死点位置提高机构工作的可靠性。例如图3-31所示的飞机起落架,当机轮着陆时,BC杆和CD杆共线,机构处于死点位置,即使轮子上受到很大的力,构件BC也不会使CD杆转动(起落架不会折回),使飞机着陆可靠。又如图3-32所示的钻床工件夹紧装置,当工件被夹紧后,BCD成一条直线,机构处于死点位置,无论工件的反力多大,夹具也不会自行松脱。 图3-31飞机起落架死点 图3-32钻床夹具的死点 3.7平面四杆机构的设计平面连杆机构的设计主要是根据给定的运动条件选定机构的形式,确定各构件的尺寸参数。有时为了使机构设计可靠、合理,还应考虑辅助条件,即机构的几何条件和动力条件(如最小传动角γmin)。平面连杆机构设计的基本问题归纳为两类: 按照给定的运动规律(位置、速度、加速度)设计四杆机构；(2)按照给定的点的运动轨迹设计四杆机构。对于上述两类基本问题的设计方法有图解法、实验法和解析法。图解法直观,实验法简便,解析法精确。本章重点介绍图解法。 3.7.1、图解法1.按给定连杆位置设计四杆机构如图3-33所示,已知连杆BC的长度lBC和依次所处的三个位置B1C1、B2C2、B3C3,试设计该四杆机构。设计分析:由图3-33可知,B1、B2、B3三点是在以铰链A点为圆心的圆弧上运动的点,故用已知圆弧上的三点求圆心的方法,可求出铰链中心点A、D。设计步骤: (1)作B1、B2和B2、B3连线的垂直平分线b12、b23,其交点为固定铰链中心A的位置。(2)作C1、C2和C2、C3连线的垂直平分线c12、c23,其交点为固定铰链中心D的位置。(3)连接A、B1、C1、D,就是所求的铰链四杆机构。 图3-33给定连杆位置设计四杆机构 2.按给定的行程速比系数设计四杆机构给定了行程速比系数K,就是给定了四杆机构急回运动的条件,从而确定了极位夹角θ。根据极位夹角和其他一些限制条件,可用图解法方便地作出曲柄摇杆机构、曲柄滑块机构及摆动导杆机构。 1)设计曲柄摇杆机构设已知摇杆CD长度为c、摆角ψ和行程速比系数K,试设计该曲柄摇杆机构。该设计的关键是确定固定铰链A的位置。设计步骤如下： (1)计算极位夹角θ。按式(3-6)，有 (2)作摇杆的两极限位置。任选点D作为摇杆回转中心位置,选取适当的长度比例尺μL,根据已知的摇杆长c和摆角ψ作出摇杆的两个极限位置C1D和C2D,如图3-34(a)所示。图3-34(a) (3)作辅助圆。连接C1、C2,并作与C1C2成90°-θ的两直线交于O点,则∠C1OC2=2θ。以O点为圆心,以OC1为半径作辅助圆。如图3-34（b）图3-34（b） (4)求曲柄、连杆的长度。设曲柄、连杆实际长度分别为a、b,在圆上任取一点A为铰链中心,并连接AC1和AC2,量得AC1和AC2的长度,据此求出曲柄、连杆的长度为(5)求其他杆长度。机架AD的长度可直接量得,乘以比例尺μL即为实际尺寸。 图3-35按行程速比系数K设计 2)设计摆动导杆机构设已知机架AC的长度d和行程速比系数K,试设计摆动导杆机构。设计分析:由图3-36可看出,摆动导杆机构的极位夹角θ与导杆的摆角ψ相等。设计导杆机构的实质就是确定曲柄长度lAB。设计步骤:(1)计算极位夹角θ。 (2)作导杆的两极限位置。任选C点为固定铰链中心,以ψ=θ=∠mCn,作出导杆的两极限位置Cm和Cn。(3)确定A点及曲柄长度。 图3-36摆动导杆 3.8杆件的轴向拉伸与压缩3.8.1轴向拉伸与压缩的概念与实例工程实际中，有很多发生轴向拉伸和压缩变形的杆件，如联接钢板的螺栓（见图3-37(a)），在钢板反力作用下，沿其轴向发生伸长（见图3-37(b)），称为轴向拉伸；托架的撑杆CD（见图3-38(a)）在外力的作用下，沿其轴向发生缩短（见图3-38(b)），称为轴向压缩。产生轴向拉伸（或压缩）变形的杆，简称为拉（压）杆。 图3-37 图3-38 3.8.2轴力与轴力图一、内力与截面法(1)内力。构件在外力（主动力和约束反力）作用下产生变形，材料内部各部分之间的相对位置发生了改变，其相互作用力也发生了改变。这种由外力引起的材料内部各部分之间相互作用力的改变量，称为内力，也称为附加内力。这种内力随外力的增加而增大，到达某一限度时，杆件就会被破坏，因而它与杆件的承载能力密切相关。内力分析是材料力学的基础。 (2)截面法。与理论力学中计算物系内力的方法相仿，用假想的截面将杆件截为两部分，任取杆件的一部分为研究对象，利用静力平衡方程求内力的方法称为截面法。 二、轴力与轴力图为了对拉（压）杆进行强度计算，首先分析其内力。设拉杆在外力F１、F２、F3的作用下处于平衡（图3-39(a)）。运用截面法，将杆件沿任一截面m-m假想分为两段（图3-39b)、(c)）。因拉（压）杆的外力均沿杆轴线方向，由其共线力系平衡条件可知，其任一截面内力FN的作用线也必通过杆轴线，这种内力称为轴力。常用符号FN表示。 图3-39 轴力FN的大小由平衡条件确定，取左段为研究对象，则∑Fx=0FN-F1+F2=0得若取右段为研究对象，则得 由整体平衡∑Fx=0F2+F3-F1=0得F3=F1-F2故FN′=F1-F2,显然有FN=FN′=Ｆ1-F2。由上面的计算可知：任一截面上的轴力，等于截面一侧杆上所有外力的代数和。即FN=截面一侧所有外力的代数和 为保证无论取左段还是右段作研究对象，所求得的同一横截面上轴力正负号一致，对轴力的正负号规定如下：轴力的方向与所在横截面的外法线方向一致时，轴力为正；反之为负。即杆受拉时轴力为正，受压时为负。对应于上述轴力正负号的规定，可得出由外力直接计算拉（压）杆某截面上轴力的外力符号规定。即产生拉伸（或背离研究截面）的外力为正，产生压缩（或指向研究截面）的外力为负，假设式中FN为正方向。 当杆受到多于两个的轴向外力作用时，在杆不同位置的横截面上的轴力往往不同。轴力FN将是横截面位置坐标x的函数，即FN=FN(x)。用平行于杆轴线的x坐标表示杆各横截面的位置，垂直于杆轴线的FN表示相应截面上的轴力，这样绘出轴力沿杆轴线变化的函数图像，称为轴力图。 【例4.1】设阶梯杆自重不计（图3-40(a)），受外力如图所示，试画出其轴力图。图3-40 3.8.3轴向拉（压）时横截面上的应力一、应力的概念确定了杆的内力后，还不能解决杆件的强度问题。经验告诉我们，材料相同，直径不等的两根直杆，在相同的拉力P作用下，内力相等。当力P增大时，直径小的杆必先断，这是由于内力仅代表内力系的总和，而不能表明截面上各点受力的强弱程度，直径小的杆因截面积小，截面上各点受力大，因此先断。所以，需引入表示截面上某点受力强弱程度的量——应力，作为判断杆件强度是否足够的量。 为了研究杆件截面a-a上任一点k的应力，如图3-41(a)所示，围绕点k取一微面积称为ΔA上的平均应力。一般情况下，内力在截面上分布并不均匀，平均应力Pm的值随ΔA的大小而改变。只有当ΔA→0时，Pm的极限值P方能代表k点受力强弱程度。故截面a-a上k点的应力为 图3-41 应力P是矢量，通常将其分解为垂直于截面的分量σ和与截面相切的分量τ（图3-41(b)）。σ称为正应力，τ称为切应力。应力的国际单位是Pa，1Pa=1N/m2，常用单位为MPa和Gpa，1Mpa=106Pa，1Gpa=109Pa。 二、轴向拉（压）时横截面上的应力欲求横截面上的应力，必须知道内力系在横截面上的分布规律。而力与变形有关，因此我们通过对杆进行轴向拉（压）实验，来观察和分析杆的变形。取一等截面直杆，在杆表面画两条横截面的边界线（ab和cd）和许多与杆轴线平行的纵向线（图3-42(a)）。然后在两端沿轴线施加拉力F，使杆件产生拉伸变形（图3-42(b)），可发现：①横向线ab和cd仍为直线，只是沿轴线发生了平移，ab和cd分别移至a′b′、c′d′，但仍垂直于杆轴线；②各纵向线发生伸长，且伸长量相同。 图3-42 根据上述现象可作如下假设：横截面变形前为平面，变形后仍为平面，仅沿轴向发生了平移，此假设称为平面假设。根据平面假设，任意两横截面间的各纵向纤维的伸长相同，即变形相同。由此可知：它们受力也应相等，内力在横截面上均匀分布。即横截面上各点处的应力大小相等，方向沿杆轴线，垂直于横截面，故为正应力。如图3-42(c)所示，计算公式为式中，FN为横截面上的轴力，A为横截面面积。正应力的正负号规定与轴力相同，即拉应力为正，压应力为负。 3.8.4轴向拉（压）时的变形一、纵向线应变与横向线应变如图3-43所示，设l、d为等直杆变形前的长度与直径，l1、d1为直杆变形后的长度和直径，则纵向变形：Δl=l1-l(a)横向变形：Δd=d1-d(b)Δl与Δd称为绝对变形，即总的变形量。拉伸时Δl>0，Δd<0；压缩时Δl<0，Δd>0。 图3-43 为了消除杆件原尺寸对变形大小的影响，用单位长度内杆的变形量，即线应变来衡量杆件的变形程度。与上述两种绝对变形相对应的纵向线应变ε和横向线应变ε′为线应变表示的是杆件的相对变形，是一个量纲为一的量。由式（c）、（d）可知：拉伸时ε>0，ε′<0;压缩时则相反，ε<0，ε′>0。总之，ε与ε′符号相反。 二、泊松比实验表明：当应力未超过某一限度时，横向线应变ε′与纵向线应变ε之间存在正比关系，且符号相反，即ε′=-με式中，比例常数μ称为泊松系数或泊松比，其值与材料有关。 三、胡克定律英国科学家胡克通过实验，发表了力与变形的关系：当杆横截面上的正应力不超过某一限度时，杆的绝对变形Δl与轴力FN、杆长l成正比，与杆的横截面积A成反比，即引入比例系数E，则（3-7） 式（3-7）称为胡克定律。式中系数E称为弹性模量，单位为GPa，其值随材料不同而异。当FN、l和A的值一定时，E值愈大，则Δl愈小，说明E的大小表示材料抵抗拉（压）弹性变形的能力，是材料的刚度指标。FN、l一定时，EA值愈大，Δl愈小，说明EA表示杆件抗拉、压变形能力的大小，称为杆的抗拉（压）刚度。 式(3-7)可改写为即或式(3-8)是胡克定律的又一表达形式。它表明当应力未超过某一限度时，应力与应变成正比。（3-8） 应用胡克定律时应注意：（1）杆的应力未超过某一极限。（2）ε是沿应力σ方向的线应变。（3）在长度l内，其FN、E、A均为常数。 3.8.5金属材料在拉伸与压缩时的力学性能一、拉伸试验和应力-应变曲线拉伸试验是确定材料力学性能的基本试验。国家标准GB228-87规定，常用圆截面拉伸标准试件如图3-44所示，其中l为试件工作长度，称为标距，标距l与直径d之比常取l/d=10。 图3-44 图3-45 二、低碳钢拉伸时的力学性能1.弹性阶段（OA段和AA′段）σ－ε曲线的OA段为一直线，说明该段内应力和应变成正比，即满足胡克定律σ=Eε。直线OA最高点A点对应的应力值为σP，称为材料的比例极限。低碳钢的比例极限σP=190～200MPa。图3-45（b）中倾角α的正切tanα=σ/ε=E，即为直线OA的斜率，数值上等于材料的弹性模量E。 当应力超过比例极限后，图3-45（b）中AA′段已不是直线，此时材料不符合胡克定律，但只发生弹性变形。若应力值超过A′点所对应的应力值σe，则出现塑性变形。因此，σe是材料产生弹性变形的最大应力值，称为材料的弹性极限，实际上A′与A两点非常接近，故工程上对两者不作严格的区分。试件的应力从零增加到弹性极限σe的过程中，试件只产生弹性变形，故称为弹性阶段。 2.屈服阶段当应力超过σe后，σ－ε曲线上将出现一段沿水平线上、下波动的锯齿形线段BC，说明应力虽有小的波动，但基本保持不变，而应变增加，材料好像失去了抵抗变形的能力。这种应力基本保持不变，而应变显著增加的现象称为材料的屈服。BC段所对应的过程称为屈服阶段。屈服阶段的最低应力值σs称为材料的屈服极限。低碳钢的σs=220～240MPa。在屈服阶段，光滑试件的表面将出现与其轴线成45°的条纹，如图3-46(a)所示，称为滑移线。表明沿最大切应力面（45°斜截面），材料晶粒间发生相对滑移，产生了塑性变形。工程上不允许过大的塑性变形，所以屈服极限σs是衡量材料强度的重要指标。 图3-46 3.强化阶段屈服阶段之后，图3-45(b)中出现向上凸的曲线CD，这表明若要试件继续变形，必须增加应力，使材料又恢复了抵抗变形的能力。该现象称为材料的强化。CD段对应的过程为材料的强化阶段。曲线最高点D所对应的应力值称为强度极限，以σb表示。它是材料能承受的最大应力。强度极限是衡量材料强度的另一重要指标。低碳钢的σb=370～460MPa。 4.颈缩阶段当材料达到强度极限后，在试件较薄弱的横截面处发生急剧的局部收缩，出现颈缩现象，如图3-46(b)所示。由于在颈缩部分横截面面积急剧减小，试件所受拉力F逐渐降低，随后试件被拉断。这一阶段为颈缩阶段，即σ－ε曲线上的DE段。 5.延伸率和断面收缩率试件拉断后，弹性变形消失，残留下的是塑性变形。试件的长由原始长度l变为l1，用百分比表示的比值称为延伸率，即断口截面积由A变为A1，试件断口处横截面面积的相对变化率为 将其称为断面收缩率。延伸率δ、断面收缩率ψ都是衡量材料塑性性能的指标。工程上，以δ>5%的材料称为塑性材料，如钢、铜、铝等；δ<5%的材料称为脆性材料，如铸铁、玻璃等。低碳钢的δ>20%～30%，ψ>60%～70%，故低碳钢是很好的塑性材料。 3.8.6轴向拉（压）时的强度计算一、极限应力、许用应力材料破坏时的应力称为极限应力，用σ0表示。对于塑性材料，当应力达到屈服极限σs（或σ0.2）时，构件已产生明显的塑性变形，影响其正常工作，一般认为构件已被破坏。因而把屈服极限σs（或σ0.2）作为塑性材料的极限应力。对于脆性材料，断裂是脆性材料破坏的惟一标志，因此，强度极限σb是脆性材料的极限应力，即塑性材料:σ0=σs（σ0.2）脆性材料:σ0=σb 由于工程构件的受载难以精确估计，以及材质的不均匀性、计算方法的近似性和腐蚀与磨损等诸多因素的影响，为了保证构件能安全可靠的工作，因此需有一定的强度储备，应将极限应力除以大于1的安全系数n，作为材料的许用应力［σ］。各种不同工作条件下构件的安全系数n的选取，可从有关工程手册和设计规范中查找。对于塑性材料，一般取n=1.2～1.3，对于脆性材料,一般取n=2.0～3.5。 二、轴向拉（压）时的强度计算为了保证拉压杆具有足够的强度，必须使杆的最大工作应力小于或等于材料在拉伸（压缩）时的许用应力［σ］，即该式称为拉（压）杆的强度条件，σmax所在的截面称为危险截面，式中FN、A分别为危险截面的轴力和横截面面积。（3-9） 根据强度条件，可解决下列三种强度计算的问题：(1)强度校核。已知杆件的材料、尺寸及所受载荷，根据式(3-9)检查杆件的强度是否足够，若式(3-9)成立，则强度足够，否则强度不够。(2)设计截面尺寸。已知所受载荷，材料的许用应力，由式A≥ＦN/［σ］，确定截面尺寸。(3)确定许可载荷。已知杆件的截面尺寸和材料的许用应力，由FN≤A［σ］，确定杆件所能承受的最大轴力，再根据静力学关系，确定结构所能承受的载荷。在强度校核计算中，可能出现最大应力稍大于许用应力的情形，设计规范规定，只要不超过5%，是允许的。 【例4.4】起重吊钩如图3-47所示，吊钩螺栓螺纹内径d=55mm，外径D=63.5mm。材料的许用应力［σ］=80MPa，载荷F=170kN，试校核吊钩螺纹部分的强度。解（1）吊钩螺纹部分所受内力为FN=170kN。（2）由于螺纹部分的轴力相同，因此横截面积最小的截面为危险截面。螺纹内径截面积最小，即 （3）校核吊钩螺纹部分的强度。所以强度足够。图3-47 3.9压杆稳定3.9.1压杆稳定的概念 2.失稳的定义压杆从直轴线状态下的稳定平衡转化为微曲状态下的不稳定平衡成为失稳。临界压力---使压杆失稳的压力称为临界压力。 3.9.2细长压杆的临界压力 3.9.4 第4章凸轮机构4.1概述4.2常用的从动件运动规律4.3盘形凸轮轮廓设计4.4凸轮机构基本尺寸的确定 4.1概述4.1.1、凸轮机构的应用凸轮是一种具有曲线轮廓或凹槽的构件，它通过与从动件的高副接触，在运动时可以获得连续或不连续的任意预期运动。凸轮机构是由凸轮、从动件和机架三个基本构件组成的高副机构。由于凸轮机构具有多用性和灵活性,因此广泛应用于机械、仪器、操纵控制装置和自动生产线中,是自动化生产中主要的驱动和控制机构。但由于凸轮机构是高副机构，易于磨损，因此只适用于传递动力不大的场合。 例一：图4-1所示为内燃机配气凸轮机构。盘形凸轮1匀速转动,通过其曲线轮廓向径的变化,驱动从动件2按内燃机工作循环的要求有规律地开启和闭合。 图4-1内燃机配气凸轮机构 图4-1内燃机配气凸轮机构模型 例二：图4-2所示为靠模车削机构，工件1回转，凸轮3作为靠模被固定在床身上，刀架2在弹簧作用下与凸轮轮廓紧密接触。当拖板4纵向移动时，刀架2在靠模板（凸轮）曲线轮廓的推动下作横向移动，从而切削出与靠模板曲线一致的工件。 图4–2靠模车削机构1234 例三：图4-3所示为一自动机床的进刀机构，当具有凹槽的圆柱凸轮1回转时，其凹槽的侧面迫使推杆2绕点C作往复摆动，从而控制刀架的进刀和退刀运动。 图4-3自动机床上的走刀机构12 图4-3自动机床上的走刀机构模型 多灶性运动神经病(multifocalmotorneuropathy，MMN)是近年来被认识的一种少见的脱髓鞘性周围神经疾病。1985～1986年，Parry等和Roth等人几乎同时报道了4例纯运动性神经病，其临床表现为进行性非对称性肢体无力，以远端受累为主，电生理特征是在运动神经上存在持续性多灶性传导阻滞(conductionblock，CB)，而感觉神经没有或只有很轻的受累。1988年，Pestronk等首次报道此病患者血清中抗神经节苷脂GMl抗体水平升高，并对免疫治疗有反应。早在1982年，Lewis等就报道了5例临床和电生理特征与此相类似的运动感觉性神经病。到目前为止，全世界报道的MMN已超过300例。 病因和发病机制发病机制不清，血清中抗神经节苷脂GMl抗体升高，应用免疫治疗可使症状有所改善，均提示此病是由免疫介导的。可能与空肠弯曲菌感染有关，已报道有3例患者在患空肠弯曲菌肠炎后出现MMN的临床表现和抗GMl抗体滴度升高，可能空肠弯曲菌的脂多糖成分(LPS)有诱导抗神经节苷脂抗体产生的作用。 病理虽然局灶性传导阻滞的病理基础是局灶性脱髓鞘，但很少在神经活检中得到证实，因为用于活检的神经大多是感觉神经(最常见为腓肠神经)，结果或是正常，或是轻度的轴索丧失、轻度的脱髓鞘或是二者同时存在。同样，感觉神经超微结构的研究也仅提示有轻度的脱髓鞘改变。只有很少患者活检做的是运动或混合神经上邻近CB的部位，病理发现为脱髓鞘改变伴洋葱球形成，没有炎性细胞浸润。 临床表现多见于男性，男∶女为2.6∶1，多数起病年龄在20～50岁，平均40岁左右，病程3个月到30年不等。多数病程呈逐渐进行性发展，个别患者病情呈阶梯性变化，前一个症状和后一个症状之间可以相隔几年，极少数可自发性缓解。到目前为止，只报道2例死亡的病例，均有20年以上的病程。多数患者病情缓慢发展，一些患者常因肌无力而使日常生活不能自理。 临床表现进行性非对称性肢体无力，没有或只有很轻的感觉症状。无力常从远端开始，早期先出现上肢症状，最常见的表现是手部肌肉无力和萎缩，症状常左右不对称，病情逐渐向近端进展，后期下肢亦受累。在不到10％的患者中，无力以近端明显或下肢症状较上肢重。肌无力症状按周围神经分布，特别是在尺神经、正中神经和桡神经分布范围内。虽然肌萎缩在受累范围内经常存在，但在疾病早期甚至后期肌萎缩可以不明显，可能是受累肌肉没有完全失神经支配的缘故。 临床表现2/3的患者有束颤和痉挛，肌颤动偶有报道。1/2的患者在相应于肌无力和肌萎缩的部位有腱反射的减低，1/4有弥漫性腱反射的减低，其余腱反射正常，少数患者腱反射可以活跃。当腱反射活跃伴发肌无力、肌萎缩和束颤时，MMN在临床上与运动神经元病很难鉴别。脑神经和呼吸肌偶有受累。虽然麻木和感觉异常等症状有时会出现，体检中只有20％的患者有很轻的感觉障碍。 电生理特征电生理特点是在运动神经常见受压部位之外存在持续性多灶性部分性传导阻滞(CB)。CB的定义为在近端和远端刺激运动神经时所得到的复合肌肉动作电位(CMAP)的波幅和(或)面积的下降不成比例。CB反映的是局灶性脱髓鞘过程，因此尽管有CB存在，运动神经传导速度可基本正常或稍有减慢，这一点与其他弥漫性脱髓鞘性神经病如肥大性周围神经病有明显的不同，后者的传导速度呈普遍性显著减慢。 电生理特征1999年，美国电诊断医学协会提出了统一的CB诊断标准。肯定的CB诊断标准是：在没有不正常的时间离散(temporaldispersion，TD）时，近端CMAP波幅与远端相比，在上、下肢神经分别下降最少达50％和60％。可能的CB是：当存在增加的TD时，CMAP出现上述相同的波幅下降，或者是没有不正常的TD，低于上述标准10％的波幅下降。 电生理特征运动性CB可以发生于任何一根或多根周围神经，也可发生于一根神经的多个不同节段，由此称之为“多灶性”。最常受累的神经是上肢的尺神经、正中神经和下肢的腓神经。运动神经传导速度基本正常或轻度减慢，其他的脱髓鞘特征如远端潜伏期和F波潜伏期的轻度延长，不正常的时间离散等在运动神经上也经常存在，提示运动神经纤维也同时存在轻度的弥漫性脱髓鞘改变。 电生理特征另一个典型的电生理特征是即使在有运动性CB的神经上感觉传导检查也正常。这种选择性运动神经受损害的机制尚不清楚。肌电图检查可以见到纤颤、束颤和运动单位电位波幅和时限的增加，通常局限于有CB的神经支配的肌肉，这一点可与运动神经元病相鉴别，后者此种异常广泛存在，可以在临床正常的肌肉中见到。 实验室检查2/3的患者CSF检查结果正常，1/3脑脊液蛋白含量可轻度增高(一般低于80mg/dl，偶尔可达l00mg/d1)，这一点可帮助鉴别MMN和CIDP，CIDP时CSF蛋白常明显升高。抗GMlIgM抗体的存在对鉴别MMN和下运动神经元综合征有帮助，抗GMlIgM抗体阳性有助于确定MMN的诊断，而阴性结果不能排除此病的诊断。 诊断当患者表现为以周围神经分布的慢性进行性肌无力、肌萎缩，症状左右不对称，以肢体远端受累为主，没有或有很轻的感觉症状时，应想到MMN的可能。确诊必须做神经电生理检查，特征性发现是1根或多根运动神经局灶性传导阻滞而相应神经的感觉传导检查正常，其他异常如远端潜伏期和F波潜伏期的轻度延长，传导速度的轻度减低，不正常的时间离散等在运动神经上也常见到，对诊断有一定的价值。血清抗神经节苷脂GMl抗体的升高对诊断有帮助。 鉴别诊断CIDP从临床上讲，CIDP的肌无力常为对称性且影响肢体的近端，而MMN无力的典型表现是远端性且非对称性。CIDP常见感觉运动同时受累，而MMN以运动症状为主，无感觉症状或有很轻的感觉受累。但是，CIDP有时也会表现为纯运动性或(和)非对称性。从病程上来讲，CIDP常有缓解复发，而MMN呈进行性发展，不经治疗很少出现缓解。从电生理上讲，CIDP的特征是广泛的运动和感觉传导速度的减慢，伴远端潜伏期的延长，反映了弥漫性而非局灶性脱髓鞘过程。同样，脱髓鞘伴洋葱球样形成、水肿和炎症细胞浸润经常出现在CIDP患者的腓肠神经活检中，而MMN的神经活检中常看不到。CIDP的脑脊液蛋白常升高，而多数MMN的脑脊液蛋白正常，虽然血清抗神经节苷脂抗体最早是在MMN中发现，但在CIDP中偶尔也可见到。类固醇激素和血浆置换对一部分CIDP患者有效，而对MMN不仅无效，有时还会加重病情。 鉴别诊断运动神经元病运动神经元病是上、下运动神经元的慢性变性疾病，而MMN主要是运动神经的局灶性脱髓鞘改变，因此MMN一般不会出现脑神经和上运动神经元受累的表现。运动神经元病多数病情发展较MMN快。运动神经元病时肌无力是按脊髓的节段分布的，而在MMN的早期，肌无力严格按周围神经分布。例如，在正中神经支配的大鱼际肌(C8～T1)可有很明显的无力，而在同一脊髓节段尺神经支配的肌肉可以完全正常。运动神经元病肌电图检查时，即使在临床上未受累的肌肉也有广泛的失神经电位，而MMN的异常电位通常局限于有CB的神经支配的肌肉。与MMN相比，运动神经元病偶尔也可发现抗GMl抗体的升高，特别是在脊肌萎缩症时，应用免疫治疗后，一些患者的症状也可改善。因此，当运动神经元病患者发现高滴度抗GMl抗体且以下运动神经元受累为著时，可给予IVIg或免疫抑制剂试验性治疗。 治疗单独的皮质类固醇激素或合并血浆置换、免疫抑制剂的治疗，结果只有很少的患者(1l％)有效；免疫球蛋白治疗对于改善临床症状和体征、减轻部分神经运动传导阻滞有确实疗效；干扰素-βla(IFN-β1a)对少数MMN患者有效。'