最新2019年第4章--控制系统的设计与仿真--MATLAB控制系统设计与仿真-教学课件PPT课件.ppt 274页

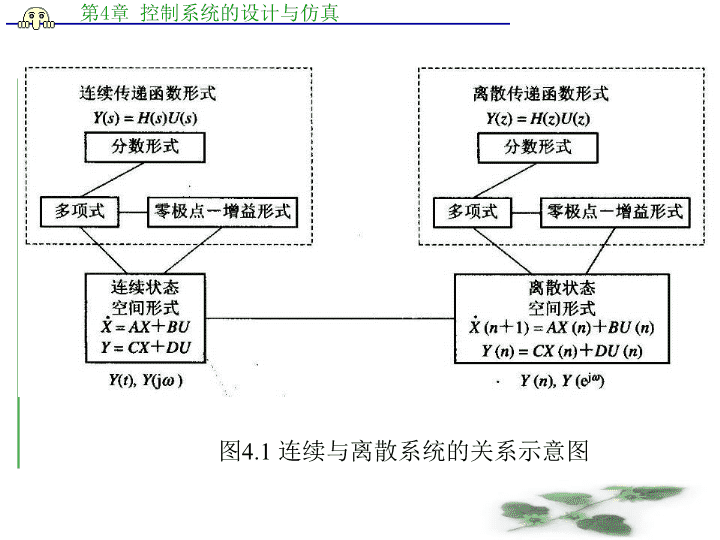
'2019年第4章--控制系统的设计与仿真--MATLAB控制系统设计与仿真-教学课件 4.1系统建模与仿真框图的创建4.1.1问题描述众所周知,现实世界中存在着各种不同的控制系统。对于线性时不变（LTI）系统,一般可以分为连续和离散系统。MATLAB中为用户提供了丰富的针对各种系统的建模手段。图4.1显示了MATLAB中各种线性时不变（LTI）系统之间的转换关系。 图4.1连续与离散系统的关系示意图 %创建系统的状态空间模型disp(′StateSpaceModels′)km=k/m;A1=［01;-km-c(1)/m］,A2=［01;-km-c(2)/m］A3=［01;-km-c(3)/m］,A4=［01;-km-c(4)/m］B=［01/m］′,C=［10］,D=［0］sys1s=ss(A1,B,C,D);sys2s=ss(A2,B,C,D);sys3s=ss(A3,B,C,D);sys4s=ss(A4,B,C,D); %仿真系统的脉冲和阶跃响应（时域）t=0:.2:15;y1=impulse(sys1s,t);y2=impulse(sys2s,t);y3=impulse(sys3s,t);y4=impulse(sys4s,t);figure(1)subplot(221),plot(t,y1,′r′),title(′CriticalDamping―Impulse′),gridxlabel(′Time′),ylabel(′SystemResponse′)subplot(222),plot(t,y2,′r′),title(′OverDamping―Impulse′),gridxlabel(′Time′),ylabel(′SystemResponse′) subplot(223),plot(t,y3,′r′),title(′UnderDamping―Impulse′),gridxlabel(′Time′),ylabel(′SystemResponse′)subplot(224),plot(t,y4,′r′),title(′NoDamping―Impulse′),gridxlabel(′Time′),ylabel(′SystemResponse′) %y1=step(sys1s,t);y2=step(sys2s,t);y3=step(sys3s,t);y4=step(sys4s,t);figure(2)subplot(221),plot(t,y1,′r′),title(′CriticalDamping―Step′),gridxlabel(′Time′),ylabel(′SystemResponse′)subplot(222),plot(t,y2,′r′),title(′OverDamping―Step′),grid xlabel(′Time′),ylabel(′SystemResponse′)subplot(223),plot(t,y3,′r′),title(′UnderDamping―Step′),gridxlabel(′Time′),ylabel(′SystemResponse′)subplot(224),plot(t,y4,′r′),title(′NoDamping―Step′),gridxlabel(′Time′),ylabel(′SystemResponse′)disp(′hitanykeytocontinue′),pause %在Matlab中进行模型转化。对于m=k=1,系统简化的传递函数为%G(s)=1/［s^2+cs+1］=z(s)/p(s)disp(′TransferFunctionForm′)sys1t=tf(sys1s),sys2t=tf(sys2s)sys3t=tf(sys3s),sys4t=tf(sys4s)disp(′hitanykeytocontinue′),pause %将传递函数形式转化成零极点形式disp(′Zero―Pole―GainForm′)sys1z=zpk(sys1t),sys2z=zpk(sys2t)sys3z=zpk(sys3t),sys4z=zpk(sys4t)disp(′hitanykeytocontinue′),pause%演示留数定理的使用disp(′ResidueForm′)［n1,d1］=tfdata(sys1t);［n2,d2］=tfdata(sys2t);［n3,d3］=tfdata(sys3t);［n4,d4］=tfdata(sys4t); %注意tfdata命令定义元胞数组%将元胞数组转化成向量形式n1=n1{1},d1=d1{1},n2=n2{1},d2=d2{1},n3=n3{1},d3=d3{1},n4=n4{1},d4=d4{1},%使用留数定理［r1,pr1,kr］=residue(n1,d1),［r2,pr2,kr］=residue(n2,d2)［r3,pr3,kr］=residue(n3,d3),［r4,pr4,kr］=residue(n4,d4)disp(′hitanykeytocontinue′),pause %进行频域仿真,这里使用nyquist函数（参考bode,freqs等函数）w=logspace(-2,2,100);［re,im］=nyquist(sys1s,w);%SS形式re1(:,1)=re(1,1,:);im1(:,1)=im(1,1,:);g1=re1+i*im1;mag1=20*log10(abs(g1));phase1=angle(g1)*180/pi;［re,im］=nyquist(sys2s,w);%SS形式re2(:,1)=re(1,1,:);im2(:,1)=im(1,1,:);g2=re2+i*im2;mag2=20*log10(abs(g2));phase2=angle(g2)*180/pi;［re,im］=nyquist(sys3t,w);%TF形式re3(:,1)=re(1,1,:);im3(:,1)=im(1,1,:);g3=re3+i*im3; mag3=20*log10(abs(g3));phase3=angle(g3)*180/pi;［re,im］=nyquist(sys4t,w);%TF形式re4(:,1)=re(1,1,:);im4(:,1)=im(1,1,:);g4=re4+i*im4;mag4=20*log10(abs(g4));phase4=angle(g4)*180/pi;%幅值曲线figure(3)subplot(221),semilogx(w,mag1,′r′),title(′CriticalDamping′),xlabel(′frequency′),ylabel(′|G(jw)|indb′)subplot(222),semilogx(w,mag2,′r′),title(′OverDamping′),xlabel(′frequency′),ylabel(′|G(jw)|indb′) subplot(223),semilogx(w,mag3,′r′),title(′UnderDamping′),xlabel(′frequency′),ylabel(′|G(jw)|indb′)subplot(224),semilogx(w,mag4,′r′),title(′NoDamping′),xlabel(′frequency′),ylabel(′|G(jw)|indb′)disp(′hitanykeytocontinue′),pause%频率曲线figure(4)subplot(221),semilogx(w,phase1,′r′),title(′CriticalDamping′),xlabel(′frequency′),ylabel(′angle′) subplot(222),semilogx(w,phase2,′r′),title(′OverDamping′),xlabel(′frequency′),ylabel(′angle′)subplot(223),semilogx(w,phase3,′r′),title(′UnderDamping′),xlabel(′frequency′),ylabel(′angle′)subplot(224),semilogx(w,phase4,′r′),title(′NoDamping′),xlabel(′frequency′),ylabel(′angle′)disp(′hitanykeytocontinue′),pause %绘制系统Nichols图（对数坐标形式）figure(5)subplot(221),plot(phase1,mag1,′r+′),title(′CriticalDamping′),xlabel(′angle′),ylabel(′|G(jw)|indb′),gtext(′w=0′)subplot(222),plot(phase2,mag2,′r+′),title(′OverDamping′),xlabel(′angle′),ylabel(′|G(jw)|indb′),gtext(′w=0′)subplot(223),plot(phase3,mag3,′r+′),title(′UnderDamping′), xlabel(′angle′),ylabel(′|G(jw)|indb′),gtext(′w=0′)subplot(224),plot(phase4,mag4,′r+′),title(′NoDamping′),xlabel(′angle′),ylabel(′|G(jw)|indb′),gtext(′w=0′)disp(′hitanykeytocontinue′),pause %绘制Nyquist图(实部-虚部形式)figure(6)subplot(221),plot(re1,im1,′r+′),title(′CriticalDamping′),xlabel(′Real′),ylabel(′Imag′),gtext(′w=0′)subplot(222),plot(re2,im2,′r+′),title(′OverDamping′),xlabel(′Real′),ylabel(′Imag′),gtext(′w=0′) subplot(223),plot(re3,im3,′r+′),title(′UnderDamping′),xlabel(′Real′),ylabel(′Imag′),gtext(′w=0′)subplot(224),plot(re4,im4,′r+′),title(′NoDamping′),xlabel(′Real′),ylabel(′Imag′),gtext(′w=0′)disp(′hitanykeytocontinue′),pause %直接使用Nyquist函数绘制Nyquist图figure(7)subplot(2,2,1),nyquist(sys1s,w),title(′CriticalDamping′),subplot(2,2,2),nyquist(sys2s,w),title(′OverDamping′),subplot(2,2,3),nyquist(sys3s,w),title(′UnderDamping′), subplot(2,2,4),nyquist(sys4s,w),title(′NoDamping′),disp(′hitanykeytocontinue′),disp(［′hitcntrl-ctogetoutofthefileforinteractiveanalysis′］),pause%使用Simulink框图（文件名为mdemosl.mdl,如图4.2所示）进行仿真clearall%清空所有内存 m=1,k=1,c=1.2%定义常数disp(′DatafromgraphicalSimulinkmodel′)%计算线性化模型［A,B,C,D］=linmod(′mdemosl′),syss=ss(A,B,C,D);sysz1=zpk(syss),syssm=minreal(syss),sysz2=zpk(syssm)diaryoff%关闭二进制文件 图4.2MassSpringDashpot系统仿真框图 4.1.2物理模型例4.1中研究的对象是一个简单的物质交换机械系统,可以用微分方程表示成(4.2)其中,y(t)是系统的瞬时交换的质量,k和c分别为比例常数。如果取状态变量x1=y和x2=dy/dt,则可以得到系统的状态方程形式： 可以看出,矩阵A、B、C和D可以看成LTI系统的标准状态方程形式,于是式（4.3）可以写成(4.3) 4.1.3时域仿真一般对控制系统进行时域仿真可以采用impulse、step和lsim函数,这些函数用来处理系统的状态空间描述。例如,对于输入信号u(t),系统的动态仿真可表示成sys=ss(A,B,C,D)［Y,T,X］=lsim(sys,U,t,xo) 当然,这些函数也可以处理系统的频域表达形式,这时,LTI系统可以通过下式表示sys=tf(num,den)作为一个典型的例子,例4.1使用了impulse和step函数来仿真系统的时域特性。图4.3和图4.4分别为例4.1执行的仿真结果。 图4.3典型二阶系统的脉冲响应曲线 图4.4典型二阶系统的阶跃响应曲线 4.1.4模型转换LTI系统的频域描述可以用传递函数表示为Y(s)=G(s)U(s)(4.5)系统的传递函数矩阵为(4.6)对于例4.1研究的简单SISO机械系统,其传递函数可以写成简单的标量形式(4.7) 但是对于多输入多输出（MIMO）系统而言,其传递函数描述就有些复杂了,这时MATLAB中的模型转换函数可以发挥作用,它可以完成系统在状态方程形式与传递函数形式之间的互换,同时也可以将传递函数形式转换成零极点-增益形式。相关的函数包括sys1=ss(A,B,C,D)sys2=tf(sys1)sys3=zpk(sys2) 我们也可以采用ssdata、tfdata和zpkdata等命令将存储在与一个指定LTI对象相联的数据结构中的信息抽取出来。例如［num,den］=tfdata(sys2)返回LTI对象sys2的分子和分母多项式系数,num与den为相应的元胞数组,其行数为输出的维数,列数等于输入的维数。其中第i行第j列元素表示从第j个输入到第i个输出的传递函数。 另一种从数据结构中得到元胞数组的方法是使用MATLAB的celldisp命令。简单的显示数据的信息,可以使用如下的命令:fieldnames(sys2)num1=sys2.num,den1=sys2.dencelldisp(num1),celldisp(den1)也可以对零极点-增益形式完成显示的操作。例如［Z,P,K］=zpkdata(sys3) 将获取LTI系统sys3每一个IO通道的零极点和增益大小。元胞数组Z、P和矩阵K的行与列分别与输出和输入的维数相同。其中第i行第j列元素表示从第j个输入到第i个输出传递函数的零极点和增益。对于单输入单输出（SISO）系统,其传递函数与零极点-增益形式可以简化成普通的分数形式，即(4.8) 4.1.5留数定理我们也可以将系统写成几个分数相加的形式,例如对于SISO的机械系统,G(s)可以写成(4.9)(4.10) r1,r2可以通过各种不同的方法计算得到。对于上述问题,MATLAB可用residue函数来完成这一运算，即［r,p,k］=residue(B,A)其中B和A为包含多项式系数的行向量,而r和p是包含留数和极点的列向量。如果B(s)比A(s)的维数大,则k(s)不为零。 4.1.6频域仿真系统的频域仿真在概念上是非常直观的,但是计算起来常常比较复杂。作为练习,读者可以针对不同的ω值,计算下面的表达式G(jω)=C［jωI-A］-1B+D(4.11)然后通常采用下列三种方法来绘制频域曲线：Bode图、Nichols图和Nyquist曲线。 MATLAB中的一些函数用来获取系统的频域信号。首先必须产生一个频率的向量。采样点的坐标通常采用对数形式,即从10d1到10d2共n个点,可以通过下面的命令来完成:w=logspace(d1,d2,n)bode和nyquist函数可以用来计算每一个频率ω所对应的G(jω)，即［MAG,PHASE］=bode(sys,w)［RE,IM］=nyquist(sys,w) 图4.5典型二阶系统的Bode幅值曲线 图4.6典型二阶系统的Bode频率曲线 图4.7 图4.8 4.1.7仿真框图及系统建立许多设计系统都可以由一些基本的组件和框图中的反馈回路组成。在有些情况下,寻找系统的等价描述和相应的状态空间矩阵是比较困难的。幸运的是,我们可以借助MATLAB从系统的Simulink仿真框图直接建立它的状态空间描述。这些工作可以通过MATLAB中的控制工具箱或Simulink的图形仿真界面来完成。 为了演示这一过程,同样考虑一下例4.1所述的简单机械系统。首先建立该系统的Simulink仿真框图,然后自动创建原系统的状态空间和整个系统的传递函数形式。下面将状态方程展开,并且进行Laplace变换(4.12) 上述拉普拉斯变换可以对应于如图4.10所示的基本模块。现在将这些模块连接起来,定义输出为Y(s)=X1(s),最后得到如图4.2所示的仿真框图。下面我们可以使用linmod函数来计算LTI系统的状态矩阵：［A,B,C,D］=linmod(′mdemosl′)计算的结果与前面得到的结果一致。 图4.9MATLAB计算产生的典型二阶系统的Nyquist曲线 图4.10Laplace变换下的基本模块 4.2控制系统设计在经典控制系统设计中通常以线性系统模型为研究对象。对于一个线性时不变（LTI）系统,其状态方程可以描述为(4.13)(4.14) 这里已经假定系统的输出没有显式地包含输入变量u（即D=0）。系统（4.14）也可以表示为传递函数形式：Y(s)=G(s)U(s)G(s)=C(sI-A)-1B(4.15)一个LTI系统的控制系统方框图如图4.11所示。 图4.11系统的线性状态方程模型 4.2.1经典比例控制器在经典控制系统的例子中,首先来看一下图4.12所示的一个简单的闭环系统。对于一个SISO系统而言,系统传递函数G(s)仅仅是式（4.15）所示的标量函数,该传递函数嵌入在图4.12所示的方框图中。反馈回路包含传感器传递函数H(s),而控制器部分只有简单的增益环节Kc组成,rd是闭环系统期望的响应或参考点。 图4.12SISO系统的经典比例控制器框图 图4.12所示闭环系统的传递函数可以写成(4.16)其中,Gc(s)为闭环传递函数,Kc是经典比例增益。对于单位反馈情况有H(s)=1,Gc(s)可以简化为(4.17)下面是标量输入函数的时域表示u(t)=Kc(rd(t)-y(t))=Kc(rd(t)-CTX(t))(4.18) 从而式（4.14）可以写成(4.19)这里的参考点rd成为系统的一个独立输入变量。 既然控制器只有唯一的参数Kc需要确定,因此该系统的控制器设计比较简单。闭环系统的暂态响应由状态方程系数矩阵的特征值或者整个系统的根极点确定。我们可以在时域中通过选择合适的控制参数Kc,使得(A-KcBCT)的特征值产生期望的暂态响应（上升时间、最大超调量等）。与此类似,也可以在传递函数中通过选择合适的控制参数Kc来设计式（4.17）系统的根极点位置。这两种设计方法是等价的。我们知道Gc(s)的极点是1+KcG(s)的根,因此可以将极点配置方程看作控制增益Kc的根。运用根轨迹方法可以确定满足设计要求的控制参数。 4.2.2状态反馈控制器上述经典控制器的主要不足是系统仅有唯一的控制参数Kc可供调整,而对于N维控制系统,系统开环矩阵具有N个特征值或者开环传递函数具有N个极点,即det(A-λI)=0或det(sI-A)=0(4.20)要想将所有这些系统根极点调整到需要的位置,控制器至少需要N个独立变量,因此仅仅将系统输出信号进行反馈将不能满足控制器设计的要求。一个自然的想法就是将系统的所有状态变量X都进行反馈,这就产生了状态反馈控制器。 对于SISO系统,状态反馈后的系统输入变成u(t)=rd(t)-KTsX(t)(4.21)Ks称为系统的反馈系数。这样,闭环系统的状态方程可以写成(4.22)闭环系统的框图如图4.13所示。同时,图4.11所示的状态反馈系统变成图4.14所示的仿真框图。 图4.13SISO系统的状态反馈控制器 图4.14 4.2.3完全可控性为了设计具有状态观测器的状态反馈控制器,让我们首先熟悉有关系统可控性的定义。假设一个SISOLTI系统由式（4.23）描述(4.23) 如果该系统能够构造一个无约束的输入信号u(t),使得系统能够在有限的时间间隔内（t0≤t≤tf）由初始状态运动到任何其它的状态,则可以说系统在t0时刻是可控的。如果系统的每个状态都是可控的,则称该系统是完全可控的。不失一般性,假设X(tf)=0,t0=0,则(4.24)根据完全可控性的定义,有(4.25) 或者根据Sylvester积分公式有(4.26)(4.27)(4.28) 当如下矩阵非奇异时,系统满足完全可控的条件：M=［BABA2B…AN-1B］(4.30)或者(4.29) 4.2.4极点配置设计状态反馈控制器的最简单方法是采用极点配置。其基本思想是首先确定闭环系统N个根极点的期望位置,然后设计适当的反馈增益,从而将系统的极点调整到期望的位置。如果系统是完全可控的,则这一过程完全可以表示成包含N个未知参数的N个方程组的求解。所需要设计的反馈控制增益就是该方程组的解。 如果系统比较简单,则完全可以通过手工计算完成系统的极点配置,但无论是手工计算,还是通过MATLAB函数自动计算,其基本步骤都是相同的，如下所示：（1）检查系统的可控矩阵是否满秩。（2）确定闭环系统的期望极点,μ1,μ2,…,μN。（3）确定希望配置的极点位置后,可以建立期望的特征方程。 （4）最后建立闭环系统的特征方程,即(sI-(A-BKTs))=0,将（3）、（4）步建立的方程联立,由于其多项式的系数相等,由此可以建立N个位置参数的N个方程组,从而可以唯一地确定系统的反馈增益矩阵KTs。 例4.2假定SISOLTI系统的状态方程为闭环系统的期望极点为μ1,2=-1.8±2.4j,试设计确定系统状态反馈的增益矩阵。解：首先观察开环系统的极点 可以看出,系统开环极点为s1,2=±4.539,系统是不稳定的。闭环系统的期望极点是由期望的系统暂态响应特性（上升时间、读者可以验证,μ1,2=-1.8±2.4j的闭环极点将产生较好的动态特性（大约10%的最大超调量和大约0.6s的上升时间）。因此,期望的闭环系统极点是不唯一的。下面在已经确定期望闭环系统极点的情况下来设计系统的反馈增益矩阵。Step1：验证系统的可控性。 矩阵M的秩等于N,因此系统满足完全可控性条件。Step2～3：计算期望的特征方程(s-μ1)(s-μ2)=(s+1.8-j2.4)(s+1.8+j2.4)=s2+α1s+α2=0Step4：计算闭环系统的特征方程 因此 4.2.5带全观测器的状态反馈控制设计状态反馈控制器的主要问题是要求系统的所有状态变量都是可测的。然而对于一个实际系统而言,有些状态的信号值很难测量甚至不可能直接通过传感器进行测量,或者虽然可以进行直接测量,但在经济上却要增加相应的成本。这样,如果不能得到系统的全状态向量,前面讲述的状态反馈控制就不可能实现。 解决以上问题的方法是利用系统某种数学形式的仿真来估计不能测量的状态值,这种方法称之为系统的状态观测器设计。下面假定以SISOLTI系统为研究对象,这意味着系统有唯一的可控变量和唯一的可测量。同时,假定系统输出y(t)是唯一能够测量的量,它将被引入到状态观测器中来提高状态值的估计过程。这里采用来表示状态向量X(t)的在t时刻的估计值。 状态观测器的框图如图4.15所示（注意变量xc表示。该观测器使用u(t)和y(t)作为输入量,并且输出系统状态关于时间的估计值。从框图中可以看出(4.31)这里的L为未知的增益,它是根据该子系统期望的暂态响应特性确定的,称为状态观测器的增益矩阵。对于SISO系统,L是长度为N的列向量。 图4.15SISO系统的状态观测器模型 观测器的设计过程与前面讲述的标准状态反馈控制器类似。这里的观测器的增益选择应使状态观测器的特征值是稳定的,同时使得观测器的动态变化快于整个闭环系统的动态属性。观测器的特征值由下式确定：det(sI-(A-LCT))=0(4.32)在状态反馈控制系统中加入状态观测器,可得到图4.16所示的系统框图。对于该系统,系统输入为(4.33) 如果系统模型与状态观测器模型都采用相同的状态空间矩阵A、B、CT进行描述,则对于被研究对象有将式（4.33）的输入代入上面的方程,则得到系统的完整模型(4.34)(4.35) 图4.16具有全状态观测器的状态反馈控制系统框图（SISO系统） 对于状态观测器,将式（4.33）代入式（4.31）可以得到观测器的完整模型或者(4.36)(4.37)定义误差向量将式（4.37）代入得到误差向量的动态模型(4.38)(4.39) 4.2.6完全可观性如果系统的每个状态X(t0)都可以通过y(t)一段时间的观测值来确定,则该系统被称为是完全可观的。考虑式（4.23）定义的SISOLTI系统,其时域解为(4.40)假设u(τ)=0,为方便计算,上式可以写成(4.41) 其中,CTeAt已知,y(t)可测。因此状态向量X(0)可以通过y(t)的观测值间接计算得到。对于SISO系统,方程（4.41）仅有一个方程,但包含N个未知参数。然而,由于该方程独立于时间变量,因此,在多个时刻对y(t)进行测量,可以获得多个类似的方程,将它们联立,就可以唯一确定系统的初始状态X(0)。下面给方程（4.41）两边同时乘以已知的系数矩阵,得到(4.42)(4.43)(4.44)变换方程有 将整个观测时间内的所有方程进行联立,得到(4.45)其中(4.46)最后求解方程（4.45）,得到如果W是非奇异的,X(0)可以由y(t)的观测值唯一确定,从而系统是完全可观的。再次使用Sylvester的积分公式,得到 定义(4.48)(4.49)(4.50) 4.2.7观测器增益的确定确定观测增益矩阵同样采用极点配置的方法。然而在这里,我们确定的是状态观测器误差方程的极点位置。误差极点位置的选择比较随意,但误差动态变化应该比被控系统的动态变化快一些。如果系统完全可观,则(A-LCT)的N个特征值的位置应该唯一确定观测器增益矩阵的N个元素。设计的过程如下：（1）检查系统可观矩阵是否奇异。 （2）为误差方程指定期望的极点位置（μ1,μ2,…,μN）。这些极点位置与系统的主导极点相比较应该更靠近复平面的左手边。（3）根据期望的极点位置创建期望的特征方程。（4）最后创建误差方程的特征方程,从而得到含有N个位置参数的方程组。同样，以例4.2为例来说明SISO系统状态观测器的设计过程。 例4.4用MATLAB的place函数重新设计例4.2的状态反馈控制器与例4.3中的全状态观测器。解：程序代码如下：%SFSOTEST.MSISOLTI系统的状态反馈控制器与全状态观测器的设计clearall,closeall,nfig=0;%打开二进制文件保存结果deletesfsotest.outdiarysfsotest.outdisp(′′)disp(′***SFSOTEST.OUT***DiaryFileforSFSOTEST.M′) disp(′′)%PartI.创建线性系统模型,显示其开环系统是不稳定的SetupbasedataforthelinearA=［01;20.60］;B=［01］′;%建立系统的状态空间模型C=［10］;D=［0］;disp(′StateSpaceMatricesforthePlant′)A,B,C,D %computeeigenvaluesofstatematrixforopenloopplantdisp(′Eigenvaluesofthe"OpenLoopPlant"′);%计算开环系统状态矩阵特征值ev=eig(A)%PartII.加入状态反馈控制器以稳定系统,对状态1的输出量进行仿真%检查系统的可控性disp(′ControllabilityMatrixforthissystem′),M=ctrb(A,B)disp(′RankofControllabilityMatrix′),rank(M)clp=［-1.8+2.4j-1.8-2.4j］;%计算状态反馈控制增益Ks=place(A,B,clp); disp(′Desiredclosedlooppolesforstatefeedbackcontroller′);clpdisp(′Statefeedbackgainsneededtogivedesiredpoles′);Ksdisp(′Calculatedeigenvaluesofsystemwithstatefeedback′);eig(A-B*Ks)Nv=-1.0/(C*inv(A-B*Ks)*B);%计算Nvdisp(′SetpointgainforzeroSSerror′);Nvto=0;tf=5;nfig=0;%对被控系统+控制器进行仿真t=linspace(to,tf,101);syscl1=ss(A-B*Ks,B*Nv,C,D);［y1,t,x1］=step(syscl1,t); nfig=nfig+1;figure(nfig)%绘制相关结果曲线subplot(2,1,1),plot(t,x1(:,1),′r-′,t,x1(:,2),′g--′),grid,title(′StatesforStateFeedbackTestCase′)xlabel(′Time′),ylabel(′StateVariables′)legend(′x1(t)′,′x2(t)′)%PartIII.加入状态反馈控制器与全状态观测器,仿真状态1的阶跃响应特性%检查系统的完全可观性disp(′ObservabilityMatrixforthissystem′),H=obsv(A,C)disp(′RankofObservabilityMatrix′),rank(H) %针对指定的观测器极点计算观测器增益op=3*clp;%观测器的速度是闭环系统的3倍L=place(A′,C′,op);L=L′;disp(′Desiredobserverpolesforstatefeedbackcontroller′);opdisp(′Estimatorgainsneededtogivedesiredpoles′);Ldisp(′Calculatedeigenvaluesofestimatorsystem′);eig(A-L*C)A11=A;A12=-B*Ks;B1=B*Nv;A21=L*C;A22=A-L*C-B*Ks;B2=B*Nv;zz=0;AB=［A11A12;A21A22］;BB=［B1;B2］;CB=［Czz*C］; %对控制系统进行仿真syscl2=ss(AB,BB,CB,D);［y2,t,x2］=step(syscl2,t);%分离系统状态与观测器的估计状态nn=max(size(A));xp2=x2(:,1:nn);xe2=x2(:,nn+1:2*nn);%绘制全观测器情况下的计算结果subplot(2,1,2),plot(t,xp2(:,1),′r-′,t,xp2(:,2),′g--′),grid,title(′StatesforStateFeedbackwithFullObserverTestCase′)xlabel(′Time′),ylabel(′StateVariables′)legend(′x1(t)′,′x2(t)′) %绘制状态估计的误差nfig=nfig+1;figure(nfig)plot(t,xp2(:,1)-xe2(:,1),′r-′,t,xp2(:,2)-xe2(:,2),′g--′),grid,title(′DifferenceBetweenPlantandObserverStates′)xlabel(′Time′),ylabel(′ErrorinStateVariables′)legend(′e1(t)′,′e2(t)′)Diaryoff%关闭二进制文件 图4.17系统模型与观测器动态性能演示 图4.17系统模型与观测器动态性能演示 图4.18状态误差的动态曲线 4.2.8对偶系统回忆前面论述的系统可控与可观性的定义，可知系统的可控性要求其可控矩阵满秩,反映的是状态矩阵A与输入矩阵B之间的关系；而系统的可观性要求其可观矩阵满秩,反映的是状态矩阵A与输出矩阵CT之间的关系。这两个概念实际上反映了控制系统的对偶原则。对于一般的MIMO系统(4.52)(4.54)(4.53) 对于系统1,其完全状态可控的充要条件是M矩阵满秩，即M1=［BABA2B…AN-1B］(4.55)系统完全状态可观性的充要条件是H*矩阵满秩，即H*1=［C*A*C*A*2C*…A*N-1C*］(4.56)对于系统2,其完全状态可控的充要条件是M矩阵满秩，即M2=［C*A*C*A*2C*…A*N-1C*］(4.57) 系统完全状态可观性的充要条件是H*矩阵满秩，即H*2=［BABA2B…AN-1B］(4.58)综上所述,给定系统的可观性可以通过其对偶系统的可控性来检验,而研究系统的可控性则可以通过其对偶系统的可观性来研究,这些性质称为系统的对偶原则。 4.3控制系统的时域仿真前一节以经典控制器和状态反馈控制器为例讲述了控制系统控制参数的设计过程。设计过程主要依据的是系统的时域特性,即闭环系统状态矩阵的特征值决定了闭环系统的暂态响应特性。控制器设计的目标是选择控制器的增益,使得闭环系统状态矩阵的特征值位于期望的极点位置。 控制器参数确定以后,下一步需要对闭环系统进行仿真。在设计过程中研究的对象一般是系统的线性化模型。而在仿真过程中,应该尽可能准确地再现实际的系统模型,这就常常要求以实际的时变或非线性系统为仿真的对象。这一节主要论述控制器参数确定以后的系统仿真过程。为简单起见,仍然以SISO系统为研究对象。其线性与非线性模型分别为(4.59)(4.60) 4.3.1经典比例控制器设计单位反馈回路的简单比例控制系统框图如图4.19所示。系统控制输入为(4.61)使用线性化模型的闭环仿真方程为(4.62)写成标准的状态方程形式(4.63) 如果采用非线性模型进行仿真,必须使用MATLAB中标准的ODE求解器来完成。为此,用户必须定义一个函数文件,MATLAB中的ODE求解器调用该函数来完成非线性系统的仿真。该函数文件包含下面的内容：（1）指定t时刻的参考输入rd(t)。（2）计算系统t时刻的输出y(t)=CTX(t)。（3）确定t时刻的输入u(t)=Kc(rd(t)-y(t))。（4）计算t时刻状态变量的导数 图4.19SISO系统的经典比例单位反馈控制框图 4.3.2状态反馈控制器带全状态观测器的状态反馈控制框图如图4.20所示。该框图类似于图4.16,不同之处在于这里的模型包括一个附加的稳态状态增益模块,其中包含一个归一化的增益变量Nr。我们再来看看该系统线性化模型与非线性模型的仿真方程,并且重新调整控制器的增益（KTs,L和Nr等）。控制规律写成(4.64) 该系统的闭环模型包括实际的系统状态X(t)以及估计的系统状态。这样,该系统具有2N个未知参数。对于线性系统模型,该系统的完整模型为被控系统模型(4.65)观测器模型(4.66)写成标准的状态方程形式为 图4.20具有全状态观测器的状态反馈控制系统 4.3.3混合控制器下面将研究一种将状态反馈控制运用到经典控制器中的例子。在这个例子中,状态反馈制器为经典控制器提供修正的参考信号。例如,对于图4.18的经典控制系统,如果选择的增益Kc不满足系统的设计要求,我们可能会手动调节参考点rd,以使系统具有更好的暂态响应特性。可以设想一种控制方案来自动为参考信号rd(t)提供实时的修正信号rdm(t),控制框图如图4.20所示。 图中左边的sum模块的输出为修正后的参考点信号,在此之后,该系统看上去就像是具有单位反馈回路和比例增益Kc的经典控制器。在这个控制方案中,状态观测器和状态反馈回路的目标是提供一个修正的参考信号,来改善经典控制系统的控制效果。这种方法称为状态反馈辅助的经典控制方法（SFACC）,也称为混合的控制器。 图4.21显示的控制系统实际上可以看作是前面讲述的状态反馈控制系统,其控制框图可以认为是从图4.20的标准形式通过某些模块变换发展而来。图4.22～4.24显示了其中的变换,主要步骤包括:（1）在系统输入前加上一个比例增益模块,并且在相应的引入回路中抵消它的影响（如图4.22所示）。 图4.21具有嵌入经典控制器的状态反馈控制框图（SFACC） （2）对系统输出y构造一个负反馈,它可以对估计输出的正反馈加以抵消（如图4.23所示）。（3）分离出经典控制器部分（图4.24中的阴影部分）。（4）最后定义修正的状态反馈增益Ksm和修正的稳态状态归一因子Nnn。(4.68)(4.69) 图4.22在SFC中加入经典控制增益 图4.23加入经典负反馈回路 图4.24分离出经典比例控制器部分 图4.21所示的SFACC控制系统与传统的状态反馈控制系统SFC（如图4.20所示）在功能上是一致的。仅有的近似存在于第(2)步,这一步假设估计的输出与实际的系统输出完全抵消。如果状态观测器设计成相对控制系统有足够快的反应时间,这种近似是可以满足要求的（对于线性模型）。 从以上的讨论中可以看出,SFC和SFACC具有相同的暂态响应。然而,SFACC算法比前者具有更好的控制效果。并且SFACC可以方便地在原先经典控制系统的基础上进行扩展,而不需要破坏原来已经存在的控制系统。这让用户可以从经典控制器直接过渡到现代控制系统。为了对SFACC控制系统进行仿真,我们假定控制规律为修正后的参考信号为将式（4.71）代入式（4.70），有（4.70）(4.71)(4.72) 与SAC控制系统类似,SFACC闭环系统既包含实际状态也包含估计状态,因此,可以获得2N个未知参数。对于线性系统模型,有系统模型为(4.73)(4.74)(4.75) 或者(4.76)写成标准的状态方程形式为其中(4.78) 4.3.4参考输入增益的调整在前面的框图中,为了减小比例控制器带来的稳态误差,引入了一个输入归一化模块。该模块的增益值可以根据下面的算式进行确定（图4.25显示了系统的简化模型）。线性模型(4.79)(4.80)控制律 系统稳态时,我们希望yss与参考点rdss相同。简化系统稳态时的状态方程为(4.81)求解该方程,得稳态时的状态向量为(4.82) 图4.25具有SS增益模块的状态反馈控制系统 稳态输出为(4.83)最后将yss=rdss代入,得到Nr的计算公式为(4.84) 4.4实例:倒摆系统的建模与仿真4.4.1引言这一节我们先看一个实际的例子。图4.26是某个倒摆系统的示意图,倒摆通过转动关节安装在驱动小车上,通过对小车施加一定的驱动,使倒摆保持一定的姿态。这是姿态控制问题的典型代表。 图4.26驱动小车上的倒摆示意图 4.4.2基本方程假定倒摆由无质量的轻杆和质量为m的小球组成,小车的质量为M,系统所受的外力包括小球受到的重力和对小车水平方向的驱动力u(t)。x(t)和θ(t)分别表示小车的水平坐标和倒摆偏离垂直方向的角度,如图4.27所示。根据牛顿运动学第二定律,在水平x轴方向上系统满足下面的方程：(4.85) 图4.27小球受到的力矢量图 其中,小球受到的重力为常值,其中心的坐标表示为(xG,yG),满足xG=x+lsinθyG=lcosθ(4.86)l为倒摆的杆长。将式（4.86）代入式（4.85）,得到(4.87)由下面的基本关系(4.88)(4.89) 得到同样,通过小球的力矩平衡关系,可以得到小球的平衡方程：(4.90)(4.91)由式（4.86）～（4.89）,可以计算得到Fx和Fy的表达式:(4.92)(4.93) 将式（4.92）、（4.93）代入式（4.91）中,两边消去l：最后得到(4.94) 方程（4.90）和（4.94）构成了倒摆系统的动力学模型。显然,从数学的角度上看,该系统为明显的非线性系统。但是对小车施加驱动力的目的是保持倒摆在垂直方向上的姿态,因此,我们关注的是倒摆在垂直方向附近的动态变化,为此,可以将系统在该参考位置（θ=0）进行线性化,这样可以对简化得到的线性模型进行控制器的设计。在后面的内容中,将分别对线性化前后的模型进行比较和研究。 4.4.3非线性状态方程描述为了对倒摆系统的非线性模型进行数值仿真,需要首先将模型表示成标准的状态方程形式：由式（4.94）可以得到(4.95)(4.96)将其代入式（4.90）,有(4.97)(4.98) 将其代入式（4.90）中同样,可以由式（4.94）得到(4.99) 上式满足式（4.95）的标准状态方程的形式。假定系统输出为倒摆的角度和小车的x轴坐标,则系统的输出方程为(4.102) 4.4.4线性状态方程描述为了得到倒摆在垂直位置附近的线性化模型,我们只要对式（4.97）描述的非线性状态方程进行线性化即可。根据前几节论述的方法,该系统的线性化模型为(4.103) 这里的参考状态为倒摆静止在垂直方向,并且小车的驱动力为零,即Z0=0,u0=0。下面来逐项计算Jacobian矩阵。Jz(Z0,u0)的第一列由决定,其中第一和第三个函数与z1不直接相关,其偏导数等于零。对于第二项,有 同样,对第四项有 Jz(Z0,u0)的第二列由fi/z2|z0,u0决定,式(4.101)显示f1/z2=1,f3/z2=0,对于第二和第四项有Jz(Z0,u0)的第三和第四列中仅有的非零项为 4.4.5倒摆系统的MATLAB仿真1.倒摆系统的开环与闭环仿真这一部分的仿真主要研究下面三方面的内容：(1)对倒摆非线性模型与线性化模型不稳定动态特性的比较。(2)线性化模型可以由MATLAB函数linmod直接计算得到，以及如何用S函数表示非线性模型。(3)列举一些不够理想的经典反馈控制方案。 仿真计算的M文件包括INVPN1.M、INVPNNL1.M和INVPNNL2.M等等。其中,INVPN1.M为主文件,主要功能是控制仿真计算的流向同时完成以上的分析过程。第(1)步比较将检验倒摆线性化系统与非线性系统的阶跃响应。倒摆的非线性模型在INVPNNL1.M文件中进行定义,仿真采用MATLAB的ode23函数计算模型中状态变量的导数。 由于模型是不稳定的,因此只仿真系统1s内的动态行为,仿真结果如图4.28所示。从图中可以发现,随着小车水平指标的增长,倒摆将沿逆时针方向偏离垂直状态,这与实际经验相吻合。同时可以观察到,在仿真的最后,非线性模型与线性化后的模型动态行为的差异越来越大,这是因为对系统的线性化是在倒摆垂直方向（Z0=0）进行的,因此这种近似只是在该点附近有意义。 图4.28倒摆开环系统的阶跃响应 INVPN1.M文件的第(2)步将演示如何在MATLAB/Simulink环境中进行动态系统的仿真。在MATLAB仿真中,一个Simulink仿真方框图可以被转换成相应的S函数,该函数具备所有的仿真方程,可以用来计算状态变量的导数、输出函数以及系统的初始状态。随后,转换后的S函数可以用来进行仿真（使用sim命令）或者计算线性化模型（使用linmod）。在这个例子中,S函数直接在INVPNNL2.M文件中构造,它可以通过Simulink中的Sfunction模块连接到仿真方框图中。 尽管某些具体语法不同,但S函数文件INVPNNL2.M所包含的基本方程与ode23函数文件INVPNNL1.M中所使用的方程基本相同。有关S函数的使用说明请参考MATLAB/Simulink的有关文档和帮助（可以参考sfuntmpl模板文件）。在这个例子中,sim和linmod函数分别被用来仿真非线性系统的阶跃响应和计算参考点附近的线性模型。将其结果与前面MATLAB的标准分析结果相比较，可以发现二者是完全相同的。 这样,S函数可以用来替代MATLAB中传统的ODE求解器进行系统仿真,同时它还为用户带来更大的灵活性,尤其在希望对线性化模型进行数值分析的时候。在这个例子中,系统的线性化模型原本是由计算相应的Jacobian矩阵得到的,不难看出,这种过程是相当费时的,并且对于比较复杂的系统,这种计算甚至很难进行。借助Simulink中的linmod函数,可以采用数值方法很容易地得到系统的线性化模型。 上面的仿真结果显示倒摆的开环响应是不稳定的,因此需要设计控制器来镇定倒摆系统并且提高系统对外界的抗干扰能力。图4.29、4.30为倒摆设计了经典控制器。问题是倒摆的开环系统在原点有两个极点,另一个不稳定极点位于负平面的右半平面。我们希望同时控制小车的位置和倒摆的姿态,而系统只有对小车的驱动力一个输入变量。 图4.29倒摆姿态的经典控制方框图 图4.30小车位置的经典控制方框图 图4.31小车位置和倒摆姿态的经典控制方框图 图4.32经典控制器作用下倒摆系统的响应曲线 上面的仿真结果显示倒摆的开环响应是不稳定的,因此需要设计控制器来镇定倒摆系统并且提高系统对外界的抗干扰能力。图4.29、4.30为倒摆设计了经典控制器。问题是倒摆的开环系统在原点有两个极点,另一个不稳定极点位于负平面的右半平面。我们希望同时控制小车的位置和倒摆的姿态,而系统只有对小车的驱动力一个输入变量。 2.状态反馈的MATLAB仿真上面的仿真结果显示倒摆系统的经典控制器的控制效果不尽人意,因此下面将为它设计状态反馈控制器。INVPN2.M文件演示了针对倒摆系统的状态反馈控制器的仿真和设计过程。同时比较了在加入状态观测器和没有状态观测器情况下系统线性化模型的动态行为,并且为非线性模型设计了全状态观测器和状态反馈控制器。 INVPN2.M文件一开始为倒摆系统和线性化模型建立了基本的设计参数,确定闭环系统的根极点位于-1.5±3j、-5和-6,最后对小车位置的阶跃响应进行了仿真。下面分析在这样的根极点位置情况下系统的频域特性。 极点位置自然频率阻尼比最大超调量、上升时间和稳定时间 因此系统具有大约20%的超调量和3s的稳定时间,这样的动态系统应该是比较理想的。对于期望的闭环系统极点,MATLAB中的place函数可以决定期望的反馈增益。图4.33、4.34为小车位置和状态变量的仿真曲线。 图4.33状态反馈下小车位置的阶跃响应曲线 从仿真曲线中可以看出,系统的动态属性与期望的一致：小车开始沿x+方向移动,3～4s后静止在x=1m处。注意到这时候所有的状态变量都趋于0,x(t)趋于平衡点（如图4.34所示）。 图4.34状态反馈下状态变量的时间曲线 INVPN2.M文件的下一步是为闭环系统加入状态观测器,适当选择观测器的极点,使观测器的动态速度是系统的两倍以上。为此,再次使用MATLAB的place命令,从而确定观测器的增益。最后对带全观测器的状态反馈控制系统进行仿真,得到的结果与图4.34显示的一致。图4.35显示了系统状态与观测器得到的估计状态之间的误差曲线。显然,所设计的观测器是收敛的。 图4.35线性模型与观测器模型状态变量的误差曲线 为了检验状态反馈控制器的鲁棒性,INVPN2.M文件还对系统的非线性模型进行了相同的控制仿真。非线性控制系统的闭环仿真结果分别如图4.36～4.38所示。在这种情况下系统达到平衡点的过程要相对漫长一些。但总的来说,倒摆系统的阶跃响应是比较理想的,因此不需要重新设计控制器的参数。不过,既然这里的模型是非线性的,而观测器是线性的,我们看到的状态变量的误差与线性模型的情况相比要大一些。 图4.36非线性模型和线性观测器下小车位置的阶跃响应曲线 图4.38中所有的状态变量随时间变化都趋于零,但是除了小车位置,其它的状态误差与实际系统的状态具有相同的数量级（比较图4.35和图4.38）,从而直接影响到系统的动态性能（如图4.36所示）。尽管这种误差不可避免,不过由于它的幅值不大,因此倒摆闭环系统在整体上仍可以达到较为理想的动态性能。 图4.37非线性模型和线性观测器下的系统暂态响应 图4.38非线性模型和线性观测器下状态变量的误差曲线 3.扰动条件下系统的MATLAB仿真作为对倒摆系统最后的仿真演示,下面进一步考虑风对倒摆系统的干扰影响。假定FW表示风在水平方向上对倒摆系统的干扰作用,则式（4.85）表示的原始的系统动力学模型可改写成：从而有(4.107)(4.108) 水平风所引起的沿顺时针方向的力矩大小为(FWcosθ)l,将它加到式（4.91）中(4.109)(4.110)式（4.108）与（4.110）是考虑水平风干扰影响下的新的系统模型。这两个非线性方程可以按照前面讲述的方法写成标准的状态方程形式。基本步骤包括：（1）在力矩平衡方程中求解,将其代入力平衡方程中，得到 （2）在力矩平衡方程中求解,并代入力平衡方程中,得到 两边同时乘以cosθ，有最后得到状态方程描述为(4.111) 同样通过计算Jacobian矩阵,可以得到线性化的系统模型 式（4.112）是倒摆系统在小车水平驱动力δu(t)和水平风δFW作用下的开环线性化模型。相应的LTI系统模型具有如下的形式：(4.113)文件INVPN3.M对式（4.113）所描述的具有可变扰动输入的闭环系统进行了仿真。首先将风的大小设置为零,然后设计闭环反馈系统（不带状态观测器）,所得到的仿真结果与INVPN2.M文件中的仿真结果一致。注意到该系统属于标准的单输入单输出（SISO）的LTI系统,因此可以采用标准的方法验证系统的可控性并计算系统的反馈增益。 一旦完成状态控制器后,我们将它加入到仿真模型中。在这里我们定义另一个B矩阵（对应于INVPN3.M文件中的BB矩阵）,它同时包含式（4.113）中定义的b1和b2参数。还应该注意空矩阵D的维数重新进行了定义。系统的开环和闭环系统总结如下：开环系统(4.114)控制律(4.115)闭环系统(4.116) INVPN3.M文件针对系统（4.116）在四种情况下进行了仿真。第一种情况是风大小为零时参考点rd变化时的阶跃响应,其结果应该与INVPN2.M文件中的仿真结果一致（如图4.39所示）。 图4.39参考点位置变化时的阶跃响应曲线（无风） 第二种情况对干扰输入为0.2N的常值干扰情况下的闭环系统进行了仿真。仿真结果如图4.40所示。从图中曲线可以看到,由于风干扰的影响,小车位置存在0.65m左右的误差。这是因为为了保持倒摆始终位于垂直状态,需要对小车施加一定大小的力来抵消干扰的作用,从而使得小车偏向右边一定的距离。同时注意到,大小为+0.2N的常值风的干扰可以通过0.2N的小车力矩来补偿(图中为了同样的量程绘制输入力矩与干扰力矩,将干扰的作用放大了10倍)。 图4.40常值风干扰下的系统响应（参考点不变） 第三种情况是前两种情况的综合。既然系统是线性的,系统的行为将是两种情况输入的累加,这点从图4.41所示的仿真结果可以得到验证。从图中可以看出,系统稳态时的状态距离期望的单位值存在0.65左右的偏差。同时可以看出,小车位置、控制输入和扰动输入都是前两种情况的累加。 最后,我们观察随机噪声干扰下小车位置的动态仿真。由一个随机信号发生器产生均值为零的随机噪声作为系统的干扰信号,其幅值大小为±0.2N。图4.42显示了系统的仿真结果。从仿真曲线上看到,由于风的随机性干扰,小车位置在到达平衡点后仍保持一定的振荡。不过由于状态反馈控制器发挥的良好的控制作用,小车始终位于期望的参考点附近。在这个例子中,由于风的平均影响为零,因此系统平均的状态稳态误差也为零。 系统输入也表现出很高频率的随机性,以抵消随机风的干扰影响。从仿真结果上看,即使系统受到一定范围的可变风的干扰影响,所设计的状态控制器仍然可以对系统施加有效的控制,但是随着干扰信号幅值的增大,倒摆系统的综合性能也相应变差。 图4.41风干扰作用下系统的单位阶跃曲线（参考点变化） 图4.42随机风干扰影响下的系统阶跃响应曲线 4.4.6仿真程序源代码这一小节将列举倒摆系统仿真中用到的主要程序文件,读者可以仔细阅读具体代码,并结合前面讲述的内容,来进一步熟悉和掌握非线性系统设计和仿真的一般方法。%INVPN1.M倒摆系统仿真演示＃1%(倒摆系统的开环与闭环仿真)%相关文件：%invpnnl1.m-包含基本的非线性系统模型%invpnnl2.m-采用S函数编写的非线性系统模型%invpnsl.mdl-包含S函数模块的Simulink仿真模型 %invpnsl1.mdl-包含倒摆角度经典控制器的Simulink线性模型%invpnsl2.mdl-包含小车位置经典控制器的Simulink线性模型%invpnsl3.mdl-包含小车位置和倒摆角度经典控制器的Simulink线性模型clearall,closeall,nfig=0;deleteinvpn1.out%%打开二进制文件以保存结果diaryinvpn1.outdisp(′′)disp(′***INVPN1.OUT***DiaryFileforINVPN1.M′) disp(′′)%PartI.为非线性或线性化模型建立基本的数据,验证开环系统的不稳定性；比较非线性模型%与线性模型的阶跃响应曲线%基本数据globaluMmglen%在invpnnl1.M文件中使用的常量M=2.0;m=0.1;%小车与小球的质量(Kg)len=0.5;%倒摆的杆长g=9.81;%重力加速度 %输入力矩u=1时非线性系统的阶跃响应曲线u=1;to=0;tf=1.0;zo=［0000］′;tol=1.0e-6;options=odeset(′RelTol′,tol);［tnl1,znl1］=ode23(′invpnnl1′,［totf］,zo,options);%创建线性化模型的状态空间矩阵c1=M*len;c2=m*len;c3=m*g;c4=(M+m)*g;A1=［0100;c4/c1000;0001;-c3/M000］;B1=［0-1/c101/M］′;C1=［1000;0010］;D1=［00］′; disp(′StateSpaceMatricesfortheAnalyticallyDeterminedLinearModel′)A1,B1,C1,D1%计算状态矩阵的特征值disp(′Eigenvaluesofthe"AnalyticalLinearModel"′);ev=eig(A1)%确定线性化系统模型的阶跃响应tl=linspace(to,tf,31);sysl1=ss(A1,B1,C1,D1);［yl1,tl,zl1］=step(sysl1,tl) %比较非线性与线性模型的结果（开环）nfig=nfig+1;figure(nfig);subplot(2,1,1),plot(tnl1,znl1(:,1),′g-′,tl,zl1(:,1),′go′),gridtitle(′InvertedPendulumRodAngle(stepresponse)′)xlabel(′Time(sec)′),ylabel(′RodAngle(radians)′)legend(′nonlinear′,′linear′) %subplot(2,1,2),plot(tnl1,znl1(:,3),′r-′,tl,zl1(:,3),′ro′),gridtitle(′InvertedPendulumCartPosition(stepresponse)′)xlabel(′Time(sec)′),ylabel(′CartPosition(m)′)legend(′nonlinear′,′linear′) %PartII.使用S函数来描述非线性系统,使用Simulink中的sim函数来仿真非线性系统；%使用Simulink的linmod命令来计算系统在参考点处的线性化模型%当输入u=1时非线性系统的仿真曲线invpnsl%显示包含非线性S函数模型的Simulink模型ut=［tou;tfu］;options=simset(′RelTol′,tol);［tnl2,znl2,ynl2］=sim(′invpnsl′,［totf］,options,ut); %创建线性化模型的状态空间矩阵［A2,B2,C2,D2］=linmod(′invpnsl′,zo,0);disp(′StateSpaceMatricesfortheNumericallyDeterminedLinearModel′)A2,B2,C2,D2%计算状态矩阵的特征值disp(′Eigenvaluesofthe"NumericalLinearModel"′);ev=eig(A2) %确定线性系统的阶跃响应tl=linspace(to,tf,31);sysl2=ss(A2,B2,C2,D2);［yl2,tl,zl2］=step(sysl2,tl);%比较非线性模型与线性模型的仿真结果（无反馈）nfig=nfig+1;figure(nfig);subplot(2,1,1),plot(tnl2,znl2(:,1),′g-′,tl,zl2(:,1),′go′),gridtitle(′SFunInvertedPendulumRodAngle(stepresponse)′)xlabel(′Time(sec)′),ylabel(′RodAngle(radians)′)legend(′nonlinear′,′linear′) %subplot(2,1,2),plot(tnl2,znl2(:,3),′r-′,tl,zl2(:,3),′ro′),gridtitle(′S-FunInvertedPendulumCartPosition(stepresponse)′)xlabel(′Time(sec)′),ylabel(′CartPosition(m)′)legend(′nonlinear′,′linear′)%PartIII.设计最简单的经典控制器来稳定系统,针对小车位置的闭环系统进行仿真 %对在Simulink模型中使用的矩阵进行初始化A=A1;B=B1;C=C1;D=D1;%倒摆角度的反馈invpnsl1%显示相关Simulink仿真模型（倒摆角度反馈disp(′FollowingdataforRODPOSITIONfeedback:′);K1=［0.111010050010005000］;forj=1:7k1=-K1(j),［A1,B1,C1,D1］=linmod(′invpnsl1′);eig(A1)end %小车位置反馈invpnsl2%显示相关Simulink仿真模型（小车位置反馈）disp(′FollowingdataforCARTPOSITIONfeedback:′);K2=［0.111010050010005000］;forj=1:7k2=-K2(j),［A2,B2,C2,D2］=linmod(′invpnsl2′);eig(A2)end %同时加入两个反馈回路（小车位置与倒摆角度）invpnsl3%显示相关Simulink仿真模型（两个反馈回路disp(′Closedloopsystemwithtwofeedbackloops′);k1=-50,k2=-2%缺省的增益值nfig=nfig+1;cont=′y′;whilecont==′y′［A3,B3,C3,D3］=linmod(′invpnsl3′);eig(A3) %仿真系统的阶跃响应to=0;tf=10;tlf=linspace(to,tf,101);sysl3=ss(A3,B3,C3,D3);［ylf,tlf,zlf］=step(sysl3,tlf);figure(nfig);subplot(3,1,1),plot(tlf,ylf(:,1),′g-′),gridtitle(［′LinearInvertedPendulumBehavior(k1=′,...num2str(k1),′&k2=′,num2str(k2),′)′］)ylabel(′RodAngle(radians)′)%subplot(3,1,2),plot(tlf,ylf(:,2),′r-′),gridylabel(′CartPosition(m)′) %u=k1*ylf(:,1)+k2*(1-ylf(:,2));subplot(3,1,3),plot(tlf,u,′b-′),gridxlabel(′Time(sec)′),ylabel(′InputForce(N)′)%cont=input(′Selectdifferentgains?(y/n):′,′s′);ifisempty(cont);cont=′n′;endifcont==′y′disp(′Inputvaluesforgains(k1&k2)′)k1=input(′k1=′);k2=input(′k2=′);endend %%绘制仿真结果曲线nfig=nfig+1;figure(nfig);plot(tlf,ylf(:,1),′g-′),gridtitle(［′InvertedPendulumRodPosition(k1=′,...num2str(k1),′&k2=′,num2str(k2),′)′］)xlabel(′Time(sec)′),ylabel(′RodAngle(radians)′)%nfig=nfig+1;figure(nfig);plot(tlf,ylf(:,2),′r-′),gridtitle(［′InvertedPendulumCartPosition(k1=′,...num2str(k1),′&k2=′,num2str(k2),′)′］)xlabel(′Time(sec)′),ylabel(′CartPosition(m)′) %nfig=nfig+1;figure(nfig);plot(tlf,u,′b-′),gridtitle(［′InvertedPendulumInputForce(k1=′,...num2str(k1),′&k2=′,num2str(k2),′)′］)xlabel(′Time(sec)′),ylabel(′InputForce(N)′)diaryoff%关闭二进制文件disp(′Endofsimulation′)%仿真结束%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%INVPN2.M倒摆系统仿真演示＃2%对倒摆的状态反馈控制系统进行仿真（线性和非线性系统） %文件invpnnl3.M为系统的非线性模型clearall,closeall,nfig=0;globaluMmglenABCDKsNrLrd%定义在文件中使用的全局变量deleteinvpn2.out%打开二进制文件以保存结果diaryinvpn2.outdisp(′′)disp(′***INVPN2.OUT***DiaryFileforINVPN2.M′)disp(′′) %PartI.建立线性模型,显示倒摆系统是不稳定的M=2.0;m=0.1;%小车和末端小球的质量(Kg)len=.5;%倒摆的杆长(m)g=9.81;%重力加速度(m/s^2)%创建线性模型的状态方程c1=M*len;c2=m*len;c3=m*g;c4=(M+m)*g;A=［0100;c4/c1000;0001;-c3/M000］;B=［0-1/c101/M］′;C=［0010］;D=［0］; disp(′StateSpaceMatricesfortheLinearModel′)A,B,C,D%计算线性模型状态矩阵的特征值disp(′Eigenvaluesofthe"LinearModel"′);ev=eig(A)%PartII.加入状态反馈控制,仿真小车位置控制系统的阶跃响应%检查系统的完全可控性disp(′ControllabilityMatrixforthissystem′),CM=ctrb(A,B)disp(′RankofControllabilityMatrix′),rank(CM)clp=［-1.5+3.0j-1.5-3.0j-5.0-4.0］;%计算闭环系统的反馈增益 Ks=place(A,B,clp);disp(′Desiredclosedlooppolesforstatefeedbackcontroller′);clpdisp(′Statefeedbackgainsneededtogivedesiredpoles′);Ksdisp(′Calculatedeigenvaluesofsystemwithstatefeedback′);eig(A-B*Ks)Nr=-1.0/(C*inv(A-B*Ks)*B);%计算稳态误差disp(′SetpointgainforzeroSSerror′);Nrtto=0;ttf=5;t=linspace(tto,ttf,101);%仿真线性模型+控制器 syscl1=ss(A-B*Ks,B*Nr,C,D);［y1,t,x1］=step(syscl1,t);nfig=nfig+1;figure(nfig)%绘制状态反馈控制的相关结果plot(t,y1,′r-′),gridxlabel(′Time(sec)′),ylabel(′CartPosition(m)′)title(′InvertedPendulumwithStateControl(CartPosition)′)nfig=nfig+1;figure(nfig)subplot(4,1,1),plot(t,x1(:,1),′g-′),grid,ylabel(′Angle′)title(′StatesforInvertedPendulum(StateFeedback)′) subplot(4,1,2),plot(t,x1(:,2),′g′),grid,ylabel(′d(Angle)/dt′)subplot(4,1,3),plot(t,x1(:,3),′r-′),grid,ylabel(′Position′)subplot(4,1,4),plot(t,x1(:,4),′r-′),grid,ylabel(′d(Pos)/dt′)xlabel(′Time(sec)′)%PartIII.在反馈控制器的基础上加入全状态观测器,其仿真结果应与PartII相同%检查系统的完全可观性disp(′ObservabilityMatrixforthissystem′),OM=obsv(A,C)disp(′RankofObservabilityMatrix′),rank(OM) %计算指定极点的观测器增益op=2*clp;%观测器的速度是闭环系统的两倍L=place(A′,C′,op);L=L′;disp(′Desiredobserverpolesforstatefeedbackcontroller′);opdisp(′Estimatorgainsneededtogivedesiredpoles′);Ldisp(′Calculatedeigenvaluesofestimatorsystem′);eig(A-L*C) %创建线性模型+控制器系统A11=A;A12=-B*Ks;B1=B*Nr;A21=L*C;A22=A-L*C-B*Ks;B2=B*Nr;AB=［A11A12;A21A22］;BB=［B1;B2］;zz=0;CB=［Czz*C］;%仿真线性模型+控制器系统syscl2=ss(AB,BB,CB,D);［y2,t,x2］=step(syscl2,t);nn=max(size(A));%将系统状态与观测器状态分离xp2=x2(:,1:nn);xe2=x2(:,nn+1:2*nn); nfig=nfig+1;figure(nfig)%仿真全观测器的相关结果plot(t,y2,′r-′),gridxlabel(′Time(sec)′),ylabel(′CartPosition(m)′)title(［′InvertedPendulumwithStateControl&FullObserver。。。(CartPosition)′］)nfig=nfig+1;figure(nfig)subplot(4,1,1),plot(t,xp2(:,1),′g-′),grid,ylabel(′Angle′)title(［′StatesforInvertedPendulum(StateFeedback/FullObserver)′］) subplot(4,1,2),plot(t,xp2(:,2),′g′),grid,ylabel(′d(Angle)/dt′)subplot(4,1,3),plot(t,xp2(:,3),′r-′),grid,ylabel(′Position′)subplot(4,1,4),plot(t,xp2(:,4),′r′),grid,ylabel(′d(Pos)/d′)xlabel(′Time(sec)′)nfig=nfig+1;figure(nfig)%系统状态与估计状态之间的误差曲线subplot(4,1,1),plot(t,xp2(:,1)-xe2(:,1),′g-′),grid,ylabel(′Angle′) title(［′DifferenceBetweenPlantandObserverStates′］)subplot(4,1,2),plot(t,xp2(:,2)-xe2(:,2),′g-...′),grid,ylabel(′d(Angle)/dt′)subplot(4,1,3),plot(t,xp2(:,3)-xe2(:,3),′r-...′),grid,ylabel(′Position′)subplot(4,1,4),plot(t,xp2(:,4)-xe2(:,4),′r-...′),grid,ylabel(′d(Pos)/dt′)xlabel(′Time(sec)′) %PartIV.被控对象采用非线性模型,观测器使用线性模型,重复PartIII的计算%仿真系统模型+控制器rd=1;%小车位置的单位阶跃响应tt0=0;ttf=5;Zo=zeros(8,1);tol=1.0e-6;options=odeset(′RelTol′,tol);［tt,Z］=ode23(′invpnnl3′,［ttottf］,Zo,options);nn=max(size(A));%分离系统状态与观测器状态zp=Z(:,1:nn);ze=Z(:,nn+1:2*nn); %仿真具有全状态观测器的非线性模型nfig=nfig+1;figure(nfig)plot(tt,zp(:,3),′r-′),gridxlabel(′Time(sec)′),ylabel(′CartPosition(m)′)title(′NonlinearInvertedPendulumwithStateControl...&FullObserver(CartPosition)′)nfig=nfig+1;figure(nfig)subplot(4,1,1),plot(tt,zp(:,1),′g-′),grid,ylabel(′Angle′)title(′StatesforNonlinearInvertedPendulum(State...Feedback/FullObserver)′) subplot(4,1,2),plot(tt,zp(:,2),′g′),grid,ylabel(′d(Angle)/dt′)subplot(4,1,3),plot(tt,zp(:,3),′r′),grid,ylabel(′Position′)subplot(4,1,4),plot(tt,zp(:,4),′r′),grid,ylabel(′d(Pos)/dt′)xlabel(′Time(sec)′) %系统状态与观测器估计状态之间的误差曲线nfig=nfig+1;figure(nfig)subplot(4,1,1),plot(tt,zp(:,1)-ze(:,1),′g′),grid,ylabel(′Angle′)title(［′DifferenceBetweenNonlinearPlantandObserverStates′］)subplot(4,1,2),plot(tt,zp(:,2)-ze(:,2),′g-...′),grid,ylabel(′d(Angle)/dt′)subplot(4,1,3),plot(tt,zp(:,3)-ze(:,3),′r′),grid,ylabel(′Position′) subplot(4,1,4),plot(tt,zp(:,4)-ze(:,4),′r-′),grid,ylabel(′d(Pos)/dt′)xlabel(′Time(sec)′)%PartV.计算系统的传递函数并进行频域仿真,这里不考虑状态观测器%计算频率响应freqp=input(′Performfrequencydomainanalysis?(y/n)［n］:′,′s′);ifisempty(freqp);freqp=′n′;endiffreqp==′y′ nfig=nfig+1;figure(nfig)%绘制Bode图w=logspace(-1,2,100);bode(syscl1,w);title(′G(s)=X(s)/R(s)(CartPosition)′)disp(′′)disp(′Notethatthissystemisnonminimumphasebecauseofthezero′)disp(′intherightportionofthecomplexplane′)disp(′′) %将状态空间形式转换成传递函数形式disp(′′)disp(′G(s)forCartPosition(TransferFunctionform)′)［num1,den1］=tfdata(syscl1,′v′)printsys(num1,den1)disp(′′)%将状态空间形式转换成零极点-增益形式disp(′G(s)forCartPosition(Zero-Poleform)′)［z1,p1,k1］=zpkdata(syscl1,′v′)zpk(syscl1) disp(′′)%计算系统的阻尼比和自然频率disp(′Dampingandnaturalfrequenciesforclosedloopsystem′),damp(p1)nfig=nfig+1;figure(nfig)pzmap(syscl1),sgridtitle(′Pole-ZeroMapforClosedLoopSystem′)enddiaryoff%关闭二进制文件%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %INVPN3.M倒摆系统演示＃3(扰动输入)%该程序对扰动输入情况下的倒摆(线性模型)系统和状态反馈控制器进行仿真clearall,closeall,nfig=0;deleteinvpn3.out%打开二进制文件diaryinvpn3.outdisp(′′)disp(′***INVPN3.OUT***DiaryFileforINVPN3.M′)disp(′′)M=2.0;m=0.1; len=.5;g=9.81;%建立线性模型的状态空间方程c1=M*len;c2=m*len;c3=m*g;c4=(M+m)*g;A=［0100;c4/c1000;0001;-c3/M000］;B1=［0-1/c101/M］′;B2=［01/c200］′;C=［0010］;D=［0］;disp(′StateSpaceMatricesfortheLinearModel′)A,B1,B2,C %验证系统的完全可控性disp(′ControllabilityMatrixforthissystem′),CM=ctrb(A,B1)disp(′RankofControllabilityMatrix′),rank(CM)%计算状态反馈增益clp=［-1.5+3.0j-1.5-3.0j-5.0-4.0］;Ks=place(A,B1,clp);disp(′Desiredclosedlooppolesforstatefeedbackcontroller′);clpdisp(′Statefeedbackgainsneededtogivedesiredpoles′);Ksdisp(′Calculatedeigenvaluesofsystemwithstatefeedback′); eig(A-B1*Ks)Nr=-1.0/(C*inv(A-B1*Ks)*B1);disp(′SetpointgainforzeroSSerror′);Nr%仿真线性模型+控制器(也可以使用lsim函数)BB=［B1B2］;D=［00］;%两个输入和一个输出syscl=ss(A-B1*Ks,BB,C,D);%Case1:无扰动情况下小车位置的单位阶跃响应to=0;tf=5;Nt=101;t=linspace(to,tf,Nt)′;u1=zeros(size(t));%控制信号输入(初始化) rd=ones(size(t));%参考信号v1=zeros(size(t));%扰动输入w1=［Nr*rdv1］;［y1,t,x1］=lsim(syscl,w1,t);fori=1:Nt,u1(i)=Nr*rd(i)-Ks*x1(i,:)′;end%控制信号输入%绘制相关结果nfig=nfig+1;figure(nfig)subplot(2,1,1),plot(t,y1,′r-′),grid,ylabel(′CartPosition(m)′) title(′LinearInvertedPendulum(Case1:rd=1&v=0)′)subplot(2,1,2),plot(t,u1,′g--′,t,10*v1,′b-′),gridylabel(′Inputs(N)′),xlabel(′Time(sec)′)legend(′u(t)′,′10*v(t)′)%Case2:常值干扰(0.2N)情况下小车位置的仿真u2=zeros(size(t));%controlledinput(initialize)rd=zeros(size(t));%参考点不变v2=0.2*ones(size(t));%扰动输入(0.2N) w2=［Nr*rdv2］;［y2,t,x2］=lsim(syscl,w2,t);fori=1:Nt,u2(i)=Nr*rd(i)-Ks*x2(i,:)′;end%控制输入信号%绘制相关结果nfig=nfig+1;figure(nfig)subplot(2,1,1),plot(t,y2,′r-′),grid,ylabel(′CartPosition(m)′)title(′LinearInvertedPendulum(Case2:rd=0&v=0.2N)′) subplot(2,1,2),plot(t,u2,′g--′,t,10*v2,′b-′),gridylabel(′Inputs(N)′),xlabel(′Time(sec)′)legend(′u(t)′,′10*v(t)′)%Case3:常值干扰(0.2N)情况下小车位置的阶跃响应u3=zeros(size(t));%控制输入(初始化)rd=ones(size(t));%参考信号v3=0.2*ones(size(t));%扰动输入(0.2N)w3=［Nr*rdv3］;［y3,t,x3］=lsim(syscl,w3,t);fori=1:Nt,u3(i)=Nr*rd(i)-Ks*x3(i,:)′;end%控制信号输入 %绘制相关结果nfig=nfig+1;figure(nfig)subplot(2,1,1),plot(t,y3,′r-′),grid,ylabel(′CartPosition(m)′)title(′LinearInvertedPendulum(Case3:rd=1&v=0.2N)′)subplot(2,1,2),plot(t,u3,′g--′,t,10*v3,′b-′),gridylabel(′Inputs(N)′),xlabel(′Time(sec)′)legend(′u(t)′,′10*v(t)′) %Case4:随机扰动(+/-0.2N)下小车位置的阶跃响应u4=zeros(size(t));%控制输入(初始化)rd=ones(size(t));%参考信号的阶跃变化rn=rand(size(t));a=-0.2;b=0.2;v4=(b-a)*rn+a;%在+/-0.2N之间的均匀分布w4=［Nr*rdv4］;［y4,t,x4］=lsim(syscl,w4,t);fori=1:Nt,u4(i)=Nr*rd(i)-Ks*x4(i,:)′;end%控制信号输入 %绘制相关结果nfig=nfig+1;figure(nfig)subplot(2,1,1),plot(t,y4,′r′),grid,ylabel(′CartPosition(m)′)title(′LinearInvertedPendulum(Case4:rd=1&v=randomnoise...(+/-0.2N))′)subplot(2,1,2),plot(t,u4,′g--′,t,10*v4,′b-′),gridylabel(′Inputs(N)′),xlabel(′Time(sec)′)legend(′u(t)′,′10*v(t)′)diaryoff%关闭二进制文件 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%INVPNNL1.M倒摆系统的非线性模型(ODE函数文件格式)functionzdot=invpnnl1(t,z)globaluMmglenzdot=zeros(size(z));c1=(M+m);c2=m*len;c3=m*g;c4=(M+m)*len;c5=(M+m)*g;zdot(1)=z(2);top2=u*cos(z(1))-c5*sin(z(1))+c2*cos(z(1))*sin(z(1))*z(2)^2;zdot(2)=top2/(c2*cos(z(1))^2-c4); zdot(3)=z(4);top4=u+c2*sin(z(1))*z(2)^2-c3*cos(z(1))*sin(z(1));zdot(4)=top4/(c1-m*cos(z(1))^2);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%INVPNNL2.M倒摆系统的非线性模型(Simulink的S函数格式)function［zdot,zo］=invpnnl2(t,z,u,flag,M,m,g,len)%返回参数大小和初始条件ifflag==0,zdot=［402100］;zo=zeros(4,1); %返回连续状态的导数(列向量)elseifflag==1c1=(M+m);c2=m*len;c3=m*g;c4=(M+m)*len;c5=(M+m)*g;zdot(1)=z(2);top2=u*cos(z(1))-c5*sin(z(1))+c2*cos(z(1))*sin(z(1))*z(2)^2;zdot(2)=top2/(c2*cos(z(1))^2-c4);zdot(3)=z(4);top4=u+c2*sin(z(1))*z(2)^2-c3*cos(z(1))*sin(z(1));zdot(4)=top4/(c1-m*cos(z(1))^2);zdot=zdot′; %返回输出向量(列向量)elseifflag==3zdot(1)=z(1);zdot(2)=z(3);zdot=zdot′;elsezdot=［］;end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%INVPNNL3.M闭环系统(状态反馈控制器)的非线性模型functionZdot=invpnnl3(tt,Z)globaluMmglenABCDKsNrLrd %分离系统状态与估计状态nn=max(size(A));zp=Z(1:nn,1);ze=Z(nn+1:2*nn,1);%计算全状态的导数(系统状态与观测器状态)yp=C*zp;u=Nr*rd-Ks*ze;c1=(M+m);c2=m*len;c3=m*g;c4=(M+m)*len;c5=(M+m)*g;zpdot(1)=zp(2);top2=u*cos(zp(1))-c5*sin(zp(1))+c2*cos(zp(1))*sin(zp(1))*zp(2)^2; zpdot(2)=top2/(c2*cos(zp(1))^2-c4);zpdot(3)=zp(4);top4=u+c2*sin(zp(1))*zp(2)^2-c3*cos(zp(1))*sin(zp(1));zpdot(4)=top4/(c1-m*cos(zp(1))^2);zedot=A*ze+L*(yp-C*ze)+B*u;%得到系统的全状态向量Zdot=［zpdot′;zedot］; 气管插管的护理ICU徐伟丽 正常的呼吸功能通畅的气道足够的呼吸驱动力神经肌肉反应能力完整的胸廓解剖结构正常的肺实质咳嗽、叹气和防止误吸的能力 气管插管的作用为防止肺误吸提供相对的保护维持气体交换所需的通畅气道提供肺与呼吸机连接的途径建立清除分泌物的通路 插管方法经口经鼻纤维喉镜喉罩 经口插管优点：直视插管，医生最熟悉，操作简单，设备要求少缺点：下颌和颈部必须有足够活动性才能保证直视，需要表面、局部或全身麻醉 经鼻插管优点：头部可保持正中位，无须麻醉，可依靠呼吸音引导非直视插管。当经口插管困难或不可能时（张口受限），可进行。鼻导管不影响下颌骨或口咽部修补手术缺点：快速插管困难。忙插时必须存在自主呼吸引导。直视插管与经口有相同缺点。插管过程易发生出血。留置插管中，鼻咽部可能变软打折。常并发鼻窦炎和耳炎 气管插管型号根据患者年龄、体型及插管适应证选择经口插管：女性7.0mm男性8.0mm经鼻插管：女性6.0-6.5mm男性7.0-7.5mm 气管插管深度经口：气管插管尖端至上切牙的距离，女性21cm，男性23cm经鼻：从鼻孔开始计算，女性26cm，男性28cm拍摄胸片：插管远端应位于主气管中间，成人应在隆突上约5cm 气管插管的固定胶布:注意唇周皮肤寸带:注意颈后皮肤经口插管每日变换位置，以防压迫致皮肤溃疡，躁动患者应用牙垫更需注意 气管插管患者的护理呼吸道管理预防感染神智观察呼吸机报警的检测胃肠道观察皮肤护理心理护理 呼吸道管理有效吸痰加强肺部物理治疗气囊的管理合理湿化 有效吸痰吸痰动作应轻稳准快，一次吸痰时间不超过15s，以免发生低氧血症吸痰前后吸纯氧3min，负压33.0-53.1kpa吸痰过程观察患者心律、心率、血压、血氧饱和度等参数的变化，观察痰液的性质和量、黏稠度危重患者和分泌物多的患者，吸痰时不宜一次吸净，应吸痰吸氧交替进行 有效吸痰痰黏稠不易吸出者，吸痰前可予生理盐水2～5ml冲洗气道，待几次通气后立即吸痰。吸痰管的外径不超过气管插管内径的1/2吸痰管插入深度以气管插管或气管切开套管长度再延长1cm为宜。过长易损伤气管黏膜，过浅不能吸净气道分泌物造成管端痰痂阻塞。 肺部物理治疗插管镇静患者的呼吸道纤毛运动消失，肺的自洁能力降低，肺部分泌物不能及时排出，且由于长期卧床，增加了呼吸道阻塞和肺部感染的机会。 肺部物理治疗气管插管病人应加强翻身拍背，每2h翻身叩背1次，使小支气管内痰液由于叩背的震动而松动进入较大支气管，易于排出。叩背时，五指并拢，掌指关节微屈，双手应之下而上，从边缘到中央，中等力量有节律拍打 气囊的管理气囊：18~25mmHg。主要作用是防止上呼吸道分泌物坠积和防止机械通气时漏气，同时对维持气切管的位置也起到了一定的作用(不是主要作用)。 气囊的管理气囊压力测定手捏气囊感觉法：比鼻尖软比口唇硬/硬度如耳廓（感觉差异）最小漏气技术充气：充气直到恰好呼吸时听诊不能闻及气囊周围漏气为止，再从气囊内抽出0.2—0.3ml气体气囊压力表：准确 气囊的管理常规检测气囊压力：每4小时检测一次鼻饲前交接班时定时放气——不推荐 合理湿化气管插管破坏了呼吸道正常的生理模式和防御功能，使过滤功能、加温湿化功能、纤毛运动功能丧失，因而有效的气道湿化非常重要。 合理湿化湿化方法持续滴注:微量泵4-8ml/h间隔滴注：每隔10-30min滴入0.5～lmL雾化吸入呼吸机湿化器（最好）人工鼻 呼吸机湿化器湿化器温度设置在32-35℃，气体相对湿度在95％左右，以维持支气管纤毛运动的最佳状态。同时室温保持在20-22℃，湿度为60％一7O％。避免寒冷、干燥的气体对呼吸道黏膜的刺激。呼吸机管道内产生的冷凝水要及时倾倒，避免逆流入呼吸道内引起感染。湿化器内及时添加蒸馏水，避免烧干，湿化器内不能使用生理盐水和药物，以免沉积影响加热。 合理湿化湿化液：无菌蒸溜水和0.45％盐水湿化液的量与温度：24h总量约200mL湿化液的温度保持在32-35℃ 合理湿化湿化原则：以痰液稀簿，能顺利吸引出或咳出；套管内无痰栓；听诊气管内无干鸣音或大量痰鸣音，呼吸通畅。 预防感染严格无菌操作防止误吸口腔护理消毒隔离 防止误吸抬高床头15～30度；鼻饲时应抬高30～45度鼻饲中及鼻饲后30－60min内尽量不吸痰及变换体位，以免刺激引起呕吐、误吸。鼻饲食物的量每餐不宜过多，200～300ml为宜，速度不宜过快，以15～30min喂完为宜，温度在38～40℃，以免冷热刺激而导致胃痉挛造成呕吐误吸。每次鼻饲前确定胃管是否在胃内，以防误灌。 口腔护理经口气管插管的患者，因口腔内插管及牙垫占据口腔大部分空间，以及胶布的纵横固定，口腔护理困难。细菌在口腔内迅速繁殖，特别是口腔损伤或口腔分泌物血性时，极易导致口腔感染及下呼吸道感染，这也是呼吸机相关性肺炎(VAP)的重要致病原因之一。 口腔护理口腔冲洗可彻底清洁口腔，根据病情2-6小时进行一次。冲洗液可根据口腔pH值进行选择一般患者用生理盐水或洗必泰口腔有出血或化脓时，用1.5％的过氧化氢长期大量应用抗生素者，选用3％的碳酸氢钠，抑制真菌的生长 口腔护理冲洗方法：一般在患者鼻饲前、扣背后，彻底吸净气管内及口腔内分泌物，床头抬高45度，保证气囊充盈，患者头偏向一侧，口角向下。除去固定气管插管的胶布，1名护士用手固定好气管插管，检查门齿处刻度并记录。移开牙垫，用去针头的2Oml注射器吸取冲洗液，从上口角向下方向对患者的牙齿、舌面及颊部、咽部颚部进行冲洗，另一名护士从下方口角插入吸痰管吸出口腔内液体，如此反复进行直至口腔清洁，用干棉球擦拭口腔 消毒隔离每日更换湿化溶液每周更换呼吸机螺纹管每周更换呼吸机管道定期做呼吸机管道细菌培养通风，减少人员流动 神志观察患者烦躁不安，口唇末梢发绀，说明缺氧轻度缺氧表现为烦躁中度缺氧表现为谵妄重度可引起昏迷 呼吸机管道管理防止牵拉打折不可直接置于患者肩部冷凝水收集器保持最低位置湿化加温线感应端保持高位 呼吸机报警监测与处理气道高压报警呼吸道分泌物过多气道痉挛积水过多管路受压、打折气道内痰或异物堵塞患者激动、烦躁气道低压报警气囊漏气、充气不足或破裂呼吸机管路破裂、断开或连接不紧气源不足致通气量下降设置参数不合适 胃肠道观察胃肠胀气：气囊漏气致咽部，进入胃内。常规放置胃管，定时抽吸。气管插管气囊定时充气长期应用呼吸机患者鼻饲，观察有无消化不良 皮肤护理使用镇静剂的患者尽可能避免不必要的刺激，减少大翻身次数，翻身时幅度不宜过大；每2h给患者翻身更换体位1次，肢体保持功能位，定时放松约束带，每班检查皮肤情况。定时帮患者局部按摩，使用气垫床，减轻局部受压，防止剪切力，保持床单整洁干净，预防压疮。 心理护理气管插管导致语言表达障碍，生活不能自理，家属不在身边，均会产生不良情绪。据调查ICU患者70％存在焦虑，50％经历躁动。在患者清醒期间，虽然患者还不能说话，但却能听到医护人员的说话，护士应加强与患者沟通，安慰患者，讲解各种插管、仪器、操作的重要性、必要性，取得患者配合。另可握住患者的手或抚摸患者额头，让患者感到安静及安全，在身心给予其支持，以减轻患者的焦虑和不适。护士应仔细观察患者的非语言行为表现，判断患者的需求；并教会其用非语言沟通技巧，如眼神、手势、点头示意、书写等，缓解不良情绪，使患者主动配合治疗和护理 谢谢'